POJ 1228 Grandpa's Estate
分析:给你一些点,这些点都在凸包的边或顶点上,问你凸包是不是稳定的,稳定凸包就是每条边上都至少有3个点,否则再多加一个点能形成更大的凸包,如果一条边上有>=3个点,这样在多加一个点,虽然也可能会形成更大的凸包,但一定不满足所有点都在边上,所以每条边都应该至少有3个点才稳定。用Graham扫描法求凸包时,会将除最左下角的点外其余的点排序,排序的规则是按照其余点和最左下角的连线和x轴所形成的角度排序的,角度小的排在前面,如果角度相同则将距离最左下角的点近的排在前面。这题已经已知所有点都在凸包上,所以排序之后点是这样的: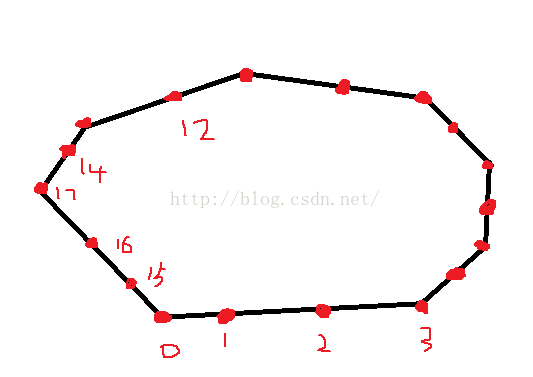 除了最后一条边外,其余顶点都是按逆时针顺序依次连接的,所有只要把最后一条边的顶点的次序调换一下,调换完之后完全是按逆时针排序了,然后在判断每条边上是不是有>=3个点就行了,要注意的是,输入的n可能小于6,最小的稳定凸包的顶点数是6个,就是三角形每条边3个点,所以n<6直接输出NO。
除了最后一条边外,其余顶点都是按逆时针顺序依次连接的,所有只要把最后一条边的顶点的次序调换一下,调换完之后完全是按逆时针排序了,然后在判断每条边上是不是有>=3个点就行了,要注意的是,输入的n可能小于6,最小的稳定凸包的顶点数是6个,就是三角形每条边3个点,所以n<6直接输出NO。
# include <stdio.h>
# include <math.h>
# include <algorithm>
using namespace std;
struct point
{
int x,y;
}v[1005];
void Swap(point &a,point &b)
{
point t;
t=a; a=b; b=t;
}
double Cross(point a,point b,point c)
{
return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y);
}
double Dis(point a,point b)
{
return sqrt((double)((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)));
}
int Middle(point a,point b,point c)
{
if((b.x-a.x)*(b.x-c.x)>0||(b.y-a.y)*(b.y-c.y)>0)
return 0;
return 1;
}
int cmp(point a,point b)
{
double t=Cross(v[0],a,b);
if(t!=0)
return t>0?1:0;
return Dis(v[0],a)<Dis(v[0],b);
}
int main()
{
int i,j,n,min,t,f;
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
for(i=0,min=0;i<n;i++)
{
scanf("%d%d",&v[i].x,&v[i].y);
if(v[i].y<v[min].y||(v[i].y==v[min].y&&v[i].x<v[min].x))
min=i;
}
if(n<6)
{printf("NO\n");continue;}
Swap(v[0],v[min]);
sort(v+1,v+n,cmp);
for(i=0;i<n;i++)
if(Cross(v[i],v[i+1],v[i+2])<0)
break;
for(i=i+1,j=0;i+j<n-1-j;j++)
Swap(v[i+j],v[n-1-j]);
for(i=0,f=0;i<n;i++)
{
if(Cross(v[i],v[(i+1)%n],v[(i+2)%n])==0&&Middle(v[i],v[(i+1)%n],v[(i+2)%n])==1)
f=1;
else if(f==0)
break;
else
f=0;
}
if(i<n)
printf("NO\n");
else
printf("YES\n");
}
return 0;
}