ZOJ1074

题目链接：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemId=74

可以肯定，直接暴力枚举各个矩形并计算和的话复杂度是O(n^6)，肯定会超时。

首先可以用一对对角来表示一个子矩阵（左上角和右下角，或者右上角和左下角），这里用左上角和右下角来表示。假设矩阵的左上角都是[1][1]。

用sum[i][j]表示从[1][1]到[i][j]的矩阵的和，那么假设要求从[i][j]到[k][l]的矩阵的和，那么所求结果就是sum[k][l]-sum[i-1][l]-sum[k][j-1]+sum[i-1][j-1].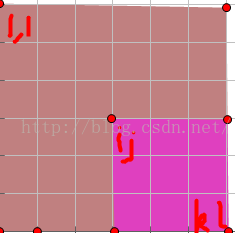

（数组sum的计算与之类似，看代码可以推理出来。）

这样复杂度是O(n^4)，两秒的时间够用了。但是这道题曾作为高中信息奥赛题目，时间限制是1秒，这个复杂度是不能够接受的，还需要继续优化。

回想一下最大连续子序列和，对于每一个数都有两个选择，要么接在前一个数所在的子区间的后面，要么单独作为一个新的子区间的开始，二者取其优。

那么对于一个矩阵，如果枚举正方形中的两个竖列，把两个竖列中的每一行都对应加起来，这样会得到一个和竖列，对这个竖列进行最大连续子序列和的话，得到的最大连续子序列实际上就是所枚举的两个竖列之间对应的一个最大子矩阵。当枚举玩所有的竖列，每一对竖列都进行所谓的最大连续子序列和，最终就会的到一个最大的子矩阵和，复杂度O(n^3)，1秒内没问题。

#include<iostream>
using namespace std;

int sum[110][110];
int a[110][110];

int main()
{
    int n;

    cin>>n;
    for (int i=1; i<=n; i++)
        for (int j=1; j<=n; j++) cin>>a[i][j];

    for (int i=1; i<=n; i++)
        for (int j=1; j<=n; j++)
            sum[i][j] = sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j];

    int ans = (1<<31);
    for (int i=1; i<=n; i++)
        for (int j=i; j<=n; j++)
    {
        int tmp = 1<<31;
        for (int k=1; k<=n; k++)
        {
            tmp = max(tmp,0) + sum[k][j]-sum[k-1][j]-sum[k][i-1]+sum[k-1][i-1];
            ans = tmp > ans ? tmp : ans;
        }
    }
    cout<<ans<<endl;

    return 0;
}