凸包问题 —— Graham扫描法
(1)找出点集p[]中最左下的点p1,把p1同点集中其他各点用线段连接,并计算这些线段与水平线的夹角,然后按夹角从小到大和按到p1的距离从近到远排序(夹角范围为 [0, 180)度,而且可以删除相同夹角且距离p1较近的点,保留最远点,这样可减少计算量。因为直线上的非端点不是凸包的极点,即如果p1,p2,p3在一条直线上,则只取凸点p1,p3。p2不在端点,故可以去掉),得到新的节点序列p1,p2,...pn.依次连接这些点,得到一个多边形(已经逆时针,有所进展,但还需去掉不在凸包上的点)。此时p1是凸包的边界起点,p2和pn也是最终凸包的顶点,p[n+1]=p1(看成循环的)
(2)删除p3,p4,...p[n-1]中不在凸包上的点:
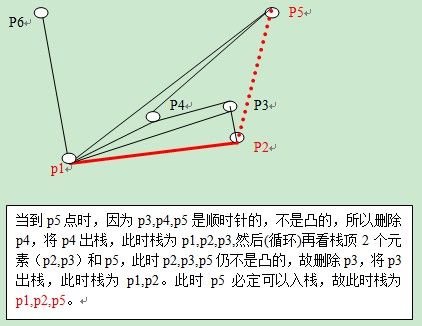
先把p1,p2,p3入栈S中,再依次循环(i = 3 -> n-1),若栈顶的两个点和当前的点p[i]这三点连线的方向向顺时针方向偏转,表明是凹的,应删除,则栈顶元素出栈(要循环判断,即可能前面的仍是凹的,还需再出栈,举例如下图),直到向逆时针方向偏转或者栈内只有2个元素了(p1p2),就把当前点p[i]入栈。
最后栈中的元素就是最终凸包上的点。
分析:一般会从最左下点p1开始,根据所有点斜率中最小的求下一个凸包点pa,再根据pa的所有点斜率中最小的来求下一个凸包点pb,依此类推,但这样就是三重循环(p1,pa,pb是一次,p1,pa,pb内部的排序有2次,共三重循环),这样效率不高(其实这就是卷包裹法,复杂度为O(NH),其中N是全部的点数 H是最终在凸包上的点数)。Graham扫描法只取所有点对p1的斜率,后面的点充分利用该斜率的信息,并作某些处理,进行改进,以提高效率。这是由多到少,由多个到1个的方法,并充分利用已知条件。
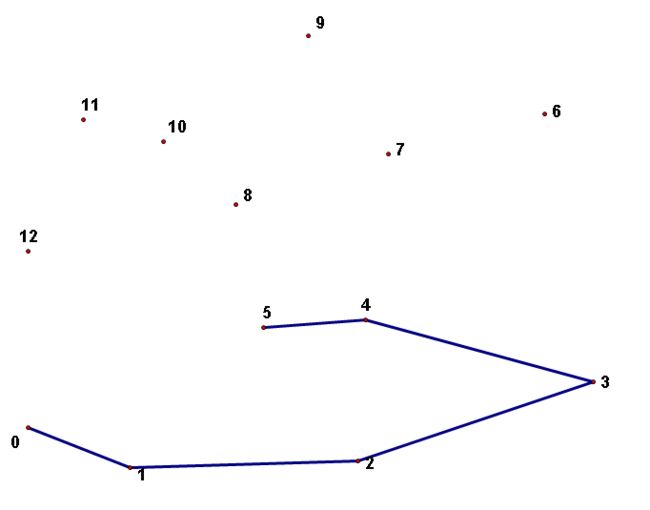
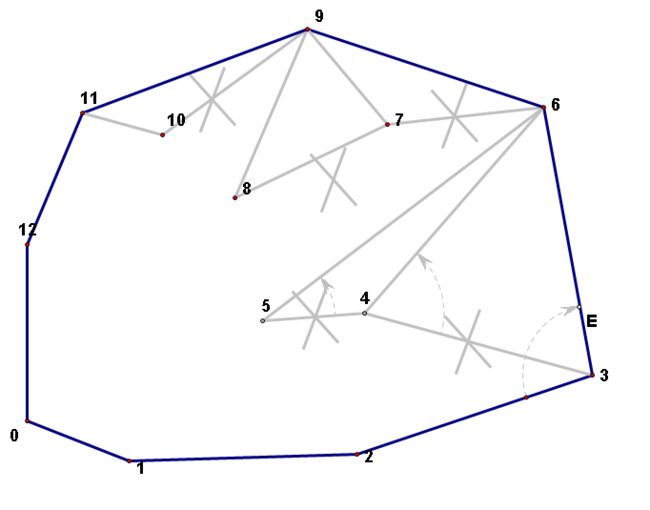
下面图例也可说明栈扫描的过程(摘自http://www.cnblogs.com/Booble/archive/2011/03/10/1980089.html#2065991):
----------------
---------------
--------------------
以下截图代码摘自《ACM程序设计培训教程 吴昊 中国铁道出版社》 :
―――――――――――
下面为网上转载:
对于一个有三个或以上点的点集Q,Graham扫描法的过程如下:
令p0为Q中Y-X坐标排序下最小的点
设<p1,p2,...pm>为对其余点按以p0为中心的极角逆时针排序所得的点集(如果有多个点有相同的极角,除了距p0最远的点外全部移除
压p0进栈S
压p1进栈S
压p2进栈S
for i ← 3 to m
do while 由S的栈顶元素的下一个元素、S的栈顶元素以及pi构成的折线段不拐向左侧
对S弹栈
压pi进栈S
return S;
若计算周长。将边相加 zoj1453
若计算面积。穷举三点构成的三角形。。找最大zoj2419
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define MaxNode 100015
int stack[MaxNode];
int top;
typedef struct POINT
{
int x;
int y;
}POINT;
POINT point[MaxNode];
void swap(POINT point[],int i,int j)
{
POINT tmp;
tmp=point[i];
point[i]=point[j];
point[j]=tmp;
}
double multi(POINT p1,POINT p2,POINT p0) //叉乘
{
return ((p1.x-p0.x)*(p2.y-p0.y)-(p1.y-p0.y)*(p2.x-p0.x));
}
double distence(POINT p1,POINT p2) //p1,p2的距离
{
return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
}
int cmp(const void *a,const void *b)
{
POINT *c=(POINT *)a;
POINT *d=(POINT *)b;
double k=multi(*c,*d,point[0]);
if(k<0) return 1;
else if(k==0&&distence(*c,point[0])>=distence(*d,point[0])) return 1; //极角相同,比距离
else return -1;
}
void grahamscan(int n)
{
int i,u;
u=0;
for(i = 1;i<= n-1;i++) //找到最左下的点p0
if((point[i].y < point[u].y)||(point[i].y==point[u].y&&point[i].x < point[u].x))
u=i;
swap(point,0,u);
qsort(point+1,n-1,sizeof(point[0]),cmp); //按极角排序
for(i = 0;i <= 2;i++) stack[i] = i; //p0,p1,p2入栈
top=2;
for(i = 3;i <= n-1;i++) //最终凸包的各顶点的编号依次存在stack[]中。
{
while(multi(point[i],point[stack[top]],point[stack[top-1]])>=0) //弹出非左转的点
{
if(top==0)break;
top--;
}
top++;
stack[top] = i;
}
}
//求凸包的面积
double polygonArea(int n,POINT p[])
{
double area;
int i;
area = 0;
for(i = 1;i <= n;i++){
area += (p[stack[i - 1]].x * p[stack[i % n]].y - p[stack[i % n]].x * p[stack[i - 1]].y);
}
return fabs(area) / 2;
}
int main()
{
int i;
for(i=0;i<10;i++)
scanf("%d%d",&(point[i].x),&(point[i].y));
grahamscan(10);
printf("%lf\n",polygonArea(10,point));
}