HDU 5476 Explore Track of Point

题意：给你3个点A,B,C的坐标，其中AB=AC，M为BC的中心，三角形内有一点P，让你求P的轨迹的长度，使得min{∠MPB+∠APC,∠MPC+∠APB}最大。

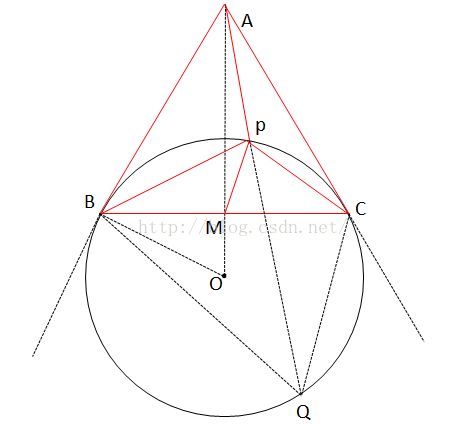
当P在以BC为底的△ABC的高上时，必有∠MPB+∠APC=∠MPC+∠APB=180°，所以P的轨迹长度之一为△ABC的高h.现在就是求P的其它的轨迹长度，使∠MPB+∠APC=∠MPC+∠APB=180°。

作⊙O，使得BC为⊙O的弦，AB,AC与⊙O相切，这样必有∠MPB+∠APC=∠MPC+∠APB=180°。

证明：

由弦切角定理（后面证明）可得：∠ACP=∠AQC,又∵∠A为公共角，∴△ACQ~△APC, ∴CQ/PC=AQ/AC

同理可得：∠ABP=∠AQB,有∵∠B为公共角，∴△ABQ~△APC,∴BQ/PB=AQ/AB

又∵AB=AC  ,∴CQ/PC=BQ/PB   ，∴BQ*PC=CQ*PB

由托勒密定理（后面证明）得：BC*PQ=BQ*PC+CQ*BP

∴2*BM*PQ=2*CQ*BP   ,  ∴ BM*PQ=CQ*BP

∴BM/CQ=BP/PQ         ,又∵∠PBC=∠PQC     ∴△PBM~△PQC

∴∠BPM=∠QPC           ∠BPM+∠APC=180°

∴在劣弧BC满足∠MPB+∠APC=∠MPC+∠APB=180°，为P的轨迹。

 

所以答案=以BC为底的△ABC的高+劣弧BC的长

 

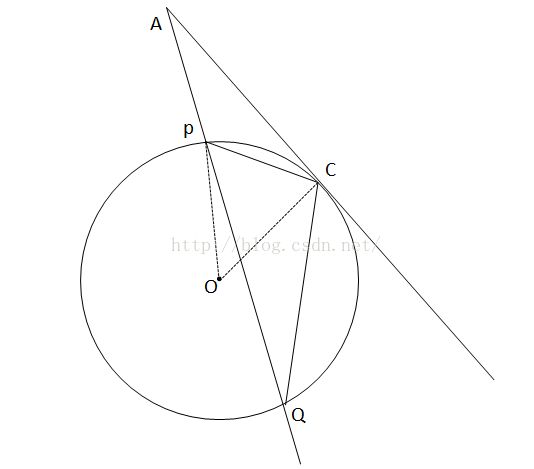
弦切角定理：弦切角的度数等于它所夹的弧所对的圆心角度数的一半。等于它所夹的弧的圆周角度数。

如图：AC是⊙O的切线，PQ为⊙O的弦，∴弦切角∠ACP=∠PQC=1/2∠COP

证明：由图可知：OP=OC     ∴∠OPC=∠OCP=1/2(180°-∠POC)=91°-∠AQC

∴∠AQC=90°-∠OCP=∠ACP

 

 

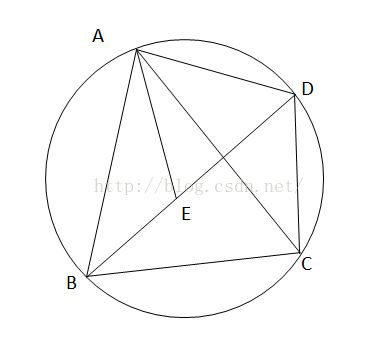
托勒密定理：如图A,B,C,D四点共圆，则AC*BD=AB*CD+AD*BC

证明：以AB为边，作一个角等于已知角，即∠BAE=∠DAC

在△ABE和△ACD中   ∵∠BAE=∠DAC    ∠ABE=∠ACD  ∴△ABE~△ACD   ∴AB*DC=BE*AC

∵∠BAE=∠DAC       ∴∠DAE=∠CAB

在△ADE和△ACB中   ∵∠ADE=∠ACB    ∠DAE=∠CAB  ∴△ADE~△ACB   ∴AD*BC=DE*AC

∴ AB*DC+AD*BC=BE*AC+DE*AC     ∴ AB*DC+AD*BC=BD*AC

 

# include <stdio.h>
# include <math.h>
  int main()
  {
      int i,t=1,T;
      double ax,ay,bx,by,cx,cy,t1,t2,ab,bc,h,d,angle,ans;
      scanf("%d",&T);
      while(T--)
      {
          scanf("%lf%lf%lf%lf%lf%lf",&ax,&ay,&bx,&by,&cx,&cy);
          t1=(ax-bx)*(ax-bx)+(ay-by)*(ay-by);
          ab=sqrt(t1);
          t2=(cx-bx)*(cx-bx)+(cy-by)*(cy-by);
          bc=sqrt(t2);
          h=sqrt(t1-t2/4);
          angle=acos(bc/(2*ab));
          d=bc/sin(angle);
          ans=d*angle+h;
          printf("Case #%d: %.4f\n",t++,ans);
      }
      return 0;
  }