xmu 1125 - 越野车大赛(三分)

题意：

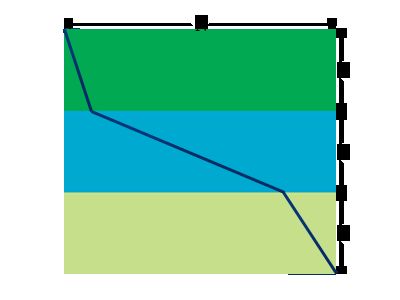
TheBeet正在参加一场越野车大赛。比赛的场地如右图：
　　共分三块，每一块地面的长宽均为N与M，但地表情况不同，越野车在这段路面上的最高速度也不同。
　　蓝色线表示TheBeet可能的行车路线。
　　比赛的要求是要求选手从比赛的场地左上角驾车至右下角。TheBeet想知道如果他在所有路段都以最快速度行驶（不考虑加速阶段），最快能在多少时间内完成比赛。

把 横向的边放到X轴上，设第一拐点距起点为x，第二个拐点距第一个拐点的距离为y，则方程很容易的便列出，

f(x,y) =sqrt(x*x+M*M)/S1+sqrt(y*y+M*M)/S2+sqrt((N-x-y)*(N-x-y)+M*M)/S3;

我们 很容易的便可以发现这是x和y的二次函数，且x和y的二次项的系数都是大于0的，

所以，它的函数曲线是下凸的，所以我们用两层的三分便可以求解得答案了。

代码如下：

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <queue>
#include <stack>
#include <list>
#include <vector>
#include <map>
#include <algorithm>

#define INF 0x7fffffff
#define eps 1e-7

using namespace std;

int m, n, s1, s2, s3;
double calcu(double x, double y)
{
    return sqrt(m*m+x*x)/s1+sqrt(m*m+y*y)/s2+sqrt((n-x-y)*(n-x-y)+m*m)/s3;
}
int main()
{
    scanf("%d%d%d%d%d", &n, &m, &s1, &s2, &s3);
    double L = 0, R = n;
    double mid, midmid, t1, t2;
    double LL, RR;
    double mid_, midmid_, tt1, tt2;
    double ans = 1e30;
    while(R-L>eps)
    {
        mid = (L+R)/2;
        midmid = (mid+R)/2;
        LL = 0, RR = n;
        while(RR-LL>eps)
        {
            mid_ = (LL+RR)/2;
            midmid_ = (mid_+RR)/2;
            tt1 = calcu(mid,mid_);
            tt2 = calcu(mid,midmid_);
            if(tt1<tt2) RR = midmid_;
            else LL = mid_;
        }
        t1 = calcu(mid, LL);
        LL = 0; RR = n;
        while(RR-LL>eps)
        {
            mid_ = (LL+RR)/2;
            midmid_ = (mid_+RR)/2;
            tt1 = calcu(midmid,mid_);
            tt2 = calcu(midmid,midmid_);
            if(tt1<tt2) RR = midmid_;
            else LL = mid_;
        }
        t2 = calcu(midmid, LL);
        if(t1<t2) { R = midmid; ans = min(ans, t1); }
        else  { L = mid; ans = min(ans, t2); }
    }
    printf("%.10lf\n",ans);
    return 0;
}