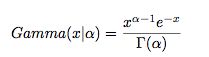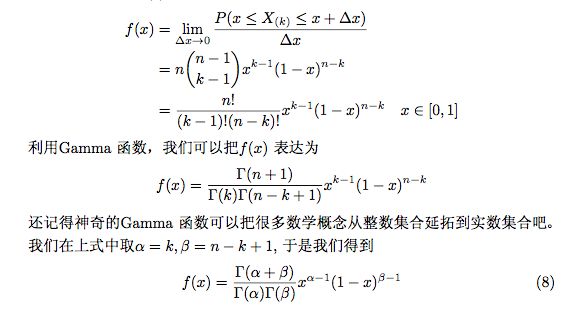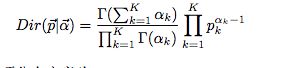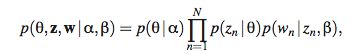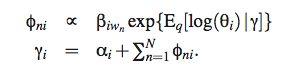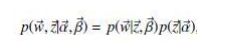lda 原理以及变形
1.为什么要使用lda?
我们简单来看一些其他的一些算法
(1) tf-idf
这种方法给一篇文章提取一些有 代表性的词 来代表文章,tf是词频,idf是词的区分力(如果一个文章中包含一个词,其它文章包含的少可说明词有比较好的区分力度)。 这种方法是词向量的一种方法。 但是如果有两个文章分别是 “乔布斯离我们远去了” “苹果手机卖的很好” 用这种方法提取关键词,并不能找出二者的关联。
(2) lsi / lsa
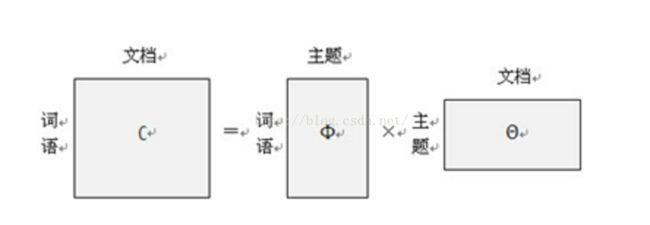
通过中间变量topic 来将 词对应到topic, 可以使原来的稀疏矩阵 降维到topic的矩阵上去。 缺点在于 解释性太差, 纯粹的数学方法;不能解决一词多意的问题,无法将文章中的词联系起来。
(3)plsa
相比lsa 引入了概率模型,通过期望最大化学习两个概率分布。 pLSA的参数个数是cd+wc 随着文档的参数的增加 参数个数线性增长,当数据量足够小的时候 会出现过拟合的现象,并且plsa 只是对当前的语料库建模 对未知的文章没有很好的预测能力,因为缺少先验。
2.狄利克雷分布
(1) gamma 函数 和 gamma分布
gamma 函数 是哥德巴赫 提出的问题: 如何求分数阶乘,最终高斯给出了公式:
通过分布积分法可以推到出如下的递归性质:
从而可以得到:
gamma 函数也可以应用到 求分数阶导数上面:
gamma 函数经过变形如下:
取积分中的函数作为概率密度,就得到 一个形式最简单的gamma 分布:
令 x = βt ,
α 决定分布的曲线, β 决定曲线有多陡。
gamma 能拟合各种分布形态, 所以gamma 分布作为先验非常强大。
(2)beta分布和 狄利克雷分布
(3) Latent Dirichlet allocation
M 步骤:
以及 alpha的表示方法
反复迭代从而让模型收敛。
(4) gibbs 抽样求解 lda
首先,假设一个作家写文章的过程是这样的,有一个 罐子 里边装有很多多面体,每一个多面体的n个面代表n个词, 作家每次 要写文章,都是选出来一些多面体,然后再转n面题去生成词。
所以一篇文章中的n 个词语可以表示为 一个多项式分布的形式:
多项式中的 概率组成的向量 p 服从狄利克雷分布:
根据狄利克雷 分布在 p向量 的积分为1 (p向量所有值累加为1),所以
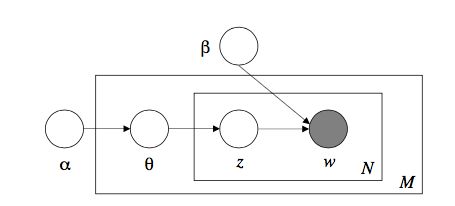
lda的概率图模型:
由 lda的概率图模型可以得出:
所以可以得到 :
(5) lda的多线程
我比较了解的lda多线程方法有两种:
第一种是 将语料库中的文章 分成 n 份,分开训练,每迭代一次 计算topic之间的相似度进行topic的合并。
这种方法我没有去实现,缺点我认为合并topic的过程会有误差发生,据说能提高 4倍左右。
第二种 方法是 将语料库中的文章分成n份,同步进行迭代训练, 将更新数组的地方加锁,同步更新。
这种方法进过验证之后,多线程的能比原来快4倍左右,缺点在于加锁之后,会有排队等待的时间,以 gibbs 并行通用的问题 收敛相比原始会稍微慢一些。
(6) label-lda
关于 label-lda 是之前我做过推荐算法方法遇到的一些问题,原始lda 是一个无监督聚类的过程,训练出来的topic 也是无意义的,如果用在推荐算法方面可能 推荐给用户的topic 本身有可能就是无意义的,会有一些差错在里边。
如果 我们的lda 可以像 新闻网站 给文章打下的标签一样自动打上标签,那么我们根据用户的兴趣直接给他们推荐他们喜欢的标签。
上图是一篇新闻稿 底部列出来的一些关键词,我们可以认为这是一篇文章的topic,label-lda的工作就是一篇文章没有这些关键词,可以用label-lda自动生成这些关键词(topic)。
具体过程是 , 在训练的过程中,首先初始化的随机分配过程 将文章中的所有词只分配到 文章自身带有的标签上, sample topic的过程 只比较 自身拥有的 标签,并给词选择标签中的其中的一个 作为 词的topic。
这样训练出来的topic 是一个标签指导的过程,每一个topic 就是标签训练的词的分布。
预测过程和原始lda 保持一致。
曾经用这种方法来进行分类,给两类语料分别打上 0 和 1 的标签,后来发现这个算法 训练 几百次和训练一次的结果是一致的,原因就是在于每个文章 只有一个标签,没有topic选择的过程。而这种方法就非常接近朴素贝叶斯的方法。
参考资料:
http://www.52nlp.cn/lda-math-%E6%B1%87%E6%80%BB-lda%E6%95%B0%E5%AD%A6%E5%85%AB%E5%8D%A6
http://yuedu.baidu.com/ebook/d0b441a8ccbff121dd36839a?fr=booklist###
Blei.Latent Dirichlet Allocation.2003.