poj 1698 Alice's Chance(基础网络流·建图)
题目:http://poj.org/problem?id=1698
Alice's Chance
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 6396 | Accepted: 2612 |
Description
Alice, a charming girl, have been dreaming of being a movie star for long. Her chances will come now, for several filmmaking companies invite her to play the chief role in their new films. Unfortunately, all these companies will start making the films at the same time, and the greedy Alice doesn't want to miss any of them!! You are asked to tell her whether she can act in all the films.
As for a film,
For example, assuming a film can be made only on Monday, Wednesday and Saturday; Alice should work for the film at least for 4 days; and it must be finished within 3 weeks. In this case she can work for the film on Monday of the first week, on Monday and Saturday of the second week, and on Monday of the third week.
Notice that on a single day Alice can work on at most ONE film.
As for a film,
- it will be made ONLY on some fixed days in a week, i.e., Alice can only work for the film on these days;
- Alice should work for it at least for specified number of days;
- the film MUST be finished before a prearranged deadline.
For example, assuming a film can be made only on Monday, Wednesday and Saturday; Alice should work for the film at least for 4 days; and it must be finished within 3 weeks. In this case she can work for the film on Monday of the first week, on Monday and Saturday of the second week, and on Monday of the third week.
Notice that on a single day Alice can work on at most ONE film.
Input
The first line of the input contains a single integer T (1 <= T <= 20), the number of test cases. Then T cases follow. Each test case begins with a single line containing an integer N (1 <= N <= 20), the number of films. Each of the following n lines is in the form of "F1 F2 F3 F4 F5 F6 F7 D W". Fi (1 <= i <= 7) is 1 or 0, representing whether the film can be made on the i-th day in a week (a week starts on Sunday): 1 means that the film can be made on this day, while 0 means the opposite. Both D (1 <= D <= 50) and W (1 <= W <= 50) are integers, and Alice should go to the film for D days and the film must be finished in W weeks.
Output
For each test case print a single line, 'Yes' if Alice can attend all the films, otherwise 'No'.
Sample Input
2 2 0 1 0 1 0 1 0 9 3 0 1 1 1 0 0 0 6 4 2 0 1 0 1 0 1 0 9 4 0 1 1 1 0 0 0 6 2
Sample Output
Yes No
Hint
A proper schedule for the first test case: date Sun Mon Tue Wed Thu Fri Sat week1 film1 film2 film1 film1 week2 film1 film2 film1 film1 week3 film1 film2 film1 film1 week4 film2 film2 film2
Source
POJ Monthly--2004.07.18
分析:大意:Alice要拍电影,有n部电影,规定Alice每部电影在每个礼拜只有固定的几天可以拍电影,每部电影可以拍w个礼拜,并且这部电影要拍d天,问Alice能不能拍完所有的电影。难点在于网络流系统的建图。大致的图案:
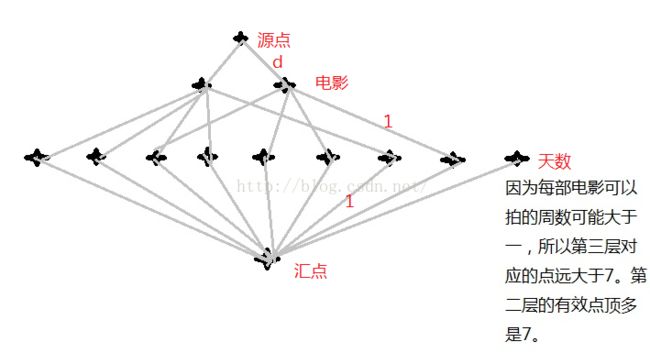
我发现数据大了后EK网络流算法不好用啊,要么是RE要么是MLE。。换个Dinic。
#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
const int N=400,INF=0x3f3f3f3f;
struct Dinic {
int c[N][N], n, s, t, l[N], e[N];
int flow(int maxf = INF) {
int left = maxf;
while (build()) left -= push(s, left);
return maxf - left;
}
int push(int x, int f) {
if (x == t) return f;
int &y = e[x], sum = f;
for (; y<n; y++)
if (c[x][y] > 0 && l[x]+1==l[y]) {
int cnt = push(y, min(sum, c[x][y]));
c[x][y] -= cnt;
c[y][x] += cnt;
sum -= cnt;
if (!sum) return f;
}
return f-sum;
}
bool build() {
int m = 0;
memset(l, -1, sizeof(l));
l[e[m++]=s] = 0;
for (int i=0; i<m; i++) for (int y=0; y<n; y++)
if (c[e[i]][y] > 0 && l[y]<0) l[e[m++]=y] = l[e[i]] + 1;
memset(e, 0, sizeof(e));
return l[t] >= 0;
}
} net;
int main()
{
//freopen("cin.txt","r",stdin);
int t,n,f[8],d,w;
cin>>t;
while(t--){
//memset(map,0,sizeof(map));
memset(net.c,0,sizeof(net.c));
scanf("%d",&n);
int i,j,k,wmax=0,dsum=0;
for(i=1;i<=n;i++){
for(j=1;j<=7;j++) scanf("%d",&f[j]);
scanf("%d%d",&d,&w);
net.c[0][i]=d;
dsum+=d;
wmax=max(wmax,w);
for(j=0;j<w;j++){
for(k=1;k<=7;k++){ // 汇点加上一周的7天是8
if(f[k]){ net.c[i][8+j*7+k]=1; }//map[i][n+j*7+k]=1; }
}
}
}
int final=7*wmax+7+1;
for(i=8;i<final;i++){
net.c[i][final]=1;
//map[7*i+n+j][final]=1;
}
net.t=final; //汇点
net.n=final+1; //点的个数,源点是0
int res=net.flow();
if(res==dsum) puts("Yes");
else puts("No");
}
return 0;
}