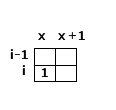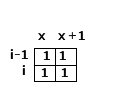poj 2411 Mondriaan's Dream (状态压缩dp 入门)
转载自http://blog.csdn.net/hopeztm/article/details/7841917
这个题目类属于状态压缩DP,对于状态压缩DP,其实最简单的理解就是把状态用比特位的形式表示出来,我们会在下面用例子来说明。
假如现在我们在铺砖 位置(i, j), 并且假设之前的位置已经铺设好的了,在这个位置,我们的选择:
1. 不用铺砖了,可能在(i-1, j)的时刻已经被竖着铺上了,然后考虑的是(i, j+1)
2. 横铺砖,将(i, j+1)也铺上了,然后考虑的是(i, j+2)
3. 竖着铺砖,(将i,j)和(i+1,j)铺上一个竖立的转头。
所以我们如下翻译我们的选择,在位置(i, j) 如果我们选择横着贴砖,那么将(i, j), (i, j+1)都填写成1, 如果竖着贴砖,我们将(i,j)填写成0, 将(i+1, j)填写成1.
为什么要这么计数呢,我觉得应该这样理解:
1. 在横着贴砖的时候,(i, j), (i, j+1) 都是1,这个值其实对下一行如何选择没有影响。
2. 竖着贴砖的第二个,我们也选择了1, 因为这个砖头结束了,对下一行如何选择依然没有影响。
3. 而竖着的第一个砖头,这个砖头是对下面有影响的,如果(i,j)是0,那么(i+1, j)只有是1的情况下才能满足条件。
(这涉及到接下来的 状态兼容性问题)
对于竖着贴砖为什么这样选择,这样选择的一个好处是,我们在处理最后一行的时候,可以保证最后一行都是1, 因为最后一行绝对不能成为 竖砖开始,所以很容易取得最后的解。
好了,我们把这样理解的方案画成图:
如果我们将每一行都理解成一个二进制数字,那么
Row1 = 51, Row2 = 15, Row3 = 48, Row4 = 63, Row5 = 51, Row6 = 63.
最后转头铺满的状态,一定是最后一行全是1。
我们用DP(i,j) 表示如下含义: 当第i行,达到状态j的时候,所能采取的方案数目。 所以明显我们的最后目的是求 DP(N, 2^(M-1)-1);
我们再来简单的分析一下为什么问题可以满足动态规划, 加入现在分析的对象是 DP(i,j), 那么这一行有多少种铺设办法是和上一行相关的,
如果上一行的某个状态DP(i-1,k) 可以达到 DP(i, j) 我们认为这两个状态是兼容的,如果DP(i-1,k)和DP(i, j)兼容并且 DP(i-1, k)有S中铺设方案,那么DP(i, j)就可以从DP(i-1, k)
这条路径中获得S个方案。 当然这里k的取值可以是 0 ~~~~ 2^(M-1) -1种取值。
现在我们来理解一下,什么叫做 j, k 兼容。
其实我们在上面已经基本给出分析, 如果我们现在铺设 (i,x) x这里表示第i行,第x列
1. 如果值 i 行,j 在x位上的值是0, 那么第 i-1行,j的值在x位上一定是1。因为不可能在同一列相邻的位置铺两个竖着的 第一个,如果满足下一步测试的是(i, x+1), 否则直接返回不兼容。
2. 如果值 i 行,j在x位置的值是1 .
{
那么有可能有两种情况:
1. (i-1, x)是0, 这个时候一定是竖着铺设了,下一步检测的是(i, x + 1)
2. (i-1, x) 是1, 如果是这样的话,那么(i, x)一定是要选择横着铺了,那么(i,x+1)也一定是1,并且(i-1, x + 1)一定是1(如果是0,就是竖着铺了),如果不满足就返回不兼容,满足条件 就测试(i, x + 2)
}
对于第一行的兼容性,我们要做一下特别的分析,在第一行中,要么放0, 要么放1。
加入当前测试的是 DP(0, j)的第 x的比特位,即第0行,x列
1. 如果x是1,那么 x + 1 也一定是1,然后测试到 x + 2
2. 如果x是0, 那么直接测试下一个 x + 1
补充说明一点,当测试循环中,我们有时候必须要移动 1 位,有时候移动2位,当需要移动2位并且 x == M - 1(M列数)的时候,说明已经不可能兼容了。
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int N = 12;
long long dp[N][15000];
int high,width,m;
bool TestOne(int date)
{
int i = 0;
while(i < width)
{
if(date & (1 << i)) //第i列为1
{
if(i == width - 1 || (date & 1 << (i+1)) == 0) //如果最后一列为1或者第i+1位为0,则不成立
{
return false;
}
i += 2;
}
else
{
i++;
}
}
return true;
}
bool Test(int date1,int date2) //date1 表示第 i 行,date2 表示第 i-1 行
{
int i = 0;
while(i < width)
{
if((date1 & (1 << i)) == 0)
{
if((date2 & (1 << i)) == 0)
{
return false;
}
i++;
}
else
{
if((date2 & (1 << i)) == 0)
{
i++;
}
else if(i == width - 1 || !((date1 & (1 << (i+1)))&&(date2 & (1 << (i+1)))))
{
return false;
}
else
{
i += 2;
}
}
}
return true;
}
int main()
{
//freopen("Input.txt","r",stdin);
int i,j;
int k;
while(~scanf("%d%d",&high,&width),high + width)
{
if(high < width)
{
swap(high,width);
}
//printf("%d %d\n",width,high);
int m = (1 << width) - 1;
//printf("%d\n",m);
memset(dp,0,sizeof(dp));
for(j = 0; j <= m; j++)
{
if(TestOne(j))
{
dp[0][j] = 1;
}
}
for(i = 1; i < high; i++)
for(j = 0; j <= m; j++)
for(k = 0; k <= m; k++)
{
if(Test(j,k))
{
dp[i][j] += dp[i-1][k];
}
}
printf("%lld\n",dp[high-1][m]);
}
return 0;
}