林达华08到10年的博客

作者：金良（[email protected]） csdn博客：http://blog.csdn.net/u012176591

DDP的背后

这次在NIPS 2010上发表的关于构造Dependent Dirichlet Processes (DDP)的paper在NIPS的官网已经可以下载了。

在这里只是想分享这篇文章背后的研究经历。

认识我的朋友们应该知道，我从本科开始直到现在，主要研究方向一直都是computer vision。但是，在硕士阶段和在博士阶段的研究目标却有着很大的不同，这和导师的风格有着很重要的关系。

在香港读硕士期间，我的导师汤老师是一个非常注重实际应用的人，因此当时做research的主要目标是提高实际性能或者建立新的应用。在方法上，更多地是借用现有的方法，或者略加改进。

到了MIT之后，我的导师Eric Grimson让我在John Fisher的指导下进行研究。John和LIDS的主任AlanWillsky关系很密切，因此我每周都要参加Alan的一个grouplet，并且有幸和Alan讨论学术问题。

Alan Willsky是我非常敬佩的一位教授，他有着很深的数学造诣。在每次grouplet的时候，他都听我们给他讲新的进展，而他则为下一步的研究提供方向性的意见。和汤老师的风格不一样，Alan是一位很典型的理论型的科学家。每次讨论时，他关注的重点不是实验结果，而是理论价值，比如某一个方法是不是能给这个field带来新的insight。在他前几年指导的工作里面，这一点得到了充分的体现，比如Tree reweighted approximation和Walk-sumanalysis of Gaussian LBP都是probabilistic inference的重要进展，并且展现了对相关领域的深入而独到的理解。

在他的引导下，我在研究过程中更多地思考一个工作背后的理论基础。在这个过程中，我始终感到在本科和HK时期打下的数学基础并不足以支持在理论方面的深入探索，于是开始系统地学习和我的研究课题有关的数学。和运动分析有关的部分主要是Differential geometry和Lie algebra，和统计模型有关的是Measure theory，Modern probability theory，Stochastic processes和Convex analysis。以及这些学科所共同涉及的General topology和Functional analysis。

MIT要求每个PhD修一门minor，我当时从我的需要出发选择了数学(Course 18)。在这个过程中得到了进行严格数学推导和证明的训练。进行严格的数学分析和推演的能力也许在Computer Vision的大部分工作中并不是特别需要，但是在做NIPS这个工作的时候它的效用就显现出来了。理论上的东西，你要说服别人它是对的，必须给出严格的证明，而不仅仅是实验结果。

回到这篇NIPS paper吧。最初，我们是希望得到一种能随着时间变化的mixture model。在这个过程中，可能回增减其中的component。如果回到硕士的时代，也许，我们会通过工程的方法来解决这个问题——事实上很多现有的工作就是通过工程方法或者算法层面的设计来达到这个目标的。但是，基于我们组的风格，我们并不能满足这样的方法，而是希望每个方法都有一套严格的数学理论去支持。

在mixture演化的过程中component的个数会发生变化，因此Dirichlet Process也就成了很自然的一种选择。一开始的时候，我们也只是希望对原有的基于Polya Urn或者Stick breaking的方法加以改进来满足我们的需求，但是发现这其中在数学上存在很多困难，于是，我们开始尝试另起炉灶，从根源重新理解DP。

在我早前做关于大批运动物体的motionanalysis的topic的时候，曾经读过一些关于RandomPoint processes的书，其中包括Kingman的Poissonprocesses。这本书中提到了(Spatial) Poisson process的很多很漂亮的数学性质，以及它和Gamma/Dirichlet Process的内在关系。最初读这本书的时候，只是惊叹于Poissonprocess的数学美，而并没有意识到它的实际价值。当我再次阅读这部书的时候，才形成了是否可以利用Poisson和Dirichlet的关系来建立我们的dynamic mixture modelframework的想法。这种想法就是这篇NIPS的源头，paper中的section 2关于数学background的部分就是来自于这本书。

在我早前的blog中曾经论及空间泊松过程和随机测度，其实已经是在一定程度上介绍这篇paper的理论背景。只是当时paper还没有发表，并不便于讲得很深入。

除了Alan的影响，我也感谢John和Eric为我创造的研究环境。一直以来，对于在理论方面的探索，他们都是非常鼓励的，认为这样的探索非常有价值。虽然，我们的funding也需要一些项目来支持，但是，John尽了很大的努力排除这些项目对于研究的干扰——他向sponsor提出一个要求是，我们可以为他们提供新的方法或者模型，但是sponsor不应干扰或者介入具体的研究课题以及课题的选择。

在这次NIPS的会议上，我看到了很多很好的很有启发的工作。跟许多参加会议的学者相比，我目前所做的这些工作（包括这篇paper）其实还是非常有限的。这次提出的方法本身也有着很多的局限有待解决，比如目前只是支持sequential filtering，而且Sampler的efficiency的提高还有很大的空间。让这次提出的方法在领域内产生真正的影响，还需要做很多的事情。

Postedby dahuasky  |  12月 10, 2010 

NIPS outstanding studentpaper award

I am glad to share a good newswith all my friends.

My paper with title“Construction of Dependent DirichletProcesses based on Poisson Processes” receives theoutstanding student paper award in NIPS 2010.

Relevant information can be foundin the NIPS program booklet. Two papers out of 1200+ are awarded and two othersgot honorable mentions.

My gratitude is delivered to Prof.Grimson, Fisher, and Willsky, as well as all the friends who have beensupporting and encouraging me along my academic exploration.

The basic idea of this work is toexploit the theoretical connections between Poisson, Gamma, and Dirichletprocesses in constructing dependent Dirichlet processes. The constructionproposed in this paper has essential differences from the traditionalconstructions that are based on either Polya urn (Chinese restaurant process)or stick breaking. I believe that this work is only a starting point along theline in exploiting this relation, and there remains a lot of room for futureexploration. I would be really happy if there could be lots of efforts along thisdirection that make it into an important methodology in Nonparametric Bayesianlearning and estimation. Had this happened, it could be much more significantthan this paper itself.

The paper is available by thefollowing link:

https://dahuasky.files.wordpress.com/2010/12/ddp_nips10.pdf

Here is the supplemental document,which contains the description of relevant math concepts as well as the proofsof the theorems in paper:

https://dahuasky.files.wordpress.com/2010/12/supplement_doc.pdf

Any feedback is highlyappreciated. Thank you.

Postedby dahuasky  |  12月 2, 2010

Blog搬家了

为 Live Space 默哀。。。。。。这个新家还真不习惯:-(

Postedby dahuasky  |  09月 29, 2010

Learning和Vision中的小进展和大进展

首先祝朋友们中秋节快乐！

因为过去三个月的实习工作很繁忙，这么已经很长时间没有更新了。这个夏天参加了两次会议(CVPR和ECCV)，在微软完成了一个新的project，这些经历都给了我新的启发。
不积跬步无以至千里
很多在这个领域做research的朋友抱怨，这个领域在过去相当长的时间没有“突破性”的进展了。在过去，我也一直抱有这样的看法。不过，如果比较最近两年的paper，以及20年前的paper，其实，还是可以看到，在很多具体的方向上，我们都已经取得了长足的进展。很多在当年只是处于雏型阶段的算法和模型，经过整个community这么多年的努力，现在的性能已经接近或者到达实用的水平。

虽然，在每年的各大会议中，非常激动人心的paper很少，可是，如果我们把某个方向过去10年的文章串在一起，我们会发现，这个方向的前沿已经推进了不少。这个过程有点类似于进化。在每年发表的成百上千的paper中，真正有价值的贡献只占很小的比例。但是这小部分的贡献能经历时间的考验，被积淀下来，并且被逐步被广泛地接受。当这样的进展积累到一定程度，整个方向就已是今非昔比。

在这个过程中，不同类型的paper其实发挥着不同的作用。举一个简单的例子，在很多问题的传统模型中，因为建模和计算的方便，都喜欢使用L2 norm来测量与观察数据的匹配程度。而近年来，越来越多的模型开始改用L1 norm来取代L2 norm，并且在性能上获得很大的提高。这样的变化起码经历了10年时间才逐步受到广泛的注意。在较为早期的工作里，部分的researcher在实践中发现似乎用L1 norm性能更好，但是大家并不是一开始就深入了解这背后的原理的。于是，这样的观察也许只散见于不同paper的experiment section或者implementation details里面。随着这种观察被反复验证，就会有人进行系统性的实验比较，使得这些观察形成更为可靠的结论。另一方面，理论分析也随之展开，希望能从更深的层次上来剖析其背后的原理，甚至建立严格的数学模型——于是一个本来只是实验中的heuristic的方法终于具有了稳固的理论根基。这些理论将启发人们提出新的方法和模型。

也许在很多人看来，从L2 norm到L1 norm的变化，只是一字之差，不值一提。但是，这种变化对于全领域的影响非常深远，不仅仅在很多具体的topic上带来性能提高，而且引导了学科的发展趋势——robust fitting,sparse coding / compressed sensing受到热情关注，和这种变化是密切相关的。

我在和一些同学交流的时候，发现有些人特别热衷于解决“根本问题”。壮志固然可嘉，但是，我始终认为，根本问题的解决离不开在具体问题上的积累和深刻理解。这种积累，既包括理论的，也包括实验的。至少，对于像我这样的普通人，我觉得，获得这种积累的唯一途径就是大量的实践，包括阅读paper，建立数学模型，推导求解算法，自己亲手把程序写出来，在实际数据中运行并观察结果。新的idea是思考出来的，但是，这种思考是需要建立在对问题的深刻理解上的。从石头缝里蹦出有价值的idea的概率，和彩票中奖没有什么区别。

什么是有价值的？

每个人对于一个工作的价值会有不同的判断。我在这里只是想说说我个人的看法。Research和 Engineer 不太一样的地方在于，后者强调work，而且倾向于使用已经proven的方法；而前者更强调novelty——创新是Research的生命。

一直以来，一些paper有这样的倾向，为了显示这个工作的“技术含量”，会在上面列出大段的数学推导，或者复杂的模型图。很多的推导只是把一些众所周知的线性代数结论重新推一遍，或者重新推一下kernel trick，又或者optimization里面的primal dual的变换。可是这些东西再多，在有经验的reviewer看来，只是在做标准作业，对于novelty加分为零。

真正的创新，在于你提出了别人没有提出过的东西。创新的内涵可以是多方面的：

• 建立了新的数学模型，或者提出了新的解法
• 提出的新的应用
• 提出新的框架，用新的方式来整合原有的方法
• 在比较性实验中获得新的观察
• 统一本来分开的领域，模型，或者方法

创新可以体现在从理论，建模，求解和实验的各个环节之中。判断创新与否的关键不在于有多高深的数学，不在于使用了多时髦的方法，不在于做一个多热门的topic，而在于是否make a difference。

另外，我觉得，创新的大小不能绝对而论。有一些在实验中用于improveperformance的小trick，也许能被有理论基础的researcher开拓成全新的方法论，甚至建立严密的数学基础。很多paper中都埋藏着这样的金子，等待trained eyes的发掘（可能连paper的作者自己都没有意识到~~）

Postedby dahuasky  |  09月 23, 2010

离开加州

在Microsoft Research Silicon Valley的intern结束了。感谢Simon，帮助我创造了一段愉快的工作经历。也要感谢Chen Wei，让这个本来枯燥的暑假增色不少。

 

在今天傍晚，将直接从San Francisco飞往希腊——开始一次让人憧憬的旅程。再见了，加州。

 

 

 

 

Postedby dahuasky  |  09月 3, 2010

From NIPS 2010

We are pleased to inform you that your NIPS2010 submission "Construction of Dependent Dirichlet Processes based onCompound Poisson Processes," paper ID 71, has been accepted forpublication in the conference proceedings, with a full oral presentation at theconference. 

There were a record 1219submissions to NIPS this year, with many strong submissions. The programcommittee selected 293 papers for presentation at the conference; among these,only 20 papers were selected for full oral presentation, of which yours is one.Congratulations!

－－－－－－－－－－

过几天就要离开阳光加州（真是很阳光，三个月居然不见一滴雨～～～），启程参加ECCV了，希望在希腊有一个愉快的旅程，认识新的朋友。

Postedby dahuasky  |  08月 29, 2010

本年度CVPR最有趣的文章

在今年的CVPR，见到了很多朋友，也看到很多Paper。

在这次会议里面让我最喜欢的一篇Paper，却不是在会议中正式发表的，而是在TC Panel派发的。这篇Paper的题目叫Paper Gestalt。文章以诙谐的笔调描述了一个基于vision +learning的自动paper review算法。

参加会议的朋友们可以很幸运的在会场获取这篇文章，至于没有来的朋友，我想只能向作者（这位兄弟（也许是姐妹）在paper中自称Carven von Bearnensquash,[email protected]）索要了。

这篇论文出炉的背景，就是最近几年CVPR或者ICCV的submission呈现急速的指数增长的趋势（在过去10年翻了三倍）。按照这个速度增长，在 10年后每次会议的投稿量就会超过5000篇！也许最好的办法是采用“货币杠杆”进行“宏观调控”——就是对投稿者收费。比如，对每个 submission征收100美元的费用，我相信对于投稿的数量和质量都会取得立竿见影的效果。一方面，很多纯粹是来碰运气的作者会掂量一下花100块 钱来博取1%的命中机会是不是值得；而持认真态度的作者则会对paper精益求精，免得投稿费白白浪费；而最终文章被录用的作者就可以减免注册费，会议方 面也有更多的funding来给有志于为Computer Vision奋斗的学术青年发放参加会议的路费。一举四得，何乐不为，呵呵。

当然了，涉及到钱的问题，自然要经历很多微妙的利益博弈——这些事情还是让Chair们去担心好了。这里，我们还是继续“奇文共欣赏”吧。文章的算法很简 单（前提是你对Machine Learning或者Computer Vision有一点了解），把8页的pdf文档并排成一张长的image，然后就在上面抽feature。做自然语言处理的朋友们请不要激动，这是 Vision的paper，自然用的是Vision圈子自己的方法。好了，抽什么feature呢？主要是HOG(Histogram of Gradients)，这是一种纯粹用于描述视觉观感的feature。显然，大段的文本，曲线图，图像，表格，数学公式，它们的feature应该是不太一样的。然后作者用AdaBoost做feature selection训练得到一个分类器：纯粹根据paper的视觉观感来判断paper的好坏。

说到训练分类器，自然需要一个训练集。这篇文章的作者收集了CVPR2008, ICCV 2009和CVPR 2009的全部1196篇paper构成正样本。那么负样本从何而来呢？被拒的paper显然作者是拿不到的。于是他很聪明的利用了一个众所周知但是大家却不会公开明言的事实：workshop接纳的很多是在主要会议被拒收的paper。这样，很不幸的，workshop上发表的文章被用作负样本。在 Workshop上发表了论文的同志们不要打我——我只是讲述一篇别人的文章，这个主意不是我出的。

最有趣的部分要数实验结果了。从ROC曲线来看，结果其实还是不错的——以拒绝15%的正样本为代价，可以滤除一半的负样本。作者对于正负样本的特征做了 一些总结，也许对于大家以后投paper还是有点指导意义呢。。。

正样本的“视觉”特点：
1. 里面有几段公式，看上去文章显得似乎很专业，也显得作者似乎数学不错；
2. 实验部分里面多少要有几个曲线图，即使那几个曲线图说明不了什么。但是，只要有几个曲线图在那里，起码表示我做的是“科学实验”；
3. 最好在文章开头或者最后一页排列一堆图像。其实，我也注意到很多作者喜欢排列很多dataset里面的图像到paper上——即使那是一个 publically available的standard dataset——我不知道这样做的意义何在——除了审美效果。
4. 最好写满8页，代表分量足够。

负样本的特点：
1. 不够页数。在submission阶段，写不满6页的文章被录用的机会很小。虽然最后很多本来8页的文章还是能很神奇地被压缩到6页，如果作者想省掉 200美元的附加页费。题外话，我也一直不明白为什么多一页要多交100美元注册费。
2. 有很大的数字表，就是m行n列，排满数字那种。这篇文章表明，排列了很多曲线图和柱状图的文章比排列了很多数字表的文章有更大概率被接收。
3. 没有漂亮插图。

这篇文章的结果，我也做一些补充评论。
1. CVPR和ICCV的录用结果，对于文章的视觉观感，有着显著的统计相关。从我自己做Reviewer的经验，以及和其它reviewer的交谈来说，这 个确实在一定程度上影响了reviewer的第一印象，甚至是评价基调。一篇文章在first glance给人以专业和有内涵的感觉，会有利于它在reviewer心中树立良好印象。这与学术无关，但是，很不幸，却是一个普遍存在的事实。

对于NIPS这种理论取向的会议，虽然不需要那么多漂亮的图表，但是，文章要“长得”像这些会议的文章。让人觉得写文章的是一个有经验的研究者，而不是一个打酱油的。

2. Workshop的文章和CVPR/ICCV主会似乎存在明显差距，以至于一个如此简单的分类器都能够在区分它们的任务中取得不俗的成绩。另外，作者使用 workshop paper作为负样本的做法虽然是个人选择，但是，起码在一定程度上反映了这个community对于workshop的态度。

3. 近年来CV paper的投稿量的高速增长，已经严重影响了review的质量。一方面，会议不得不邀请许多没有很多经验的学生参与到review的过程，即使文章是 发到senior researcher的手中，最终还是会被传递到他的某个刚入行的学生那里作为学习reviewing的“牺牲品”。我甚至听说过有reviewer为了 应付due date，把文章交给秘书或者亲戚来审，其结果可想而知了。另外，reviewer也没有足够的时间来仔细的审读paper。很多情况下，读完 abstract和intro，大概翻翻实验结果以及文章的插图，已经基本形成对文章的定性。如果reviewer喜欢这篇paper，它会根据作者的 claim对文章表示赞赏；如果不喜欢这篇文章，就会找一些似是而非的理由把文章拒掉。

当然了，最后我们还有rebuttal，然后由AC meeting来确定文章的生死。Area Chair大多是成名学者，个人的学术水平还是由一定保证的。但是，他们非常繁忙，AC meeting虽然目的是给每篇文章一个decision，但是在一些AC的心目里，这主要是一个旅游和social的机会。大部分的final decision就是根据review结果照本宣科（一个不成文的规矩是review rating的中位数是2作为录取划线标准）。另外，AC大概会看看abstract和rebuttal，然后酌情裁量。

Postedby dahuasky  |  06月 18, 2010 

« Older Entries

CVPR 2010 Kick off

CVPR 2010 即将开始了。

 

注册参加会议的人数已经创纪录地突破1800了！Really crazy。。。。我看到好多几年不见的朋友都来开会了，一定很热闹~~这回咱也算是半个东道主了。

 

 

Postedby dahuasky  |  06月 13, 2010

开始在加州的阳光生活

昨天晚上刚到了Mountain View，开始了在加州三个月的internship。这是我第三次回到Microsoft Research，不过这次又换了一个地方——微软硅谷研究院。（把这次算上，微软在全球的六个研究院，已经去过其中一半了～～～）

再见了，Boston的朋友们，我会挂念你们的。。。。。。

Postedby dahuasky  |  06月 7, 2010

Notes on Martingales, RandomWalks, and Brownian Motion

 

快到期末了，整理了一下18.445后半段的一些笔记，形成了一份notes。

 

http://people.csail.mit.edu/dhlin/stoc/mrb.pdf

 

这部分的课程主要是关于Martingale（鞅），Random Walk（随机游走），还有Brownian Motion（布朗运动）的基本内容。

重点是在使用Martingale, Optional StoppingTheorem, Reflection Principle, 还有Wald’s Identity，对Random Walk和Brownian Motion进行分析。

希望这份notes对于希望学习或者复习有关内容的朋友有帮助。

 

18.445其实只是MIT数学系对于随机过程理论的入门要求，不过在还是要求对测度理论和现代概率理论的基础有比较扎实的掌握的。

起码应该熟悉Sigma代数的独立性，基于Sigma代数定义的条件期望，以及关于可测函数（随机变量）的不同方式的收敛。

 

Postedby dahuasky  |  05月 4, 2010 

Book List Updated

这个Blog上的数学书单已经有很长时间没有更新了。今天抽了一点时间，update了一下。现在分成三个列表，分别是

 

Algebra, Analysis, and Geometry

 

代数，分析，和几何是现代数学的三大基础分支。在这些科目上的扎实基础对于理论探索是非常重要的。而点集拓扑则是分析和几何的共同基础。而抽象代数则是相对独立的一个分支，但是抽象代数中的很多概念和思想则广泛渗透于其它数学学科之中。

 

而在分析中，实分析是一切分析的基础。在此基础上，发展出来的复分析，泛函分析，调和分析，和微分方程理论，在工程实践中都有重要应用。对于机器学习领域来说，泛函分析的希尔伯特空间理论和算子谱论发挥着核心作用（比如Reproducing Kernel Hilbert Space, Markov Process的转移核的谱）。调和分析则在信号处理和分解方面起着关键作用（傅里叶变换就是调和分析的研究内容之一，另外，现在非常火热的compressed sensing或者sparse coding的数学根源也是调和分析）。

 

微分方程理论，以及李群和李代数理论则是对动态过程进行建模的重要工具。而很多随机过程也和它们有密切关系，比如Markov Process的抽象分析往往可以归结为Markov Semigroup，这是一种类似李群的连续半群系统。而连续时间Markov process的分布变化则可以通过微分方程(比如Komolgorov Equation或者Fokker–Planck Equation)描述。

 

Optimization and Numerical Computation

 

这个列表主要以优化方面的书为主。目前常用的优化包括一般的数值优化（比如GradientDescent），凸优化(Convex Optimization)，组合优化(Combinatorial Optimization)，还有线性优化(LinearProgramming)。其中，线性优化虽然可以视为凸优化的一个特例，但是它太特殊了，因此需要单列出来，而且它和组合优化有着千丝万缕的联系（比如很多基于图和网络的优化问题）。

 

Probability Theory and Stochastic Processes

 

这个列表主要包括两个方面的书：现代概率理论 和 随机过程。

 

现代概率理论的基础是测度理论。对测度理论和在此基础上建立的积分理论的切实理解是学好现代概率论的重要基础。在现代概率论的许多重要概念中，比如independence, conditional expectation, martingale，可测性都起着核心作用。

 

而随机过程考察的是随机函数，虽然很多时候它们是定义在时间上的，不过很多过程可以拓展到空间上——比如高斯过程和泊松过程。在众多的随机过程概念中，我觉得有一些是特别需要深入理解的：Markov, Brownian motion, Gaussian Process, Martingale，还有Poisson Process。

 

作为Gaussian Process的重要特例，Brownian motion在研究连续时间过程中扮演特别重要的角色。Diffusion，还有随机积分和随机微分方程理论就是在其基础上建立。

 

列在单上的书都是我在学习过程中觉得写得比较好的。其中，只有不到一半是整本看完的，另外一些则是看了部分章节。希望对大家有帮助。

 

 

 

 

Postedby dahuasky  |  04月 23, 2010 

空间点过程与随机测度（二）：测度的故事

既然这个Topic的题目是关于随机测度，那么，自然是离不开“测度”(measure)这个概念的。所以在这篇文章里，我们要说一说测度。也许，在很多朋友的眼中，“测度”是一个特别理论的概念——似乎只有研究数学的人才应该关心它。这也许和大学的课程设计有关系，因为这个概念一般是在研究生的数学课程才会开始讲授，比如“实分析”或者“现代概率理论”。而且，在大多数教科书里面，它的第一次出场就已经带着厚厚的面纱——在我看过的大部分教材里面，它总是定义在sigma代数之上，而sigma代数听上去似乎是一个很玄乎的名词。

测度，其实很简单

在这里，我只是想拨开测度的神秘面纱——其实，测度是一个非常简单的事情：理解它，只需要小学生的知识，而不是研究生。

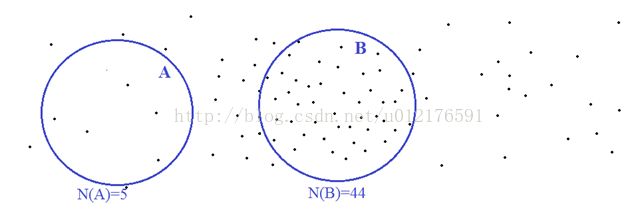
还是回到我们数星星的例子。

在这个例子里面，我们定义了一“数星星”函数，用符号N表示。这个函数的输入是一个集合（比如A和B），输出是一个数字——该集合中所包含的“星星”的数目。我们看看，这个函数有什么特点。首先，它是非负的，也就是说不可能在一个区域中含有“负数”个星星。其次，它有“可加性”。这是什么意思呢？

比如说，在上面两个不相交的区域A和B里面，各自包含了5个和44个点。那么在A和B的并集总共包含了49个点。换言之，N(A U B) = N(A) + N(B)。

严格一点的说，如果一个“集合函数”，或者说一个从集合到非负实数的映射，如果它在有限个不相交集合的并集上取的值，等于它在这些集合上分别取的值的和，那么我们就认为这个函数具有“可加性”。更进一步的，如果它在可数无限个不相交集合的并集上符合这样的可加性，那么我们就说，它是“可数可加”(Countably additive)。

一个非负“集合函数”，如果对空集取值为0，并且在“一系列集合上”具有可列可加性，那么这个“集合函数”就叫做一个“测度”(Measure)。作为例子，上面的“数星星”函数就是定义在所有二维空间子集上的一个测度。同样的，我们可以举出，很多具体的“测度”的例子，比如：

1. 各个区域内的所有星星的总质量
2. 各个区域的面积大小

不可测集和分球悖论

不过，在某些条件下，测度并不能定义在全部子集上。说通俗点，就是对其中一些集合，我们不可能定义出它的测度。比如说，在二维平面，我们可以按照一般的理解定义面积函数，比如长和宽分别为a和b的长方形面积为ab。对于复杂一点的形状，我们可以通过积分来计算面积。但是，是不是所有的二维平面的子集都存在一个“面积”呢？正确的答案显得有点“违背常识”：在承认选择公理(Axiom of Choice)正确的情况下，确实有一些集合没法定义出面积。或者说，无论我们在这些集合上定义面积为多少，都会导致自相矛盾的结果。

这里要注意的是，“没法定义面积”和“面积为零”是两回事。比如，在二维集合上的单个离散点或者直线，面积都是零。而那些“没法定义面积”的子集——我们称之为“不可测集”都是一些非常非常奇怪的集合——对于这些集合，我们把它的面积定义为零，或者别的什么非零的数，都会导致自相矛盾。这样的集合是数学家们用特殊的巧妙方法构造出来的——在实际生活中大家是肯定不会碰到的。这样的构造并不困难，但是很巧妙。有兴趣的朋友可以在几乎每本讲测度论的教科书中找到这种构造，这里就不详细说了。

（注：上图不是我制作的，而是出自http://www.daviddarling.info/）

关于不可测 集，有一个很著名的“悖论”，叫做“巴拿赫-塔斯基分球悖论”(Banach-Tarski Paradox)。如果说，某些奇怪的集合不能定义出面积还能让很多人勉强接受的话，那么“塔斯基分球”可能会让很多人“简直无法接受”——包括在上世纪二三十年代的很多著名数学家。这个“怪论”是这么说的：

我们可以把一个三维的半径为1的实心球用某种巧妙方法分成五等分——五等分的意思是，把其中一份旋转平移后可以和另外一份重合——然后把这五个分块旋转平移后，可以组合成两个半径为1的实心球。简单的说，一个球分割重组后变成了两个同样大小的球！

当然了，这样的过程还可以继续下去，两个变四个，四个变八个。。。。。。有人说，这显然不正确吧，然后他这么Argue：

如果一个实心球体积为V（因为球的半径是1，所以V > 0），那么五个等分块，每块体积为V/5，平移旋转不改变体积，所以，无论它们如何组合，最后得到的东西总体积是V，而不可能是2V。

但是，这样的说法在传统意义下确实没错——你拿去中学老师那里，肯定会被称赞是一个善于思考的好孩子。但是，我在更广义的条件下考察，就有问题了。因为，这个论述是基于这么一个假设：每一个分块都是有“体积”的。而塔斯基分球的精妙之处就在于它把球分成了五个“不可测集”——也就是五个“无法定义体积”的奇怪分块。所以，这里我们说“五等分”只是说它们其中一块平移旋转后能重合到另一块上，并不是说它们“体积相等”——因为根本就没有体积，也就没有相等之说。

这个分球术可以通过抽象代数里面对于自由群的分解来实现。对于塔斯基分球有兴趣的朋友，可以参考Leonard M. Wapner的数学读本The Pea and the sun: amathematical paradox。

细心的朋友可能注意到了，不可测集的构造也好，塔斯基分球也好，都是基于对“选择公理”(Axiom of Choice)的承认。如果我们不承认它，不就没事了么？在我们拒绝承认“选择公理”之前，我们首先要知道“选择公理”究竟是什么东西。通俗一点的说，选择公理可以这么描述：

任意一组（可能有不可数无限个）非空集合，我们都可以从每个集合挑出一个元素。

看上去非常“无辜”啊——这不就是典型的“正确的废话”么——所以它被叫做“公理”。可是就是这么一个公理，却是魔力惊人，能让我们把实心球一个变俩。这就是数学的魅力！

在历史上，巴拿赫和塔斯基提出分球悖论的年代，正是数学家们对选择公理的存废进行激烈争论的年代。数学家们分成两派，一派支持“选择公理”，另外一派则反对它。而巴拿赫和塔斯基这两位数学天才在当时原是反对接受选择公理，所以它们煞费苦心找到这个分球方法，目的就是以这种令人难以接受的“荒谬现象”来否定选择公理。而在后来的发展中，大部分数学家还是认识到选择公理对于现代数学发展的重要意义（比如，泛函分析中的核心定理——Hahn Banach延拓定理就依赖于对选择公理的承认），而选择接受它，当然塔斯基分球这种“怪现象”也被接受了。现在，“巴拿赫-塔斯基分球悖论”又被称为“巴拿赫-塔斯基分球定理”——从悖论变成定理了。

数学就是这样一个奇妙的世界。它往往基于我们的生活常识建立起来，但是一旦建立起来就要遵循它本身的发展规律，哪怕它有时候违反“常识”——人们能直观认知的常识是有限的，而数学的威力能把我们带到常识所不能触及的地方。

测度与集合的代数结构

测度和集合的运算是密切相关的。根据测度的定义，如果A和B是两个不相交的集合，如果A和B的测度被确定之后，它们的并集的测度也就确定了，就等于它们各自测度的和。如果B是A的子集，那么如果它们的测度测定，那么它们的差集A – B的测度也就确定了，等于A和B的测度的差。所以，当我们要定义一个测度的时候，其实往往不需要对所有的集合都作出定义，只要对一部分集合定义好了，其它集合的测度也就确定了。

我们说了不相交集合的并集，以及差集，那么对于一般的并集呢？如果A和B是两个可能相交的集合。那么它们的并集A U B可以分成三个不相交的部分：A – C, B – C，以及C三个部分，这里C是A和B的交集。只要知道交集C的测度，根据不相交并集和差集的测度公式，我们就可以知道A – C, B – C，以及A U B的测度。可是仅仅知道 A 和 B的测度，它们的交集的测度是显然不能确定的——两个即使是同样大小的集合，可能相交很多，甚至重合，也可能不相交。

所以，要有效定义一个测度，我们首先需要确定它在一系列集合以及它们的所有交集上的值。这样，这些集合的所有并集和差集的测度也就给定了。数学家把这种观察归纳成一种代数结构——集合上的Semiring——注意这和抽象代数里面的semiring不是一回事。S是一组集合，如果S中任意两个集合的交集仍在S内，S中任何两个集合的差集都可以表示为S中其它有限个不相交集合的并集，那么S就叫一个semiring。那么，只要对S中的集合定义好测度，那么由这些集合的可数次交集并集差集运算产生的那些集合的测度也就确定了。

一组集合，如果包含空集，并且对可数次交集并集补集运算是封闭的，那么这组集合其实就是一个Sigma代数。从某种意义上说，如果我们确定了一个覆盖全集的semiring上的测度，那么整个sigma代数中所有集合的测度都确定了。这可以和线性空间做一个不太严格的类比。在线性代数里面，对于一个线性函数，如果它在基上的函数值确定了，那么它在整个线性空间的函数值也就确定了。对于测度，semiring好比是“基”，而sigma代数则好比是整个空间。

数星星的数学还在继续：随机测度

回到数星星的过程。上面我们讨论过了，数星星其实就是一个测度。可是，每天晚上我们看到的星星分布都在变化的。也就是说，每数一次星星，就会得到一个不同的测度。这和掷骰子有点像。每掷一次骰子，我们的得到一个不同的点数——这个点数可以被看成是一个随机变量，变量的值是1到6的整数。同样的道理，星星的分布不确定，每数一次得到一个不同的测度——这也可以看成是一个“随机变量”，只是这里变量的值是一个测度，而不是一个数字。这样的一种以测度为值的“随机变量”，叫做“随机测度”(Random Measure)。这是在接下来的文章中要继续讲述的故事。

Postedby dahuasky  |  04月 21, 2010

空间点过程与随机测度（一）：从数星星说起

Blog的更新刚刚恢复，就得到大家的鼓励，真是让我感动，谢谢大家了。

数星星的数学

从今天开始，我打算分几篇来分享一个我认为是概率理论中一个非常漂亮的Topic：空间点过程(Point Processes)和随机测度(Random Measure)。

小时候，在晴朗的夜里，我喜欢仰望星空，去数天上的星星——那是无忧无虑的快乐童年。长大后，当我们再度仰望苍穹，也许会思考一个不一样的问题：这点点繁星的分布是不是遵循什么数学规律呢？这个问题也许问得太不解风情了。但是，在这篇文章里，我希望向大家表达的是，这个问题会把我们带入一个比星空更为美丽的数学的世界。

探讨这个问题，不需要什么高深的方法。还是和我们小时候一样，我们从“数星星”做起。相比于整个夜空，每个星星是在太小太小了，所以，我们可以做一个简化的设定：把每颗星星看成是一个点——一个没有大小的点——在我们的讨论中，我们只关心星星的位置和数目，不关心它的大小和形状，更不会关心那上面也许存在的外星人。（在之后的连载中，还会讨论这些星星的重量，以及它们在历史长河中的产生，运动，和消亡。）

我们开始数星星。为了方便，我们把整个星空分成不相交的区域，然后分区数数。在上面这个图里面，我画出了两个区域：A和 B。N(A)和N(B)分别表示，这两个区域里面的星星的个数。我们可以看到，星星的分布可能是不均匀的，有些地方稀疏一些，另外一些地方稠密一些。所以，虽然A和B的面积差不多，但是，里面包含的星星数目却相差好多倍。

由于各种各样的原因，我们每天看到的星空中星星的分布可能都在变化。即使同一个区域，里面包含的星星数目也可能是不确定的——这就是概率理论能发挥作用的时候了。对于每个给定的区域，我们认为里面的星星数目是个随机变量，比如上面所说的N(A)和N(B)。为了我们的讨论能够继续进行，需要做出一些简化假设。在这里，我们的假设很简单：

1. 对于任意两个不相交的区域A和B，N(A)和N(B)是独立的。

2. 两颗星星几乎肯定不会出现在同一个点上。

对于这两个假设，我需要做些说明。首先，请大家注意，除了说他们独立之外，我没有对N(A)和N(B)的分布形式作出任何假设——后面，我们会看到，为什么不需要假定它们是什么分布。另外，在第二个假设中“几乎肯定”(almost surely)这个术语在数学上是有严格定义的，某个事情“几乎肯定”会发生，表示，它们发生的概率是 1。

了解现代概率理论的朋友对于almost surely想必是司空见惯了。为了让对这个术语不太熟悉的朋友不产生误解，我还是在这里澄清一下。“几乎肯定发生”和“必然发生”在数学上是有所区别的。举个例子，我们在从 [0, 2] 这个区间的均匀分布中随便抽一个数 a，那么 a 刚刚好等于 1 的概率是多少呢？——是 0。所以，我们可以说，a “几乎肯定”不刚好等于 1。但是，我们不能说 a 必然不等于1。

空间点过程

好了，继续回到我们的主题。

这个数星星的例子代表了一类非常广泛的随机过程——空间点过程(Point Processes)。具体来说，什么叫做一个空间点过程呢？我们知道，对于一个（实数值）随机变量，每次抽样（或者试验），得到的是一个实数；对于一个随机向量，每次从分布里面抽取的是一个向量。那么，一个空间点过程，每次抽样得到是在某个空间中的一个离散点集（里面有有限个或者可数无限个点）。在数星星的例子里面，这个空间就是“星空”了。一般来说，这个空间可以是任意的，比如实数集，二维空间，三维空间，曲面，甚至是无限维的函数空间。

最基本的空间点过程，叫做空间泊松过程(SpatialPoisson Process)——一个空间点过程，如果在不相交的区域中的计数是相互独立的，那么这个空间点过程就叫空间泊松过程。虽然，我们没有对N(A)的分布形式作出具体的设定。但是，仅仅凭着不相交区域内计数的独立性，我们就可以得到一个重要的结论：

对于任意的区域 A，在A里面的点的数目 N(A) 服从泊松分布（Poisson Distribution）。

这里说“任意区域”其实是不太严格的——在正式的数学定理中，泊松过程所基于的空间必须是一个测度空间(measure space)，这里的区域A，必须是一个可测集(measurable set)。不熟悉测度理论的朋友可以不妨暂且认为这个区域是任意的吧——因为，在实际常见的几乎所有几何空间里，你能想象出来的集合都是可测集，而不可测的集合只存在于数学家的奇怪构造中。

为什么我们要讨论空间泊松过程呢？它究竟有什么用呢？在我非常有限的知识范围里，我觉得它起码有两个非常重要的意义：

1. 在我们所生活的大千世界里，无数的自然现象和科学观测都可以很好地用空间泊松过程来建模和分析。除了天上的星星之外，还有很多很多：天上飞的鸟，水里游的鱼，街上走的人，空气中的分子，放射过程产生的粒子，桌上的灰尘，很多仪器产生的图像中的黑白噪点。。。。。。
2. 泊松过程是构造很多别的过程的理论根基所在。了解Machine Learning的朋友应该知道近几年，对非参数化贝叶斯(Non-parametric Bayesian)的研究热火朝天——其中很重要的一种过程叫做狄里克莱过程(Dirichlet Processes)。对于狄里克莱过程，大家耳熟能详的也许是Chinese Restaurant Process，又或者是Stick Breaking。可是，您是否知道，狄里克莱过程的理论根源却是源于空间泊松过程？关于这两种过程的联系，是随机测度理论的一个非常美妙的结果。这我们会留在以后的连载中继续探讨。

对于泊松过程，我相信很多朋友不是今天才第一次听说的了。因为，它是很多初级随机过程课程所讲授的内容之一。在初级教科书里面，泊松过程是一个定义在时间上的过程。

时间上的泊松过程用于描述随机到达，比如来排队的人，或者路过的车子。上面这个图回顾了时间上的泊松过程的一些基本的性质：

1. 不相交的时间段上到来的数量是相互独立的；
2. 两个点几乎肯定不会同时到达；
3. 在某个给定的时间段到达的数量服从泊松分布，分布均值正比于时间段的长度。

大部分初级教科书以性质1和3来定义时间上的泊松过程。我们比较一下这些假设和空间泊松过程的假设，就可以看出来，时间上的泊松过程其实是一般的空间泊松过程的特列。这里，泊松过程所基于的空间就是“时间轴”。其实，这里面的性质3，对于定义一个泊松过程不是必须的，泊松分布这种分布形式，其实是满足性质1的必然结果。至于分布均值正比于时间段的长度，仅仅适用于均匀的泊松过程。对于一般的泊松过程，很可能在某些时间来得密集一些，另外一些时间稀疏一些，这时候分布均值就不一定正比于时间段长度了。

上面关于时间点过程的回顾，仅仅是为了说明这篇文章所讲述的内容其实是大家在随机过程课中所学的泊松过程的推广。在下面的讨论中，我们还是回到一般的空间泊松过程。

计数独立和泊松分布

看到这里，我想大家也许会有疑问？为什么不相交区域的计数独立，就必然会导致任意给定区域内的计数服从泊松分布呢？作为一篇博客文章，我不可能在这里进行一个严格的证明。但是，我会尝试从更直观的角度来解释这个结论是怎么来的。这里的背后正隐含了独立计数和泊松分布之间的深刻联系。

为了考察这个问题，我们首先对整个空间进行细分，把它分成很多很小的不相交的小格子。

因为每个格子很小，因此对于每个具体的格子，它里面包含点的概率是很低的，而包含不止一个点的概率就更是低到几乎可以忽略了。因此，每个区域中点的数量，大概等于包含点的格子的数量——这样，我们把数点变成了数格子。

假设区域A包含M个格子，它们包含点的概率分别是p_1, p_2, …, p_M。如果我们用X_i表示在第 i个格子是否存在点，那么 X_i 是一个成功概率为 p_i 的伯努利试验。因而，包含点的格子的总数可以表示为 X_1 + X_2 + … + X_M。因为这些格子不相交，根据不相交区域的独立性假设，X_1, X_2, …, X_M 是相互独立的。在这种条件下，它们的和有一个重要的结论：

对于M个独立伯努利试验X_1, X_2, …, X_M，成功概率分别为p_1, p_2, …, p_M，当每个p_i都很小，它们的总和是个常数C，那么 X_1 + X_2 + … +X_M 近似服从以C为均值的泊松分布。当M趋近于无穷大，每个p_i分别趋近于0，并且总和保持为C，那么在极限条件下，X_1 + X_2 + …，严格服从以C为均值的泊松分布。（熟悉概率理论的朋友应该知道，这样的描述其实是指“按分布收敛”。）

所以，当我们对空间进行无限细分，在极限条件下，会发生下面的事情：

1. 每个格子的大小趋近于零，因而里面包含点的概率趋近于零；
2. 同时，某个固定区域内的格子数目趋近于无穷大；
3. 一个格子内几乎肯定不会出现两个点，因此某个区域内的点数几乎相等于区域内的包含点的格子数；
4. 在这个过程中，某个区域内，所有格子的含点概率的总和维持为一个常数，我们称之为C。

这些观察合在一起可以得到这样的结论：这个区域内的点数，服从以C为均值的泊松分布。如果您熟悉测度理论和依分布收敛的内容，要根据这个思路写出一个严格的证明其实并不困难。

在上面，我们通过独立性假设，建立的泊松过程。其实，泊松过程还可以从另外一个方面去刻画。我们知道，对于某个具体的区域，它里面的点数服从泊松分布（假设均值为C)。根据泊松分布的公式，在这个区域为空的概率（点数为零）是 exp(- C) 。这似乎只是一个简单的性质，但是请不要小看它——就这个小小的性质本身（不需要附加独立性假定），就足以定义泊松过程：

一个空间点过程，如果区域为空的概率随区域的大小（测度）以指数衰减，那么这个过程是一个空间泊松过程。

对于这个事情，它的严格证明需要使用Characteristicfunction的有关理论。但是，尽管不太严格，我们还是可以通过直观的观察对这个结论的原理有所感觉。假定，一个区域的大小（测度）为C，那么如果把它分成很多小格子，每个格子大小（测度）是C_1, …, C_M。那么，显然C = C_1 + … + C_M。因此，这个区域为空的概率有

exp(- C ) = exp(- (C_1 +… + C_M)) = exp(- C_1)  exp(- C_2)… exp (- C_M)

注意，exp(- C_i) 正是第 i 个细分的小格为空的概率。如果一个概率能够按照乘积分解，其实已经在某种意义上预示了，每个格子是否为空其实是各自独立的，也就是说每个格子是否包含点也是各自独立的——这正好吻合了前面我们对泊松过程的构造。

所以，一方面，计数的独立性必然导出泊松分布；反过来，泊松分布其也蕴含了独立计数的内在性质。它们是一对孪生兄弟，谁也离不开谁。

这让我们回忆起概率论中非常著名的“中央极限定理”：大量的独立随机变量的和依分布收敛于高斯分布。（我们上面说的是：大量的独立伯努利试验的和依分布收敛于泊松分布）。如果说，中央极限定理奠定了高斯分布（正态分布）在概率论中的核心地位；那么在空间点过程这个领域，上述的关于独立计数和泊松分布的关系，则奠定了泊松分布在空间点过程理论中的核心地位。

很多的其它重要的随机过程，包括Cox过程，Gamma过程，以及Dirichlet过程，都是以泊松过程为基础的。在后面的文章中，还会进一步讨论我们如何从泊松过程出发构造其它过程，特别是“完全随机测度”(Completely Random Measure)，而统计建模中被广泛采用的Gamma过程和Dirichlet过程，则是这种构造的一个重要的例子。

Postedby dahuasky  |  04月 11, 2010 

冬眠后的苏醒

已是四月深春，刚刚度过漫长冬天的Boston才刚刚焕发出丝毫的春意。这是一个生机勃发的季节，在经历了同样漫长的冬眠后，这个博客也应该苏醒了。

虽然，我自己对于数学依旧深情不减，但是，我发现随着在这个世界里钻得越深，我就越缺乏把其中的深邃的思想用显浅的语言表达出来的能力。我曾经想写Markov Semigroup，想写Completely Random Measure和Gamma Process，又或者Learning中的Abstract Algebra。但是，如果要把它们说清楚，则可能需要洋洋万言的背景介绍——我相信，最多只有三分之一的人能看完其中三分之一而仍然能保持兴趣——这已经是最乐观的估计了。

但是，我还是希望能和大家分享数学的乐趣。但是，以后大家看到的也许是分集连载的“武林外传”，而不是鸿篇巨制的“指环王”。我写得轻松，大家也看得轻松。但是，在今天，我还是先说点别的吧。

众所周知，博士屯的生活——说得好听点是单纯，说得不好听是单调。因此，虽然离开香港快三年了，那个花花世界，那些Good old days，似乎一直让我怀念。寒假回国的时候三度进入香港，让这种感觉有增无减。不过，毕业后可能再也不能如此悠闲的品味这份“单纯”和“怀旧”了，所以，现在还是好好品味一下吧。

“故人西辞黄鹤楼，烟花三月下扬州”。我不是孟浩然，自然也没有李白作诗相赠。不过，在“烟花三月”，“扬州”还是要去的。在刚刚过去的春假，我有幸一睹芝加哥的风采。在刚到的第一天，我对于芝加哥除了凛冽的寒风，再也没有别的感觉——真是名副其实的“风城”。即使住在宾馆里，窗外的呼啸响彻一夜。第二天，特别早就起来了。虽然没有睡好，但是芝加哥早晨清朗的阳光还有连片巍峨的摩天大厦还是让我的倦意一扫而空。（照片已经上传到msn space的相册~~~）

在天际线——这是芝加哥的骄傲，我环拍了25张两千万像素的照片，回去后合成了一个一亿八千万像素的大拼图，放在了PhotoSynth——这个网站提供了方便的用户界面，能让你zoom in到一个巨大拼图的细节观赏。地址是

http://photosynth.net/view.aspx?cid=fc50252d-f90a-496e-ba03-30fb34ae085c

（可能要有高速的网络连接才能流畅的观看拼图的细节。）

出了芝城，我们一直向东穿越，在一天之内，越过了四个州：Illinois,Indiana, Michigan，和Ohio，最后到达Cleveland的附近。在这次旅程中，终于有幸一睹五大湖区闻名已久的玉米地，以及美国的乡村。辽阔的大地总是让人心胸开朗。本来在这次旅程中，我们要去Cedar Point Amusement Park的——美国最大的过山车主题乐园——希望在一天内尝遍乐园内十七座过山车，在尖叫声中暂时抛开生活和工作的压力。不过，最后我们学习到了一个常识：过山车也要冬眠。。。。。。

从五大湖回来后，同样在冬天蛰伏的 IT产业，迎来了一款吸引了不少眼球的新产品：Apple iPad在刚过去的周末正式开售了。虽然，我几乎所有的朋友对苹果的这个产品表示不屑一顾，我还是忍不住在首发日到CambridgeSide的Apple Store去看个新鲜。Apple的很多产品都曾经让我心动不已，不过，iPad确实是个例外。我在店里体验了15分钟，我不得不说这个产品沿袭了苹果一贯的高品质——不过，它缺了一种让我心动的东西。

其实，我一直想买一个电子阅读器——让我能躺在沙发上，或者在飞机上看书和看paper。为此，我关注了Kindle很长时间，不过，它缺了一个很重要的功能，不能方便的在上面写批注——这是我一直以来养成的习惯，从来都是一边看，一边写的。iPad并没有在这方面走得更远，它自带的iPDF只能读，不能写。虽然我相信，很快就会有带批注功能的应用出现——不过，我想要的是一支手写笔，而不是一个手指键盘。。。传说中，微软的Courier似乎能满足我的奇怪需要——它的介绍视频也让我心动不已。不过，它什么时候能横空出世呢？

最后想一提的是，我最近突然喜欢上玩数独（Sudoku）了——因为一个偶然的原因，在等人的时候，为了消磨时间，随后拿了一张报纸，那上面画了一个Sudoku。我解人生中第一个Sudoku花了30分钟——一个题目能让人花30分钟求解显然是非常有趣的，于是我下了一个iPhone版本。三天后，这个平均时间下降到 3 – 6 分钟，而且，我想已经大致明白了“求解的算法”——一个能在计算机上实现的算法。如果一个题目已经到了能用计算机的规则程序求解的地步，它的魅力也就到了尽头，至少我是这么认为的。

一个东西的魅力，在一定程度上源自它的不确定性。游戏如此，做research也是如此。

Postedby dahuasky  |  04月 8, 2010 

写新一年开始的感谢

在2009年，我的生活中发生了很多事情——这一切都已经成为过去了。我在人生道路上每前进一步，都离不开大家的鼓励和支持。我不是一个善于表达情感的人，但是，在这里我想告诉每一位亲人和朋友，你们对我的帮助，我都看在眼里，记在心中。在这里，我要说一声谢谢。

无论在何时何地，我首先要感谢的是我的父母。在这个世界上，父母对于儿女的爱，是最毫无保留的。虽然他们从来没有把这种爱宣之于口，但是，但是我能从他们的一言一行中感受到无处不在的关怀和牵挂。这次寒假回家，看到爸爸妈妈比两年前变老了，心中泛起一种莫名的难过。这让我想起孟郊的那首脍炙人口的《游子吟》：慈母手中线，游子身上衣。临行密密缝，意恐迟迟归。谁言寸草心，报得三春晖。他乡游学，难在父母膝前尽孝，面对年迈的双亲，总是深感愧疚。

然后，我要感谢我的老师们。一直以来，我感到非常幸运的是，在我的学术道路上遇到了几位好导师。在MIT的Eric, John, Alan，还有MSR的Simon，他们在过去一年里为我的研究提供了非常大的支持。Eric的鼓励，Alan的理论引导，还有John和我在具体问题上的讨论，以及在硬件资源上的支持，对于我在研究中排除各种困难，一直走到今天都是必不可少的。在MSR的三个月和Simon的合作，以及他对于工作精益求精的态度，至今让我难忘。

我还要感谢几位在过去一年里给了我很大影响的朋友。出于对他们的尊重，我很少在blog中公开谈论我的朋友们。但是，在这里，我觉得我应该向他们表示我发自内心的感谢。没有他们，我的生活将失去色彩。

鹿茸是我在香港读书期间就认识的。现在，我在美国学习，她在香港工作，但是，我们仍旧是很好的朋友，并且相互关心。在我不开心的时候，她一直都愿意聆听我的抱怨和诉说，并且给了我很多的鼓励和开解，让我一直保持着对生活的热情。

男男和我是很长时间的挚友了。在过去的四五年里，发生了很多很多的事情，我和她的友谊经受了一次次的考验。有些事已经成为了历史，但是，其间的酸甜苦辣都是人生最宝贵的财富。无论发生什么，我相信这份珍贵的友谊是常青的。我祝愿她能得到属于她自己的幸福，祝愿她的生活充满快乐。

婧青是我在MIT的同学。虽然在一个学校学习两年多了，但是我和她之间一直没有什么交往。去年五月，因为专业上的事情，我们才开始熟悉起来。从那个时候开始，这个可爱的女孩给我平淡的生活带来了很多欢声笑语。她的性格非常率真，这使得和她一起玩的时候非常舒服，因为你不用去猜她想什么。我一直有点纳闷的是，以她的急性子，怎么没被我这种缓慢的作派气得吐血，呵呵。

梁菲也是在MIT的同学，是一个很热心的好孩子。她很关心她的学生，也很关心她的朋友们。也许是我和她看问题的角度有不同吧，我和她之间已经吵过好几次架了——超过我和其他朋友吵架次数的总和。不过，我始终信任她——信任她的品格和真诚。我一直觉得，能认识一个像她这样的真诚的朋友，是我的幸运。

陈婧，同样也是MIT的同学，而且和我一样，在CSAIL工作。她的治学态度，学识人品，都是巾帼不让须眉，让我非常敬佩。我特别羡慕她那种纯理论的工作——不用调一个参数，甚至不用写一行代码。对于她，我只有一句话：别老宅在家里了，今天阳关明媚，万里无云，适合旅游~~~~

张维是我在香港时候的老搭档了。我这人做事丢三落四，很多麻烦的事情都是他帮着忙解决的。我求助于他的时候，他从来都是说一不二。哥们之间，感谢的话就不多说了，都在心里了。希望今年能吃上他的喜酒。。。。。。

晓谦是我在CSAIL的同学，虽说贵为公司高管，但是生性随和，待朋友非常热心。自从和他认识之后，就没有少给他麻烦。无论是搬家，还是办宴会，总少不了他的帮忙。祝愿晓谦兄弟小两口子的生活美满幸福。

篇幅有限，很多无私帮助过我的朋友我无法一一列出了。无论如何，你们为我所作的一切，我都心存感激。我们走到一起，共同谱写生命中的精彩，那是我们的缘分，让我们共同珍惜。正因为有了这样的友谊，我们无论遇到了什么样的挫折，都能积极面对，逆境扬帆，也正因为有了这样的友谊，我们对于生活的热情不会熄灭。

Postedby dahuasky  |  01月 17, 2010

deadline过去了

在这个战场上，我不是新来者了。不过这次投paper的感觉和过往不太一样。

 

在其中一篇paper的修改上，Simon和我都付出了很大的心力。从9月下旬初稿完成，到今天最终定稿，两个月内，全文经历了两次几乎彻底的重写，abstract和introduction整个易稿五六次，大小修改不计其数。在paper的最后阶段，我们还有MSR的几位researcher，共同设想了reviewer可能提出的各种质疑，对于觉得解释得不够清楚的地方都逐一重写，直到我们都觉得无懈可击为止。刚才翻看邮箱，发现这两个月内和Simon为了paper的修改来往Email超过了200次。无论从哪个的角度说，这都是我进入这个圈子后，修改付出最多工夫的paper了。

 

在这个过程中，向Simon学习了很多。他对待paper的严谨态度，以及持续不懈精益求精的精神，都让我至为佩服。在我们的通信中，他说的有一席话让我感触很深，大意是：对待每一篇paper都要以best paper award为目标，把paper锻造为高质量的精品。无论最后paper得到什么样的评价，paper的作者都会因为参与了这个高质量的工作而感到自豪。

 

曾经，我为我对于完美的追求感到自豪，可是，这两个多月，我知道还有很多人在这条道路上走得比我远得多。

 

今天有点累了，也许以后会分享更多的经历和感受。

 

 

 

 

Postedby dahuasky  |  11月 20, 2009

悼念钱老

就在刚才，惊闻钱学森先生去世，心情突然变得沉重。钱老是我从小就特别敬重的伟大的科学家，他的为人，治学，以及为国家民族所做的巨大贡献，都是我们共同的楷模。

在此发短文一篇，以表达一个后辈学子的崇敬和哀悼。愿钱老一路走好。

Postedby dahuasky  |  10月 31, 2009

感谢朋友们祝福

 

这个学期因为特别繁忙，已经没有多少时间可以上来写blog了，希望过些时候能恢复吧。

 

昨天，在朋友们的祝福中，我又进入了新的一岁。晚上，做了一个小视频，一方面是对朋友们的答谢，另一方面也在这里和大家分享生日的喜悦。

 

http://people.csail.mit.edu/dhlin/transfer/dahua_2009_birthday_video_1080p.wmv

 

感谢每一位关心和支持我的朋友。

 

 

Postedby dahuasky  |  10月 25, 2009 

再见，西雅图

这个暑期的internship最终圆满落幕。几个小时后，将乘飞机返回久别的校园。

Postedby dahuasky  |  08月 30, 2009

关于高性能数值运算

经过一个月的繁忙后，在Microsoft Research的工作进入收尾阶段。于是，也有时间上来写点东西了。在微软intern期间有很多的收获，等回到学校后，回顾整个过程，再写个总结吧。这篇blog里，主要说的是一个实用的东西，就是在一般的程序设计中进行高性能数值运算的问题。

数值计算是我们实现算法过程中必不可少的部分，在大规模计算中（比如在大型数据集上训练模型，或者在多节点的网络中进行统计推断）对计算性能的追求是非常必要的（在关键环节的优化甚至能把实验时间缩短10倍以上）。对这个问题的思考其实事出有因。一直以来，在学校里面都是使用matlab作为主要的计算工具，可是，到了微软之后情况发生了很大的变化——

在外面看来，微软虽然是很有钱的公司，不过并不是对什么事情都这么慷慨的（个人觉得MIT在不少地方比微软慷慨得多～～嗯，除了工资）。在Redmond的研究院有几百名正式的研究员，外加几百intern；而matlab的license只有30个，换言之，就是整个研究院范围只能同时开30个matlab进程。每天在公司的邮箱里，总能收到很多请求别人release matlablicense的邮件，语气之恳切近乎哀求。在这样的条件下，我的mentor跟我说：matlab is simply not an option。在这种情况下，必须在脱离matlab的环境中寻求高性能计算的其它途径。

从MATLAB矩阵乘法到BLAS dgemm

事实上，无论是在matlab，还是在别的语言下的计算库，高性能计算过程都大概包含了三个层次。为了说明问题，还是以matlab中的矩阵乘法为例子说起。

在matlab中，我们要计算两个矩阵 A 和 B 的乘积，我们会在命令行或者m-file里面写 A * B。这么一个简单的语句是如何转化为实际的计算过程的呢？ 首先，matlab的解释器会分析这个语句的语法，从而知道你要做的是计算 A 和 B 的乘积。但是，matlab其实只是个外包装，并不是自己进行这个计算的，而是把计算过程委托给一个核心的C语言计算函数叫做dgemm，然后dgemm进行实际的计算，最后matlab对dgemm输出的结果重新打包返回。

这个名字很奇怪的函数究竟是怎么回事呢？它其实是BLASLevel 3中最重要的函数 (常用BLAS/LAPACK 或者 MKL的朋友对这个函数肯定不陌生)。BLAS全称 Basic Linear Algebra Subprograms，它是在1979年被提出的来用于支持建立一个叫做LAPACK的矩阵代数的运算库。到了今天，BLAS函数已经成为矩阵和向量运算的事实上的“国际标准”接口。BLAS的函数分为三个Level, 

Level – 1是向量和向量之间的运算，比如点积 （ddot)， 加法和数乘 (daxpy),  绝对值的和 （dasum)， 等等；
Level – 2 是向量和矩阵的乘法运算，最重要的函数是一般的矩阵向量乘法(dgemv)
Level – 3 是矩阵和矩阵的乘法运算，最重要的函数是一般的矩阵乘法 (dgemm)

dgemm这个名字是什么意思呢？其实全称可以翻译为 double-precisiongeneric matrix-matrix muliplication.其实，Level-3虽然只做一件事情，就是矩阵相乘，但是，它还有很多其它的函数：比如sgemm (单精度一般矩阵乘法)，dsymm(双精度对称矩阵乘法)，zhemm(双精度复数埃米特矩阵乘法)，诸如此类还有很多 。。。。。之所以要分成这么多种，主要是针对每种不同类型的矩阵，都要分别针对性地设计专门的算法使得对它的性能尽可能的高。

另外还有一套同样著名的标准运算接口，叫做LAPACK(LinearAlgebra PACKage)，它是基于BLAS的基础上建立的线性代数运算库，提供一些更复杂的功能，比如LU, QR, SVD分解，或者求解特征值和特征向量，又或者求解线性方程组以及最小二乘法等问题。

其实 BLAS 可以理解为只是一套函数接口，在遵循接口的情况下，不同的库可以有不同的实现。很多著名的软硬件厂商都分别实现了针对自己产品专门优化过的BLAS实现。最著名的实现有下面一些：

ATLAS:  这是一套开源的实现。很多开源的数值软件都使用ATLAS优化的BLAS；
Intel MKL：这是Intel针对它的CPU系列开发的核心数学运算库，提供了完整的BLAS和LAPACK实现，除此以外，还有很多功能；
AMD ACML： 作为Intel的长期对手，自然也不甘人后；
Sun Performance Library:  主要针对Sun的SPARC架构；

另外，Apple, HP, NEC都有各自的BLAS实现。各大芯片厂商其实都不遗余力地提高自己的BLAS实现的性能——因为，前面提到的那个著名函数dgemm的运算速度是衡量一个CPU数值运算性能的非常重要的指标。一般来说，我接到一台新的机器，都会打开matlab算几次1000*1000或者2000*2000的随机矩阵乘法（前面提到，matlab也是调用核心的dgemm做这个事情），这样我就大体知道这台机子的数值性能了。

既然大家都实现了BLAS，为什么我们通常不直接用它呢？答案很简单，太不方便了。dgemm这个函数做矩阵乘法，一般可能觉得它会有三个参数，两个输入，一个输出。考虑到需要把大小信息m, n, l 也提供进去，最多6个参数。好，我们一起来参观一下这个C函数的声明：

void cblas_dgemm(const enumCBLAS_ORDER Order,
                const enum CBLAS_TRANSPOSE TransA, 
                const enum CBLAS_TRANSPOSE TransB, 
                const int M, 
                const int N, 
                const int K, 
                const double alpha, 
                const double *A, 
                const int lda, 
                const double *B, 
                const int ldb, 
                const double beta, 
                double *C, 
                const int ldc);

总共14个参数。不知道大家是否有心情在一般的算法开发中用这东西做矩阵乘法，反正我是不会这么做的。而matlab这类软件的好处是包装了这些很难用的函数，使得我们在很愉快的写A * B这样的表达式时，同时享用BLAS带来的高性能。

让矩阵乘法变得更快

我们都知道矩阵乘法的运算规则，其实很简单——一个10行内的的三重循环就能实现。为什么那么多大公司还要年复一年的研究怎么算矩阵乘法（还有别的更简单的数值运算过程）呢？因为，算对很容易，算得快却非常艰难。通常来说，会使用这么一些技术：

－ 分解小矩阵块，每个小块都用特殊优化过的算法计算；
－ 把循环解开，减省内重循环中用于更新循环变量的开销。对于矩阵乘法这样的高密度数值运算，内重循环中每次循环哪怕减少一个指令周期，对整体性能都是很大的提高；
－ 对高速缓存（Cache）的调度进行改进，提高命中率；
－ 充分利用指令流水线，使得数据的读取，计算，写入这些接续操作在流水线内同时进行；
－ 使SIMD指令集（通常是SSE, SSE2, SSE3等）。SIMD全称是Single Instruction Multiple Data，就是一条指令在单周期内处理多组数据，在新的CPU中都支持这些指令。

SIMD对于向量运算的加速有重要意义。举个例子，在SSE2有指令能在单周期同时对一组128位浮点数（两个double，或者四个float）进行加减乘除或者开平方运算，可以想见，充分利用这些指令能对计算速度成倍提高。对于不同的CPU，不同的架构，不同大小的矩阵，对这些技术的运用也不尽相同，因此最终形成的实现算法非常非常复杂——资料显示，现代CPU上高度优化的矩阵乘法实现不是10行以内的for-loop，而是超过10万行！其中包含了大量和CPU和Cache密切相关的东西。

归纳起来，高速矩阵运算的全过程包含三个层次：
1.  上层封装好的接口： 比如matlab里面的A* B;
2.  中间层的 BLAS/LAPACK 的 C 函数，像dgemm，它们通过非常复杂并且硬件相关的技术来提高速度。
3.  这些C函数会调用CPU中的指令进行运算，其中SIMD（SSEx)指令集对于运算速度的提高有着关键意义。

提高基本运算的速度显然不是我们的任务，Intel和AMD的工程师会管这个事情。对于我们来说，合理的做法就是拿来主意，让他们开发出来的技术来提高我们的实验效率。如果能用matlab，matlab已经把这个包装好了。如果你是那种对性能特别有追求的人，那么你可以到Intel或者AMD的网站获取最新版的MKL或者ACML，安裝到你的机器上，然后设置BLAS_VERSION环境变量就能让matlab使用最新的高性能库了。

其它的常用数值软件，比如Mathematica,numpy, Octave, R都提供了方法链接不同的BLAS实现。对性能关键的数值运算程序，在选用支持库时，能否接入高性能BLAS实现是一个重要的标准。如果两个库都使用同一种BLAS实现，那么它们的计算性能应该是差不多的（除了在封装层的overhead略有差别）。而接口封装的质量当然也是重要的考虑，这直接关系到它的易用性——这方面matlab是我见过做得最好的，Octave的接口仿造matlab，不过octave的运行环境比matlab就差多了。numpy和R都存在类似问题。

－－－－－

至于我自己，在微软intern期间，按照自己的设计思路重新用C++设计了一套新的矩阵库（这不是我在微软的主要工作，只是磨刀不误砍柴工而已），主要的设计目标有两个：(1)向下为接入MKL之类的BLAS/LAPACK实现提供方便；(2)向上对用户 提供类似matlab的接口。同时也利用这个机会探索一些有趣的C++ template metaprogramming的技术。在微软写的代码自然是不能公开的。不过，我每天回到住处后又改进设计思路重写了一套（这套就不属于微软了），准备带回学校后继续使用。在经过一段时间考验后，我想可能会把源代码开放出来和大家交流。

Postedby dahuasky  |  08月 15, 2009

旅程匆匆

在过去的一个月里，生活中充满了繁忙的气息。除了研究院的工作，还有接踵而至的旅程。

6月12日：游览Olympic National Park
      时值初夏，山上依旧白雪皑皑，与蓝天绿草交相辉映。

6月21日－6月25日：到迈阿密参加CVPR 2009
      可惜没有到外面旅行，只是在宾馆里和香港的老同学叙旧。

7月17日－7月20日：加州之旅
      7月17日：抵达Palo Alto, 在当天下午参观Google总部和Stanford校园，并且和在Stanford学习的朋友们聚餐
      7月18日：到San Francisco游览。浓雾中的金门大桥别有一番情致。特别感谢Xie Yao 和 Ma Li 的热情接待。
      7月19日：抵达Pasadena (Caltech的所在地)。Xiaodi的“开水白菜”，至今回味无穷～～
      7月20日：参观Caltech校园，晚上返回Seattle

7月24日（今天）：到Denny Creek Trail Hiking
      从早上8点出发，到晚上7点才回到。和香港的麦理浩径相比，这里的登山道更为险峻难行——到处都是大小各异的碎石。雾很浓。青山绿水在雾中若隐若现，如水墨画一般。

关于这些旅程，已经上传了五个相册：
Olympic National Park
Visiting Stanford University
Visiting Caltech
Visiting San Francisco
Denny Creek Trail Hiking

这些相册同时传到msn space和google picasa:http://picasaweb.google.com/lindahua

今天实在太累了，需要早点休息。以后有空，再补上详细的游记。这里再次感谢在加州的兄弟姐妹们的接待！

Postedby dahuasky  |  07月 24, 2009

对Research的新思考

在MSR已经工作三个星期了，这几个星期过得很充实。除了一些细节还有待推敲之外，整个framework的formulation已经基本成形。

让理论在解决实际问题的挑战中展现风华

在这里，我接触到是一种和在MIT时很不一样的研究方式，这让我对research有了新的思考。在学校的时候，理论上的思考是占据主导地位的，我和我的advisors更关注对于理论的发展，而对于如何把新的理论工作应用在实际问题中，虽然也有一些大体的想法，但是，往往是比较模糊的。而在微软，虽然研究院的研究和产品部门相对独立，但是，大部门的研究还是以应用为基本出发点的。在这里，大家往往首先考虑要提出一个什么样的新应用，而理论和数学工具的选择则处于从属地位。其实，这种应用导向的研究思路，我在五年前在MSRA工作时已经经历过了，不过在学校注重理论氛围中，已经有所淡忘了。

其实这两种思路并没有属优属劣之分，它们各自对于领域的发展都是有着不可替代的作用的。虽然我个人的研究风格更倾向于理论，但是，这几个星期和这里的研究者讨论的时候，也越来越觉得，在研究过程中贯彻对于应用的思考也是同样重要的。首先，计算机视觉本身是一门应用科学，各种理论存在的价值最首要是体现在它解决实际问题的能力上，而并不是理论本身是不是好看。很多朋友都有理论审美情结，喜欢欣赏高深漂亮的数学演绎，并或多或少地以此为标准评价一件工作。我也有着这样的审美情结，直到今天还一直坚持为建立更好的理论而努力。不过，我越来越认为，

真的要实现一套新理论或者一个新模型的价值，除了要赋予她深厚的内涵，更需要在应用领域中为她寻找一个让她充分展现风华的舞台。

在构建理论模型的过程中，为了导出符合某种要求的结果（比如要求objective function是convex之类，或者能得到某种漂亮的闭合解），往往需要做出各种或明或暗的假设。而很多这样的假设，会导致模型在一定程度上偏离真实问题。在理论和实际中做出某种折衷，有时是不可避免的。如果缺乏对实际问题的关怀，那么人们很可能在审美情结的驱动下在偏离实际的道路上越走越远，失去应有的平衡。然而，

理论只有离开充满假设的温室的呵护，到实际问题的世界中接受考验，才能真正地成长。

我们向资深的学者学到的最有用的东西，并不是某种具体的数学方法，而是在面临这些问题时，如何从更高的层次去预见各种不同的选择的利与弊，以及如何综合考虑各种因素后做出一个明智的决定。虽然，我们在一开始设计一种理论模型的时候，往往会从简单假设出发，以后在把它应用到更复杂的问题时进行扩展。一套有生命力的理论，往往有着一种灵活而健壮的内在机制，使得它们的应用范围能很方便地在实践中不断拓展；而相反，一套设计不良的理论，即使在开始很漂亮，在扩展的过程，需要加装各种不伦不类的补丁而愈发变得丑陋，很快就不堪重负而走到其生命的尽头。

虽然这里我强调对应用的思考的重要性，但是，我并不因此认为数学在计算机视觉的研究中就不再重要了——在微软的经验并没有让我放弃在理论上的追求。而是让我在纯理论道路越走越远的过程中重新认识到应用思考对于理论研究的意义，并且开始认真思考如何让自己的理论工作在解决新的实际问题的过程中发挥作用的问题。

 

从不同的研究风格中学习

这几年，我有幸到不同的地方进行研究，接触不同的研究风格。对比现在和三年前的自己，我觉得，一个很大的变化，就是学会了尊重不同的研究风格。以前，出于对漂亮而严格理论的偏好，对各种在实用系统中使用的工程方法不屑一顾，认为没有“学术价值”。之前一些理论工作，在和别人讨论，或者在paper review中受到质疑，往往自然生出对质疑者的反感，必欲强烈反驳而后快。在经历很多经验教训之后，才慢慢认识到，尊重质疑自己工作的意见是获得进步的开始。

自己付出很大努力做出的一项工作，当然希望得到大家的好评。但是，自己的思考往往受背景所限其实是不全面的，质疑者的看法也许也同样是不全面的。但是，他们可能是从另外一个角度来思考，发现这个工作的不足。如果能认真思考他们的（哪怕是有偏颇）的意见，就能使这个工作变得不断完善。有时候，质疑的原因是因为理解错误了，我觉得，研究者这个时候首先应该考虑的不是质疑的人是否理解能力不够，而是自己的表达是不是不够好，可能容易引起别人的误解。对于，别人的意见虽然不需要全盘采纳，但是在对每一种不同的意见都进行认真的反思，则是很有价值的。

不同风格的研究者，在评价一项工作时的价值取向时往往就存在根本分歧。一种常见的情况是，研究者对某个传统的问题提出了一种很新的理论模型。这样的工作在一个应用背景很强的人看来，可能只是很小的贡献，因为它并没有解决新的问题，而理论的新旧只是一些细节的变化（在我接触的一部分做应用系统的研究者眼中——理论部分只算是一种detail）。这样的评价也许有失偏颇，但是并非全无道理——在一个已有模型已经能解决的问题上，为什么要再换一套理论呢——用汤老师的话说：

“用英语说过的话，就不必用拉丁语再说一遍了”

如果评价者存在这样的印象，就可能表明这项工作存在一个重要的不足：没有搞清楚究竟解决了什么新问题——而这恰恰是一项理论的价值的根本所在。虽然不是每篇文章都能开辟一个新的topic，但是即使是做传统topic的文章也应该要解决这个topic已有方法解决不好的问题。究竟一项工作解决了什么问题，研究者有责任旗帜鲜明地指出来，并且用令人信服的实验来证明。而空洞的claim或者让人云遮雾罩的理论演绎并不能有效地彰显这一点。

在MSR工作这些天来，一些和我合作的研究员的研究风格有很大差别。我开始提出一个framework自我感觉良好，但是在和他们的讨论中，我发现它还存在各种不足，而在不断吸收他们有价值的意见的过程中，这个架构变得更加严谨和符合问题的真实情况。并且这种交流的过程促使我对research的方式进行了新的思考，这也是我这次Intern的一个重要的收获。

Postedby dahuasky  |  06月 21, 2009

Olympic National Park

这个周末，微软组织research intern到Olympic National Park游览。旅途很累，基本三分之二的时间是在车上度过的。不过能一览胜景，也就值得了。全程拍了两百多张照片，上传了一部分。大家看图好了。

Postedby dahuasky  |  06月 14, 2009

MSR的工作环境

终于度过了internship的第一个工作周，这是一个充实而富有收获的星期。

我不是第一次在微软实习了（上一次是五年前在北京），不过这一周的工作还是让我觉得有点新鲜，因为这里和MIT还是有很大差别的。

这里先说说工作环境吧，在我来之前，这里的工作人员就为我分配了一个办公室（一般每个办公室有4个intern student），并设置好一台电脑。所有intern用的电脑都是一样的标准配置：3.2 GHz x 2的dual core CPU,  4G Ram，和22寸宽屏液晶显示器。大家的电脑里面装的都是Vista Enterprise，以及其它微软的软件。这两年在学校一直使用LinuxWorkstation，把工作环境换到Windows下开始还真有点不习惯。于是，第一天就把cygwin，emacs, vim之类的东西装上，算是仿冒了一个Linux环境吧——我还没这个胆量在微软的老巢把Windows卸了，装个Linux。后来，我mentor进来跟我说，其实他也装了cygwin + emacs ~~~。不过，为了表示对微软的尊重，改用IE + Bing，而不是Firefox + Google了。

总体来说，Microsoft Research和MIT CSAIL相比较，在工作条件上各有千秋：

• 两者都有一个统一而且功能丰富的内部网络，不过分别以Windows Server和CSAIL Debian为支持。总体来说，感觉CSAIL所使用的AFS系统在文件共享方便比Windows要方便一些，也许是因为我自己这两年用惯了。
• 两者都有专门的IT支持部门。从这个星期的经验看来，Microsoft的IT部门的反应效率远比CSAIL的要高。
• Microsoft内部可以使用微软自己的全线产品和很有限的微软以外的软件，而CSAIL内部则提供Microsoft的主要产品，以及很多其它软件。所以这几天在微软发现很多自己平时常用的软件都不available了，比如Acrobat；MATLAB可用的工具箱也少了很多，而且license比较紧张。
• MSR里面intern使用的打印机只能支持黑白打印（据说彩色打印需要高层主管的批准），而且打印质量很一般。而在CSAIL每一台打印机都支持质量很高的彩色打印，而且对学生没有任何打印限制。这几天看黑白的paper还有点不太习惯。
• 平均来说，CSAIL的Vision组学生自己使用的工作站的配置要明显高于MSR Intern的标配。但是，MSR有着非常强大的计算资源：拥有超过8000个核的大规模计算集群，CSAIL的公共计算能力比这个起码差一个数量级——其实CSAIL的总计算能力还是很大的，只是每个组各自为政，始终没有搞出一个非常强大的公共集群。
• 微软的饮料是免费的，而CSAIL就没有这种福利了，呵呵。

Microsoft Research应该说是industry lab中最接近学校模式的实验室了。没有固定的上班时间，除了和mentor约好的meeting时间外，其它时候去不去或者什么时候去上班都是个人自己的自由。只要把工作做好就行了。而且，研究的选题是以topic本身的学术价值为首要标准（比如这个题目是不是interesting &novel)。如果这项研究和微软的产品有关系当然好，如果没有直接联系也无所谓。

相比于MSRA，在Redmond总部的研究院的mentor/intern比例是比较高的，我们组平均每个researcher只有不到一个intern。我所在的Interactive Visual Media Group今年暑假一共有7个intern student，其中5个来自MIT，另外一个来自Harvard，还有一个是Cornell的。

工作条件的差别只是其中一个方面，通过这个星期和这里的researcher的接触，我感觉到在对问题的思考方式上也有着很多有趣的差别。接触一种不同的思维方式其实是这次internship的一个重要的收获，关于这个方面，以后再找机会细说。

Postedby dahuasky  |  06月 6, 2009

首访微软总部

今天早上起来后，决定到微软走走。于是带着相机出门了。

六月的Redmond掩映在一片绿色之中。树丛深处花团锦簇，春意盎然。从我的住处步行到微软大概需要半个小时。微软的main campus像是一个大公园，既没有很多高科技企业那种现代感，也没有古典名校的庄重感。走在这个campus中，让人感到宁静而悠闲。

在一路上，我拍了很多照片。已经选出一部分上传到相册之中和大家分享了。

Postedby dahuasky  |  05月 31, 2009

到达Redmond了

昨天晚上（噢，应该是今天凌晨）收拾到四点多，还没来得及打个瞌睡，五点半的时候就出发到机场了。经过六个小时的飞行，在西岸时间十一点到达西雅图机场，最后到达宾馆的时候已经是这边的中午了。

Redmond是一个花园城市，看上去感觉很舒服。不过今天中午太阳太毒了，吃午饭时在外面走了一会就热得受不了。实在太困了～～～先去睡觉了，睡醒后继续update。。。。。。

这一睡醒来的时候，已经是晚上八点了，不过外面天色还很亮。外出吃晚饭的时候，沿着24St散步，发现这条街道麻雀虽小，五脏俱全，各国风味的餐厅都有，还有一个中国超市——终于明白为什么小刚在这里呆了一个暑假，回去后胖了两圈。。。美中不足的是，shopping mall远了一些，开始怀念Shaws Market和Galleria。

这个周末先在住处好好休息一下，下周一早上就要正式开始intern的工作了。希望在这里能认识很多新的朋友。

Postedby dahuasky  |  05月 29, 2009 

五月的最后一周

在这个星期五的早上，将要踏上去西雅图的班机，开始新的intern生活。

关于Thesis Proposal

前段时间因为牙疼~~research上有点怠工了。不过，前两天终于完成了一件最重要的任务——撰写Thesis Proposal。paper写过不少了，但是写proposal还是第一次。虽然proposal不需要评分，也不需要peer review，不过，这确实是一个非常有挑战性的过程——因为它不是要把已经做好的东西写出来，而是要构思你将来要做的东西。利用这个过程，我重新思考了我所做的研究。

在过去的一年里，主要是在微分几何和李代数的基础上建立动态过程的表达体系，这个理论工作在很大程度上统一了以往在motion analysis中所使用的各种描述方式，并且能够使用代数方法对运动进行合成和分解。我一直坚信这项工作是很有价值的，但是，最近几个月来，我发现我对于这样一个问题始终未能给出满意的答案：这种新的方法论究竟有什么实际意义？或者说，它能解决哪些以有的方法不能解决或者解决不好的问题？计算机视觉是毕竟一门应用科学，一套理论的价值最终是要体现在应对实际挑战之中的，如果一套新的理论不能解决新的问题，就成为无源之水，无本之木，失去了存在的价值。

在CSAIL的内部交流中，有一位老师提出了这样的疑问：如果一个问题能用传统的更加直观的方法解决得不错，为什么需要采用这种看上去比较抽象的代数方法，仅仅是因为数学上更加漂亮么？在当前的实验中，新方法确实能带来结果的改进，但是，我觉得传统方法经过适当修改后，还是可能取得类似的改进效果的。因此，我始终觉得这样的improvement并不能真正地说明新方法的意义。要真正确立新方法的价值，就需要找出这样的问题：传统方法有着根本性的困难，而这种困难能够被新方法有效克服。对于这个事情，我思考了很多，有一些初步的想法，但是，要实现这样的目标，还需要付出很多的努力。

关于ICCV 2009

Review的意见已经公布了，最后的录用结果要到6月才会出来，祝大家好运。

我为这次会议review了一批文章，大部分是关于face recognition或者object recognition的，review结果公布后，我也看到了其它reviewer对这些paper的评价。再最近几次的computer vision的会议中，我都发现了同样的一个现象。很多作者仍旧在乐此不疲地做各种改进版的PCA，LDA，或者它们的2D版，又或者kernel版。这些文章在方法上大同小异，就是对matrix进行某种regularization，或者对objective function或者优化过程稍作修改，结果上相对于标准实现略有改进。而且文章的撰写套路也差不多。

我和小刚几次讨论了这个现象，都觉得这样的paper已经有发展成“八股paper”的倾向。我问了一些参与review的朋友，也对此感到厌烦和无奈。从我了解到的小部分review意见看来，reviewer对这种paper的批评已经趋于严厉，很多都给了definitely reject的评价。我现在基本不怎么做recognition了，但是，对于做recognition的朋友还是有个小小的建议：如果可能的话，在选择methodology或者topic的时候，尽可能避开那些重复建设已经泛滥成灾的方向吧。

Postedby dahuasky  |  05月 26, 2009

投入iphone的阵营了

一个月前Verizon的Plan到期了，考虑了好长时间（其实就是憋了很长时间，忍不住了~~~~），今天终于跑去AT&T签了两年的“卖身契”，换回来一台 iphone 3G。

不多说了，大家看相册吧。

Postedby dahuasky  |  05月 15, 2009

上完第一次数学课

决定选数学作为minor，从这个学期开始会上一系列的数学课。这个学期选的是Real and Functional Analysis，这门课已经进入尾声，下周就要考试了。

这门课主要讲的是测度论和勒贝格积分理论，以及一些基础的泛函分析，这些内容自己以前也自学过，不过经过一个学期的学习，还是觉得有不少新的收获。

由于老师讲课没有依据特定的教材（这似乎是MIT的风格，我在这上的所有课都没有特定教材的），而且连lecture notes都没有。我的做法是在堂上记下笔记，然后每周都抽出时间把笔记用Latex整理成Notes。事实上，这些整理出来的Notes我在整理完后已经不太需要看了，真正发挥作用的是这个整理的过程，它对于知识的吸收起到了很重要的作用。

一方面，老师上课比较“即兴”，讲的时候很多东西都是穿插着讲的，并不依循一个特定的逻辑顺序，所以在整理的过程中，就需要充分理解上课所讲的材料，理清它们的关系，然后重新归纳出一个合乎逻辑的顺序。另一方面，由于时间很紧张，很多定理和命题，老师都没有给出证明，这些证明我都在整理笔记的过程中自己独立完成了。回头看来，这个过程其实使自己受到了一个充分的数学训练——相当于把整个体系从头到尾推导了一遍。很多概念，定理，以及它们的关系，在这个过程中被充分消化了。

以前自学完后，感觉自己对这些科目的把握还是有点虚；但是，经过这一个学期的学习后，尤其是当动手，在不依赖参考的情况下把所有东西推导一遍之后，感觉掌握得比较实在了。我想这和学习programming是有类似的地方的。比如一个人拿着几本C++或者Java的经典教材啃了一遍之后，让他完成一个non-trivial的程序，他未必能轻易地架构出来；但是，如果他在一个实际工程中写了10万行代码，情况可能就很不一样了。知识和技术都是需要在实践中去深化的。

下面再说说这门科目本身吧。测度，积分，泛函在一些人看来可能听上去挺深的数学，但是，它们其实是分析中最基础不过的部分罢了。学完这些，我想也就是属于刚刚踏入分析的门槛。可是对于非数学专业的学生，学习它们的作用究竟是什么呢？直接用测度论的某定理搞出一个模型去发计算机的paper？这个想法虽然不能说是完全不可实现，但是起码是不太靠谱的。我个人的看法是，学习它们的意义主要是培养数学分析中的思维方式，同时也为学习一些以它们为基础的专门学科打下基础。

在我看来，分析中最重要的思想，就是极限和逼近。这种思想其实我们高中学习极限时就开始接触了，但是可能是课程设计的原因，在大学微积分中，更多的是强调求导，求积分，解微分方程等的技巧，反而对最根本的极限思想没有足够的重视。我在一些数学论坛上，经常看到对于某些数学概念的激烈争论，这些争论相当一部分其实是源于某些参与辩论的人对极限的思想缺乏正确的理解。在测度论和泛函分析中，极限和逼近的方法被广泛运用在各种概念的建立和定理的证明过程当中，因此学习这门学科的过程对于深入理解现代分析思想是很有意义的。

另一方面，学习这门课是为了进一步学习现代概率理论，高级随机过程，和随机分析理论打下基础。这些东西以前也学习了一部分，但是感觉还是掌握得不实在，打算通过修读下一学年的数学课作更深入的学习。因为我研究的主要方向是对于运动的建模，涉及动态过程的随机模型，由于受到数学的限制，在一些理论探索中常受到约束，很难进行更深入的发掘。希望通过这些数学的学习，为进一步的理论研究打下基础。

这个学期上课的Notes都整理出来了，有兴趣了解这门课的朋友可以参考一下。

http://people.csail.mit.edu/dhlin/measure/cnotes_mi.pdf

Postedby dahuasky  |  05月 3, 2009

Some recommendations

推荐两个东西，希望对做research的朋友有帮助。

1. Mendeley

一个paper管理软件。像我这种paper下载下来都就到处乱丢的人，这个小软件帮了我不少忙了。最近在写thesisproposal的时候，我用它整理了散落在计算机各处的paper，觉得非常方便。

相比于其它类似的软件，它有几个好处：

• 跨平台，对于Windows, Linux和Mac都支持。
• 提供了一个网上存放paper database的空间，所有经它整理的paper，都可以同步到网上。于是使用者就可以在不同的电脑上查看一个updated的paper库~~ 有点svn的感觉，呵呵
• 提供了多种不同导入paper的方法。还有一个查找paper的功能，这个我在写review的时候感觉很不错。
• 免费 ~~~ 这个最重要了
• 可以在不同使用者之间share paper。

软件主页：http://www.mendeley.com/

2.  Graphical Models,Exponential Families, and Variational Inference

这是Wainwright和Jordan近期的大作。全文305页，是关于这个Graphical Model和Variational Inference的很全面的教科书。书中对于这方面的内容，以及它们和Convex optimization的联系有很深入的探讨。

新学习这方面内容的朋友可以以此为教材，即使是熟悉这方面内容的也可以温故而知新。文中有很多鞭辟入里的见解，而且对于各种理论之间联系的发掘很深入。

此文发表在Foundations and Trendsin Machine Learning上。目前可以免费下载pdf。它也以书本的方式出版了，不过价格不俗，$125。

Website:  http://www.nowpublishers.com/product.aspx?product=MAL&doi=2200000001

Postedby dahuasky  |  04月 27, 2009 

和导师的interaction

前两天和Yaoyao讨论了很长时间关于和导师交流的问题，感觉这个讨论的过程很有收获，在这里和大家分享一下我的一些看法。

这个事情其实是因人而异的，老师指导风格不同，和他互动的方式也就不一样了。Yaoyao在Stanford接触的老师的风格和我在这的导师的风格就大相径庭。不过，我觉得有一些基本的经验在不同的地方都是有用的。

对于PhD的研究来说，一般是强调自己的探索，不过导师对这个过程也是起着关键作用的。是不是能和导师保持良好的合作，在一定程度上会影响着研究的成败。我很庆幸自己从开始学术研究以来一直都遇到很支持我的导师，因此，我才能在这条道路上走到现在。

在如何和导师互动这个问题上，我自己也尝试过不同的方式。在读Master的时候，由于汤老师长期在北京，我和他见面的机会很少，所以基本上从选题到最后的论文，都是自主的把握。很多情况下，汤老师会到paper写完那时候才会知道我究竟干了什么。那时候，在每次会议deadline前，都会写多篇paper，而且是不同topic的。虽然，最后paper发了一把，也拿到了自己理想的offer，但是真的很惭愧，那时候做的事情，也许并不是真正意义的Research。不过，虽然谈不上多少贡献，但是在那两三年里还是有不少收获的，看了很多文章，对这个领域有了比较多的了解，懂得了这个圈子的一些游戏规则，积累了一些写paper的经验。

到了MIT以后，对于新的研究环境，我开始时很不适应，过了相当一段时间后才把握了和导师们合适的互动方式。

最首要的一条，就是必须有一个稳定的研究课题。在以前那个时候那种为了会议临时挖坑，东一榔头，西一锤子的策略，是不能获得导师的认同的。导师一再强调，所有的研究要以最终的PhD Thesis为目标，在这几年时间内完成一项能产生真正影响的工作。几位导师都曾经多次敦促我尽快写thesis proposal。他们很鲜明地反对那种在临毕业前才开始写thesisproposal的做法。原因是，一个proposal能对未来的研究提供清晰的导向。我曾经困惑，在研究初期撰写thesis proposal会不会给后面的探索带来限制，也向我的导师们表达了我的担忧。他们的回答是，proposal是一种很大体的设想，它的作用在于帮助你在研究开始的时候就对后面的道路进行初步思考，使得研究不至于陷入盲目，并且尽快走上正轨。而具体的走向会有很多unexpected的变化，甚至完全超出proposal的预想都是可能的也是允许的。

我每周都需要和不同的导师meeting，这是他们了解我的进展的主要方式。我越来越感到和导师密切沟通是非常重要的。只有他们真正理解了你的想法，才能对你的研究给与支持，也才可能提出由价值的建议。我的导师们都强调的研究的延续性，没有充分讨论之前就突然变换课题的做法是肯定得不到支持。研究其实是一个充满不确定性的过程，他们也了解这一点，所以鼓励自由探索，不过如果要发生重要的研究路向的改变，则需要有充分的理据的支持。每次开会开始时，在讲述自己新的进展之前，我都会说明我为什么需要这些新的东西，它们和原有的东西有什么联系。当我把这些解释清楚了，基本上都能得到导师的支持和鼓励。

导师也常常会给出它们的建议，很多时候这些建议都很有价值。事实上，很多我现在很多新的进展都得益于从他们的建议中获得的灵感。但是导师的建议并不一定是最好的或者是可行的。对于自己做的课题，自己肯定比导师更加清楚。所以，这些建议要区别对待。特别值得一提的是，有些建议虽然整个看上去不太可行，但是某些方面上其实体现了很好的思想。那么，就可以想办法吸收那些好的想法，和去掉不可行的部分。这种再分析之后进行扬弃的过程，比起全盘照搬，或者全盘抛弃都更为有效。对于好的建议，应该对导师表示谢谢（比如向他说一句Thank you），而对于不可行的部分就应该当面和他解释清楚。有些时候，如果一些分歧在短时间内不能达成共识，我一般会提出在会后再深入思考，其实，很多这种分歧都在进行新的思考后得到很好的解决。

至于会议进行的方式，我也是经历了一个逐步转变的过程。刚来的时候，一方面怕自己口语不足以临场发挥，另一方面觉得meeting都是很正规的场合，所以都准备好presentation，然后在meeting上很正式地讲。后来发现，每周meeting都这么做，时间开销上实在吃不销，于是开始放弃预先准备的方式，发现其实讲得也还可以。于是，以后就都改用informal的讨论方式了：就是开会前花10分钟在心中整理一下要讲的要点，然后meeting的时候，直接站在白板边上，边写边讲。由于没有ppt的约束，很多时候通过这种方式和导师的讨论更加深入。另外，节省了很多准备presentation用的ppt或者pdf所花费的时间，这些时间可以用来对问题作更深入的思考，获益要大得多。至于向Eric汇报的时候，甚至连白板都没有，每次都是完全依靠口述向他说明自己过去两个月的新进展以及下一步的计划，这挑战就更大了。这一年多下来，我不敢说口语有了多少进步，但是，在没有预先准备的情况下和导师长时间讨论学术问题或者向来访客人介绍自己的工作时，确实没有任何障碍了。

我觉得，要想最大限度地获得导师的认同和支持，最有效的方式莫过于经常和导师沟通，让他理解你的想法。

Postedby dahuasky  |  04月 20, 2009

什么时候能放慢脚步呢

一周前还憧憬一个悠闲的假期，不过这种卑微的愿望还是被现实击碎了，因为在接下来的这个星期，给我们funding的sponsors将会来访，在当前的形势下，这些人是最关键的。而且，由于ICCV而落下的一些课程内容也得花时间整理。只好在实验室度过“假期”了。原定的耶鲁之旅只好推迟了，在这里向欢子说声对不起了。

刚才查看邮箱时，发现在mit的工作邮箱里面的邮件突破10000份了~~这是一个值得纪念的日子。一眨眼，在这个校园里已经生活了很长时间了，这两年匆匆而过，甚至还来不及回味。

生活就像一壶普洱，囫囵而下终究索然无味，而细细品味方能体察回甘。在追求越来越高的目标的过程中，脚步越走越快，错过了多少值得欣赏的风景。突然有一个愿望，希望能给我一个月，放下一切的研究和工作，远离城市，在一个宁静的湖面，驾一叶扁舟，静静地观赏落日晚霞。

可是，在前路漫漫，时不我待的紧迫感中，这样的心愿也如镜花水月般虚渺。执着需要恒心，而放下需要豁达。也许，我能做到前者，但是，却一直没有智慧去放下，哪怕是暂时的放下。夜已深，胡思乱想撰下此文，算是小歇吧，presentation还准备了不到一半。。。

Postedby dahuasky  |  03月 30, 2009 

三月杂记

一个月的繁忙之后终于等到了春假，虽然还有很多事情要做，不过还是先给自己放两天假吧。过去一个月发生了许多不大不小的事情，给生活带来了一点色彩。

夏季的旅程

二月底的时候，先后得到了Microsoft还有CVPR的消息，于是，夏天的旅程总算确定下来了。从6月初到8月底的三个月内，我将要到Microsoft Research, Redmond做summer intern。在阔别微软将近五年后，再一次回来了，只是地点从北京换到了西雅图——一个传说中很美丽的城市。在这几个月里面，希望能去看看加州的阳光，看看Stanford和Google，看看在那里的朋友们。

在6月下旬，将会去Miami参加CVPR。对于迈阿密的海滩还是慕名已久了，这次度假的机会要好好珍惜。而且，说起来已经有两年多没有去参加Vision的会议了。期待在开会期间和做vision的新老朋友们好好聚聚。

关于Research

Research有一些基本的结果了，于是又面临了新的选择，从基本的部分出发可以引申出很多的探索方向，从中选择一个方向看来不是一件简单的事情。

前些天和Alan开会发生了一件有趣的事情：在谈到其中一个方向时，他对那个问题怎么做下去也不是很清楚。不过，他说有一位教授肯定告诉我们有用的东西。Alan说：he knows nearly everything …… 第一次，听到Alan对一个学者有这么高的评价。当我正在好奇的时候，Alan看到他说的那位“高人”正在附近——一位走路很慢，留着白胡子的老教授。Alan过去和他说了几句话，过了两分钟后，那位老先生拿着一篇paper过来了——“这也许就是你们要的吧”。实在太佩服了！

我接过paper看了看title：Combinatorial Differential Topologyand Geometry （组合微分拓扑与几何）——一种我之前从未听说的数学。  在我的知识中，组合研究的是离散的东西，而拓扑与几何研究的是连续空间的分析，不知道它们是如何结合的。不过，要是真的能成功结合起来，这样的数学工具也许对于我们面临的问题是最适合的了。

开完会后，我查了一下这位白胡子教授的资料：SanjoyK. Mitter。LIDS的前任Director，30年前当选IEEE Fellow，20年前当选美国工程院院士，2007年获得控制领域最高的终身成就奖Richard Bellman ControlHeritage Award。（做Vision的可能对Mitter教授不太熟悉，不过对于这个奖的另外一位获奖者Kalman，很多人都应该知晓）

更换系统

接触电脑这么长时间，现在对于新软件已经没有昔日那种热情了。但是，对于操作系统的换代还是充满好奇。在过去一个月里，正好赶上两个大系统的新版发布，于是把实验室的工作站，和家里的电脑的系统都换了。

在实验室，把Debian Linux从Etch (4.0)升级到了Lenny (5.0)。外观上看没有什么改变(KDE 3.5.9 –> 3.5.10)。不过，很多重要的部件都更新到了很新的版本了：firefox (2.0.x –> 3.07)，gcc (4.1.2 –> 4.3.3)，python  (2.4 –> 2.5.2)。以前一直感觉Debian 4.0落后时代太多，但是由于它和CSAIL的内部网络结合得最好，也就一直凑合了。。

微软的Windows 7测试版也发布了，并且在IEEE的MSDN Account上可以获得，于是就在寝室里把Vista换为Win 7，尝尝鲜。这一版还是很不错的，虽然是测试版，但是表现得相当稳定，而且驱动更加齐全了（什么驱动都不用装，整个机器就工作在很好的状态，包括Webcam）。 任务栏也做得很人性化了。但是，总体来说，它比起上一版本Vista的改变不是特别大。

GSL

这是一个CSAIL专有的名词，但是和学术无关——全称：Graduate Student Lunch。每个学年，很多CSAIL学生都会参加这项传统活动。这些学生分成很多小组，每个小组轮流负责在其中一个星期的星期五中午为参加这个活动的其它同学做午餐（大概有100多人参加这个活动，每个星期一般会有七八十人出席）。由于CSAIL的学生来自世界各地，所以，一年下来，能吃到很多国家的风味。费用基本由CSAIL负责，当然了，每个星期的采购总额是有上限的，不过一般够用。

上星期，轮到咱们了，中国人当然做中国菜了。星期四晚上，从8点忙活到深夜两点半，终于把给上百人吃的菜做出来了。我们自己一边做一边偷吃~~嘿嘿，感觉自己做的还是不错的。当时，忘了拍几张pp，有点可惜了。只是买了太多的肉丸子——yaodong说是把超市的冷冻柜里的各种丸子扫荡了——估计吃完那顿午饭后，很多人之后几个星期不会再去吃肉丸了，哈哈

新的朋友

冬去春来之际，我有幸认识了几位新的朋友，谢谢他们分享了不同的生活历程。这段时间，很多朋友正在申请，或者准备毕业，这是一个充满艰难的时节，等待总是让人焦躁不安，不过，就像Boston的冬天一样，再漫长的冬天也将会过去，等待我们的仍将是一个充满希望的春天。

Postedby dahuasky  |  03月 22, 2009

运动的解释

今天提一个我思考了很长时间的问题——不过到现在也还在思考中。

这几幅图描述了一个过程，究竟这个过程里面发生了什么呢？这个问题很简单，但是却反映了computer vision的一个核心问题，对图像或者图像序列的解释。

对于这个简单的例子，一个问题是：球发生运动了么？

如果拿computer vision里面基本的算法（做tracking的，alignment的，或者optical flow的），基本都会得到这样的结论：这个球发生了转动，（有个白斑从右方转到了左方）

再看一个例子，

 

这几幅图描述了另外一个过程。表面上看，这里发生了这样的运动，中间的红色块向上移动了。

可是，真实的情况是：这上面这两个过程都没有发生通常意义的几何运动，在第一组图片中，是外界光源发生了变化；在第二组图片中，是下排的LED由红变白，上排的由白变红。

怎么样才能让我们的computer vision的模型获得切合实际情况的描述呢？显然，在缺乏预定约束的情况下，上面所述的“真实情况”并不是对这些被观察到的过程的唯一合理的解释。也就是说，要获得“正确”的解释，除了这些observation以外，我们需要额外的信息或者知识。

这就是机器学习里面常说的“先验模型”——这对于这个发展了几十年的领域来说，并不是一个新鲜的故事。可是，现在paper中五花八门的prior model是不是真能解决上面的这些问题呢？我们翻开paper看看就知道，大部分的prior其实基本是用于regularization或者增强smoothness，对于两种本质上截然不同而同样能对data解释得很好的模型，这样的prior model显然是缺乏区分能力的。

要解决上面的问题，我们需要对prior有一个重新的思考。

这里有两种思路，一种是先验设限，另一种是后验选择。前者，就是在进行建模前，基于专门的知识，对于可供选择的模型范围设定限制。后者，就是在开始时允许多种解释，之后几何专门的知识去挑选合适的一种。

很多learning方面的朋友可能会更关心后面一种思路，而我自己的研究题目和前面一种更为相关，主要是建立一种代数系统，能够有效地对非常广泛的视觉变换过程进行描述或者施加约束。在这个体系中，对于受到某种限制的变换，能把它表达为一个子代数结构。对于上面的两个例子，要获得“真实描述”，只要把解限制在某个预定的子群上。当然，任何的数学体系在应用中都不能取代对具体问题的分析。我的研究的目的，只是为各种先验知识的表达提供工具，就像Graphical Model只是为变量之间的dependency的表达提供工具一样，它自己本身并不直接解决问题。

无论是什么方法，prior是解决computer vision的根本问题时无法绕开的，这是弥补low levelimage processing和high level model的semantic gap的最为重要的方面。而现有的研究中，prior的作用并没有得到充分的发挥，对于prior如何formulate也是莫衷一是。

不知道各位朋友对于上面两个例子所引申的问题有什么看法呢？

Postedby dahuasky  |  02月 25, 2009

我的PhD生活

一直以来，我在这个blog上写的都是偏重学术的文章。这一期就换一下口味吧，在这里聊聊我日常的生活。

在外面的人看来，MIT这所理工科的殿堂，或多或少有一点神秘的色彩。网上流传着很多关于这个学校的故事，包括Hacker，超负荷的课业，还有各种怪才。这些东西确实真实地存在着，却不是这里校园生活的主流。对于研究生来说，这里的日常生活是相当单调的，这种平凡得乏善可陈的生活和他们特别强调创新的研究工作形成了一种有趣的对比。

PhD的生活方式在很大程度上会受到导师的指导风格的影响。在这里，你问100个不同的PhD，他们会告诉你100种不同的生活方式——但是有一点是共同的，大家的工作都很繁忙。还是说说我自己的吧。在读master的时候，我只需要每过相当长的时间向汤老师汇报一次就行了；而在这里，我必须与三位不同的指导者讨论我的研究。

首先是Eric Grimson，他是我的正式的supervisor。但是，他有另外一重身份——MIT EECS的head，由于管理方面的事务极为繁忙，他在学术界上已经不太活跃了。我一般每个学期会和他有一到两次meeting，对自己的工作做一般性的汇报并且听他的建议，时间不长，通常是30到40分钟。向他做的报告，必须非常简明扼要，再复杂的topic，必须在5分钟内说完，并且要把要点说清楚，这对我来说是一个不小的挑战。然后他会向提出一些问题，并且对以后的大方向提出一些建议。对我来说，我并不期待这个简短的交流过程对我具体的research有多大的帮助，最主要的是要获得他对我的研究方向的持续支持。

然后是John Fisher，这里的一位Principal Scientist，他是我直接work with的人。和他的接触是相当频繁的，每周会有一次reading group，还有一次一对一的research meeting。在research meeting上，我会很具体的和他讨论我的研究，包括很多细节上的东西。一般来说。他会有很多建议，但是，仅仅是建议，没有要求我必须这样做——事实上有起码50%的建议，会被我当场驳回。不过，这并不影响我和他之间良好的合作，我们都认为这些是正常学术讨论中很自然的事情。

还有就是Alan Willsky了，LIDS的co-director。他是一个非常渊博的学者，对非常多的学科（信号处理，控制论，统计学习，数学）都着广泛而深刻的了解。每个星期，他和与他有关的学生进行分组讨论，我在其中的一组。我的研究涉及的相当重要的部分——李代数和微分方程，正是他非常熟悉的领域。一方面，我能够从和他的讨论中学到很多东西，事实上，我研究过程中的很多进展都得益于他的启发。另外一方面，他对这个领域太熟悉了，要让这方面的工作得到他的欣赏，是非常困难的。

在这里进行的研究，和我在MSRA或者CUHK做的研究有一个很不一样的地方，我的导师们非常强调一个工作是不是具有开创性的学术价值，而一个算法在实际中work不work，虽然也很重要，但不是放在最核心的地位的。我和他们讨论的绝大部分时间都是理论和方法论上的探讨，至于算法怎么在实验中更好的performance，他们assume是学生自己在实验过程通过各种方式中达到，这些东西如果和理论核心没有特别关系就不会是讨论的主要议题了。这不代表MIT或者CSAIL的全部，不过在我所在的“小环境”里，理论倾向是非常明显的。

在这里，不会有特别的paper或者project的压力，研究是自然地推进的，受会议deadline的影响会有一些（deadline前，如果刚好有一项工作差不多成熟了，需要多花点时间整理成paper），但不是特别明显。研究的最终目标是形成一份有重要影响的PhD thesis，因此，我们不会特别围着CVPR/ICCV/ICML/NIPS之类的会议转。如果留心统计的话，MIT在这些会议上发的文章不会比一个普通的学校多，但是在这里所完成的工作的长远影响远大于一般的学校。

能来到这里的学生，多多少少都希望能在学术上有自己的价值，而不仅仅是毕业后有一份还说得过去的工作——如果仅仅为了这点，用不着来这里，花那么长的时间（在我身边的同学里，5年甚至更长的很普遍的）读一个PhD。不过，现实中总是有着很多的压力和诱惑一点一点地消磨着学术上的理想。一方面，不是在paper-driven的氛围中工作，publication list的增长变得不那么迅速和激动人心；而对于高impact的研究的追求则时常会陷入挫折，推进缓慢。另一方面，faculty的opening逐渐减少和竞争日趋激烈，让前景变得不再是那么明朗。

与之相对比的是来自学术界以外的诱惑，比如工业界，华尔街，和管理咨询公司，它们一直以来都相当青睐从这里出去的学生（无论何种专业），而且有着极富竞争力的待遇。MIT统计了去年的top 5 employer: McKinsey, MIT,Google, Booz Allen, 和Boston Consulting Group，其中三家是顶尖的咨询公司；此外，虽然现在处在金融危机的时代，Morgan Stanley等的著名金融公司的校园招聘还在如常进行，仍旧吸引着很多的学生——而这个学校的学生里面，真正读管理和金融的是比例很小的——这说明了，很多理工科专业的同学去做consultant或者trader了。

这是一种令人困惑或者迷惘的对比。一部分人一直坚持自己的学术理想并取得成功（按照去年的统一，MIT的博士毕业生进入Education的占30%，我相信这里面大部分人并不是去教中学或者小学:-) ），而另外一部分人走进了商业的世界。这没有谁好谁不好的比较，每一次的人生选择都是一种choice——没有标准答案的choice。但是，一旦做出了选择，就意味着你在享受这种选择带给你的一切好的东西的同时，也必须承担所伴随的责任。

直到今天，我依然很执着地认为我会选择学术的道路，这是我内心中觉得最有价值的事情。如果到华尔街去，在为自己创造了财富的同时给世界上的其他人留下了什么——我想今天的局势或多或少表明了这个问题的答案。如果在科学上做出了真正的贡献，那么将给这个世界（至少是所工作的领域）带来进步和改变。一个人一生的价值，不在于他拥有了什么，而在于他创造了什么。

Postedby dahuasky  |  02月 21, 2009

千里积于跬步——流，向量场，和微分方程

在很多不同的科学领域里面，对于运动或者变化的描述和建模，都具有非常根本性的地位——我个人认为，在计算机视觉里面，这也是非常重要的。

什么是“流”？

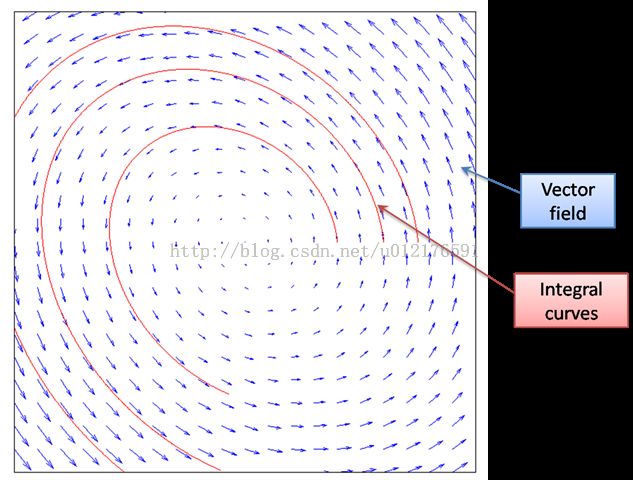
在我接触过的各种数学体系中，对于运动和变化的描述，我感觉最为适合的有两种不同的perspective：流和变换群。前者以被作用的对象为中心，运动就是这个东西随时间变化的函数；后者以变换本身为中心，研究的是各种变换所组成的空间的代数和拓扑结构。我想，相对来说，前者对于多数人而言似乎更为直观。在这篇文章里，就以“流”(Flow)的角度展开了。其实，这两种思路有着根本的联系——这种联系体现在李群论的一个基础概念——李群作用(Lie Group Action)，以及由它所延伸出来的丰富的理论。

流(Flow)是什么呢？很通俗的说，表示了一种运动规则。给定一个点的初始位置 x，让它运动一段时间 t，那么之后到达另一个位置 y，那么 y 就是初始位置 x 和运动时间 t 的函数：

y = S( t, x )

这个函数 S，如果符合一些合理的性质，就叫做一个流(Flow)。学过微分几何的同学可能会觉得这个定义与数学中的严格定义有点差距——确实如此。在微分几何中，流的概念需要建立在流形和单参数子群或者积分曲线的基础上，在一篇Blog文章中很难按照这样的方式阐述。只好在一定程度上放弃严密性，从直观出发，希望能传递出最基本的思想。

我们想想， 一个合理的运动函数应该具有什么性质呢？我想，最起码应该有三点：

1. 运动是连续的。物理学告诉我们，现实中没有所谓的“瞬间转移”。在上面的式子中，如果固定 x，那么 y( t ) = S(t, x) 就是这个初始位置在 x 的点的运动过程。在数学上，没有“瞬间转移”就是说对于任何 x，它的运动过程 y( t ) 都是连续的。
2. 变形是连续的。现在假设我们不考虑一个点，而是考虑一个物体。那么，本来是邻居的点，后来还是邻居——严格一点，在拓扑学上就是说，x 和它的一个邻域各自都运动了时间 t，那么运动后，这个邻域关系还是保持的——这等价于不改变这个物体的拓扑结构（比如，不把它撕开，但是连续变形是肯定允许的）。当然，在现实中物体被撕开不是没有可能，但是这会导致拓扑结构的改变，这就不是一般的数学工具所用表达的了。
3. 时间上的一致性。简单的说，如果我先让它运动时间 t1，在运动时间 t2，那么和让它运动时间 (t1 + t2)是一样的。用上面这个表达式写，就是：S( t2,  S( t1, x) ) = S(t2 + t1, x)。这个性质在物理上似乎理所当然，但是在数学上，你随便给一个二元函数S，可就未必符合这个属性了。这个规定保证了，我们定义出来的 S 最起码在物理上不会出现错乱。但是，它的意义不止于此，后面我们会看到，它在代数上，表示了一个群同构映射(Group homomorphism)——这种映射在李代数中有着核心作用。

总结起来，S(x, t) 是对于 x 和 t 的连续函数（实际上，在一般的定义中更严格一些，通常要求 S 是光滑函数，就是无限阶可微的函数。光滑性其实不是很强的条件，我们学过的全部初等函数都是光滑的）。还有就是关于时间的一致性条件。这里特别强调一点，我们允许 t 是可正可负的：时间取负数，就是让这个点沿着原路径倒回去走——怎么来的，就怎么回去。这里面隐含了一个条件：在某一时刻分开的两点是永远走不到一起成为一点的——否则倒回去就不知道往哪走了——这拓扑上，拓扑结构不发生改变就保证了这一点：物体既不能撕开，也不能粘在一起。

 

流——变换群和运动曲线的统一

这个S(t, x)呢，可以从两个方面去看，就得到两种不同的理解。首先，固定 t，

T_t ( x ) = S(t, x)

它就变成了一个关于x的变换函数：把一个点从一个位置变换到时间 t 后的另外一个位置。那么 T_t 就是一个变换。然后，不同的时间 t，对应着一个不同的变换。而且基于时间的一致性，先做 T_(t1) 变换（走时间 t1），再做 T_(t2) 变换（再走时间 t2），相当于另一个变换 T_(t2 + t1)。数学上就是：T_(t2) * T_(t1) = T_(t2 + t1)。如果你对群的概念有基本的了解，这里就可以看出来，从全部的不同时间的T_t 构成了一个变换群，从 t 到T_t 的映射，就是从实数R上的加法群到这个变换群的同构映射。因为 T_t 是由一个参数 t 控制的，有个专门的名词，叫做“单参数群”(one-parameter group)。由于加法群的可交换性，这个单参数变换群也是可交换的——这个可交换性的物理意义很明显: 先走t1，再走t2；还是先走t2，再走t1，是一样的。

因此，我们得到了第一种理解：流，就是连续作用在一个物体上的可交换单参数变换群。（这里所谓“物体”，在数学上有专门的名字“流形”，对于这点我不想展开太多了。）其实，这才是关于流的比较正规的定义。

从另外一个角度上看，固定 x，我们追踪这一个点的运动，

y_x ( t ) = S(t, x)

那么 y_x 就是初始位置（t=0时的位置）为 x 的点的运动过程——也叫做运动曲线(curve) 或者运动轨迹(orbit)。每个点都有自己的运动曲线，所谓流，就是这所有的这些运动曲线的共同体，或者说，流就是由这些运动曲线刻画的——这和我们一些直观的想法是一样的——我们在画画时喜欢在河上画几条曲线来表示流动。

这个函数S(t, x)，把变换群和运动曲线同一起来了——它们就是一个东西的两个不同侧面。到这里，我们向我们的目标迈出了第一步——最终，我们是要把变换群和向量场联系在一起——这就是李群和李代数的核心所在。

 

流与向量场

继续我们的故事。现在，我们有了y_x( t )，那么对它求导，我们就可以得到这个点在各个时刻的速度。整个流行就是所有这些曲线的集合，这样，在流形上的每个点，我们都能找到经过它的一条曲线，从而标出这点的速度。（这里强调一点，对于一个给定的流，经过某点的曲线是唯一的，你可以想想为什么？）于是，我们给每个点都赋予了一个速度，这就是“速度场”(velocity field)。每个速度就是曲线上的一个切向量，所以更一般的说，我们把它叫做“向量场”。这里，我们看到，任意一个流都可以通过运动曲线的速度来建立一个对应的向量场。而且可以证明，这个向量场是连续的。

那么反过来呢？我们给定一个连续的向量场，能不能找到一个流和它对应呢？这里面有三个方面

1. （存在性），能不能找到一个流，它的速度场等于给定的向量场。
2. （唯一性），如果存在，这个流是不是唯一的。
3. （连续性），这个流 S(t, x) 是不是关于 x 和 t 的连续函数（或者光滑函数）。

这个问题是一个很深刻的问题，它的回答直接联系到一般意义的常微分方程的解的存在性，唯一性，和连续性。答案是，这在局部上是成立的。就是任意一个定义于流形上的向量场，对于流形上的任何一点，总能找到包含它的一个“局部流形”（开子流形），以及定义在这个局部上的流，使得流的速度场和给定的向量场在这个局部相等。简洁一点说，符合条件的流在处处“局部存在”。而且，它们在某种意义上是唯一的，就是两个符合条件的“局部流”，它们在定义域重合的部分是相等的。如果给定向量场是连续（光滑）的话，那么导出的流也是连续（光滑）的。

我不打算给出严格的证明，这可以在很多微分流形的相关资料中找到。这里，我希望用一个通俗的过程来介绍，怎么构造出这个流。我们把向量场看成是在一个大地图上标了很多很密的指示牌——告诉你到了这点后应该用多大的速度往什么方向开车。于是，你从某个地方出发，你先看看附近的指示牌，把车子调整到指示的速度和方向，往前开一小段后看到下一个指示，继续调整速度和方向，一直这样下去，你开车的过程就形成了一个运动轨迹，而且在各点上的速度，都和该点的指示一致。设想一个极限过程，指示牌无限密集，开车的人每个时刻都在连续地调节速度，那么就得到了一个和向量场一致的运动曲线。我们上面说过，流是所有这些运动曲线的集体，于是我们从不同的地方开始开车，最后就能把整个流构造出来了。

有些时候，向量场的定义域可能不是很完整，那么车子不能无限开下去（不然可能开出去了），这时候只能给出“局部的流”。如果一个向量场存在一个全局的流，就叫做完备的向量场(Complete Vector Field)。

从这个故事，我们知道一个变换是怎么炼成的：就是按照指示，一步步的做，这些小步积累起来，就形成最后的变换效果。有什么样的指示，就会有什么样的变换。在李群论中，数学家给向量场起了个名字：infinitestimal generator——寓意是，千里变换，生于跬步。数学上，“千里”与“跬步”的关系，就是李群和李代数的联系。

为什么我们不直接描述变换，而言描述生成它的向量场呢？很简单，很多时候全局的演化不容易直接描述，而小步的前进则是很容易把握的。在很多问题中，我们知道“divide and conquer“的策略能够大大简化问题，从变换群到向量场正是这种策略的极限体现。一个简单的例子，比如我们要表示一个不会改变物体大小的变换过程，所谓“不可压缩性”如果用变换矩阵直接表达，那是一个颇为复杂的非线性约束，而如果使用向量场表达，我们只需要把向量场限制在某个有限维子空间里——这就是一个简单得多的线性约束。这样的例子还有很多很多。

 

和微分方程的联系

最后，我们再回头看看上面这个“从向量场推导流”的问题。我们知道所谓速度场，就是对 t的导数，所以这个问题，可以写成：

给定向量场 V(x)， 求 S(t, x) 使得 d S(t, x) / dt = V(x)， 并且 S(0, x) = x

这就是一般意义的常微分方程的初值问题。对这个问题的回答，和对于常微分方程的解得存在性，唯一性和连续性的回答，是联系在一起的。给定一个向量场，就相当于给出一个常微分方程。如果给定 x,那么所形成的曲线 y_x ( t )，就是上述微分方程的解，而流 S(t, x) 就是所有这些解的整体。我们知道微分方程的解通常以积分形式给出，所以上面说的“运动曲线”，在数学上有个正式的学名叫“积分曲线”(Integral curve)。

在物理上，“积分曲线”也是很容易理解的，就是把“速度指示牌”的指示积累起来形成的路径，积分曲线生成的过程就是“积跬步而致千里”的过程。而且，这不仅仅是一种形象思考，在实际问题中微分方程的数值解法正好就是这种过程的最好体现。

Postedby dahuasky  |  02月 8, 2009

在数学的海洋中飘荡

在过去的一年中，我一直在数学的海洋中游荡，research进展不多，对于数学世界的阅历算是有了一些长进。

为什么要深入数学的世界

作为计算机的学生，我没有任何企图要成为一个数学家。我学习数学的目的，是要想爬上巨人的肩膀，希望站在更高的高度，能把我自己研究的东西看得更深广一些。说起来，我在刚来这个学校的时候，并没有预料到我将会有一个深入数学的旅程。我的导师最初希望我去做的题目，是对appearance和motion建立一个unified的model。这个题目在当今Computer Vision中百花齐放的世界中并没有任何特别的地方。事实上，使用各种GraphicalModel把各种东西联合在一起framework，在近年的论文中并不少见。

我不否认现在广泛流行的Graphical Model是对复杂现象建模的有力工具，但是，我认为它不是panacea，并不能取代对于所研究的问题的深入的钻研。如果统计学习包治百病，那么很多“下游”的学科也就没有存在的必要了。事实上，开始的时候，我也是和Vision中很多人一样，想着去做一个Graphical Model——我的导师指出，这样的做法只是重复一些标准的流程，并没有很大的价值。经过很长时间的反复，另外一个路径慢慢被确立下来——我们相信，一个图像是通过大量“原子”的某种空间分布构成的，原子群的运动形成了动态的可视过程。微观意义下的单个原子运动，和宏观意义下的整体分布的变换存在着深刻的联系——这需要我们去发掘。

在深入探索这个题目的过程中，遇到了很多很多的问题，如何描述一个一般的运动过程，如何建立一个稳定并且广泛适用的原子表达，如何刻画微观运动和宏观分布变换的联系，还有很多。在这个过程中，我发现了两个事情：

• 我原有的数学基础已经远远不能适应我对这些问题的深入研究。
• 在数学中，有很多思想和工具，是非常适合解决这些问题的，只是没有被很多的应用科学的研究者重视。

于是，我决心开始深入数学这个浩瀚大海，希望在我再次走出来的时候，我已经有了更强大的武器去面对这些问题的挑战。

我的游历并没有结束，我的视野相比于这个博大精深的世界的依旧显得非常狭窄。在这里，我只是说说，在我的眼中，数学如何一步步从初级向高级发展，更高级别的数学对于具体应用究竟有何好处。

 

集合论：现代数学的共同基础

现代数学有数不清的分支，但是，它们都有一个共同的基础——集合论——因为它，数学这个庞大的家族有个共同的语言。集合论中有一些最基本的概念：集合(set)，关系(relation)，函数(function)，等价(equivalence)，是在其它数学分支的语言中几乎必然存在的。对于这些简单概念的理解，是进一步学些别的数学的基础。我相信，理工科大学生对于这些都不会陌生。

不过，有一个很重要的东西就不见得那么家喻户晓了——那就是“选择公理”(Axiom of Choice)。这个公理的意思是“任意的一群非空集合，一定可以从每个集合中各拿出一个元素。”——似乎是显然得不能再显然的命题。不过，这个貌似平常的公理却能演绎出一些比较奇怪的结论，比如巴拿赫-塔斯基分球定理——“一个球，能分成五个部分，对它们进行一系列刚性变换（平移旋转）后，能组合成两个一样大小的球”。正因为这些完全有悖常识的结论，导致数学界曾经在相当长时间里对于是否接受它有着激烈争论。现在，主流数学家对于它应该是基本接受的，因为很多数学分支的重要定理都依赖于它。在我们后面要回说到的学科里面，下面的定理依赖于选择公理：

1. 拓扑学：Baire Category Theorem
2. 实分析（测度理论）：Lebesgue 不可测集的存在性
3. 泛函分析四个主要定理：Hahn-Banach Extension Theorem, Banach-Steinhaus Theorem (Uniform boundedness principle), Open Mapping Theorem, Closed Graph Theorem

在集合论的基础上，现代数学有两大家族：分析(Analysis)和代数(Algebra)。至于其它的，比如几何和概率论，在古典数学时代，它们是和代数并列的，但是它们的现代版本则基本是建立在分析或者代数的基础上，因此从现代意义说，它们和分析与代数并不是平行的关系。

 

分析：在极限基础上建立的宏伟大厦

微积分：分析的古典时代——从牛顿到柯西

先说说分析(Analysis)吧，它是从微积分(Caculus)发展起来的——这也是有些微积分教材名字叫“数学分析”的原因。不过，分析的范畴远不只是这些，我们在大学一年级学习的微积分只能算是对古典分析的入门。分析研究的对象很多，包括导数(derivatives)，积分(integral)，微分方程(differential equation)，还有级数(infiniteseries)——这些基本的概念，在初等的微积分里面都有介绍。如果说有一个思想贯穿其中，那就是极限——这是整个分析（不仅仅是微积分）的灵魂。

一个很多人都听说过的故事，就是牛顿(Newton)和莱布尼茨(Leibniz)关于微积分发明权的争论。事实上，在他们的时代，很多微积分的工具开始运用在科学和工程之中，但是，微积分的基础并没有真正建立。那个长时间一直解释不清楚的“无穷小量”的幽灵，困扰了数学界一百多年的时间——这就是“第二次数学危机”。直到柯西用数列极限的观点重新建立了微积分的基本概念，这门学科才开始有了一个比较坚实的基础。直到今天，整个分析的大厦还是建立在极限的基石之上。

柯西(Cauchy)为分析的发展提供了一种严密的语言，但是他并没有解决微积分的全部问题。在19世纪的时候，分析的世界仍然有着一些挥之不去的乌云。而其中最重要的一个没有解决的是“函数是否可积的问题”。我们在现在的微积分课本中学到的那种通过“无限分割区间，取矩阵面积和的极限”的积分，是大约在1850年由黎曼(Riemann)提出的，叫做黎曼积分。但是，什么函数存在黎曼积分呢（黎曼可积）？数学家们很早就证明了，定义在闭区间内的连续函数是黎曼可积的。可是，这样的结果并不令人满意，工程师们需要对分段连续函数的函数积分。

实分析：在实数理论和测度理论上建立起现代分析

在19世纪中后期，不连续函数的可积性问题一直是分析的重要课题。对于定义在闭区间上的黎曼积分的研究发现，可积性的关键在于“不连续的点足够少”。只有有限处不连续的函数是可积的，可是很多有数学家们构造出很多在无限处不连续的可积函数。显然，在衡量点集大小的时候，有限和无限并不是一种合适的标准。在探讨“点集大小”这个问题的过程中，数学家发现实数轴——这个他们曾经以为已经充分理解的东西——有着许多他们没有想到的特性。在极限思想的支持下，实数理论在这个时候被建立起来，它的标志是对实数完备性进行刻画的几条等价的定理（确界定理，区间套定理，柯西收敛定理，Bolzano-Weierstrass Theorem和Heine-BorelTheorem等等）——这些定理明确表达出实数和有理数的根本区别：完备性（很不严格的说，就是对极限运算封闭）。随着对实数认识的深入，如何测量“点集大小”的问题也取得了突破，勒贝格创造性地把关于集合的代数，和Outer content（就是“外测度”的一个雏形）的概念结合起来，建立了测度理论(MeasureTheory)，并且进一步建立了以测度为基础的积分——勒贝格(Lebesgue Integral)。在这个新的积分概念的支持下，可积性问题变得一目了然。

上面说到的实数理论，测度理论和勒贝格积分，构成了我们现在称为实分析(Real Analysis)的数学分支，有些书也叫实变函数论。对于应用科学来说，实分析似乎没有古典微积分那么“实用”——很难直接基于它得到什么算法。而且，它要解决的某些“难题”——比如处处不连续的函数，或者处处连续而处处不可微的函数——在工程师的眼中，并不现实。但是，我认为，它并不是一种纯数学概念游戏，它的现实意义在于为许多现代的应用数学分支提供坚实的基础。下面，我仅仅列举几条它的用处：

1. 黎曼可积的函数空间不是完备的，但是勒贝格可积的函数空间是完备的。简单的说，一个黎曼可积的函数列收敛到的那个函数不一定是黎曼可积的，但是勒贝格可积的函数列必定收敛到一个勒贝格可积的函数。在泛函分析，还有逼近理论中，经常需要讨论“函数的极限”，或者“函数的级数”，如果用黎曼积分的概念，这种讨论几乎不可想像。我们有时看一些paper中提到Lp函数空间，就是基于勒贝格积分。
2. 勒贝格积分是傅立叶变换（这东西在工程中到处都是）的基础。很多关于信号处理的初等教材，可能绕过了勒贝格积分，直接讲点面对实用的东西而不谈它的数学基础，但是，对于深层次的研究问题——特别是希望在理论中能做一些工作——这并不是总能绕过去。
3. 在下面，我们还会看到，测度理论是现代概率论的基础。

拓扑学：分析从实数轴推广到一般空间——现代分析的抽象基础

随着实数理论的建立，大家开始把极限和连续推广到更一般的地方的分析。事实上，很多基于实数的概念和定理并不是实数特有的。很多特性可以抽象出来，推广到更一般的空间里面。对于实数轴的推广，促成了点集拓扑学(Point-set Topology)的建立。很多原来只存在于实数中的概念，被提取出来，进行一般性的讨论。在拓扑学里面，有4个C构成了它的核心：

1. Closed set（闭集合）。在现代的拓扑学的公理化体系中，开集和闭集是最基本的概念。一切从此引申。这两个概念是开区间和闭区间的推广，它们的根本地位，并不是一开始就被认识到的。经过相当长的时间，人们才认识到：开集的概念是连续性的基础，而闭集对极限运算封闭——而极限正是分析的根基。
2. Continuous function （连续函数）。连续函数在微积分里面有个用epsilon-delta语言给出的定义，在拓扑学中它的定义是“开集的原像是开集的函数”。第二个定义和第一个是等价的，只是用更抽象的语言进行了改写。我个人认为，它的第三个（等价）定义才从根本上揭示连续函数的本质——“连续函数是保持极限运算的函数”——比如y是数列x1, x2, x3, … 的极限， 那么如果 f 是连续函数，那么 f(y) 就是 f(x1), f(x2), f(x3), …的极限。连续函数的重要性，可以从别的分支学科中进行类比。比如群论中，基础的运算是“乘法”，对于群，最重要的映射叫“同态映射”——保持“乘法”的映射。在分析中，基础运算是“极限”，因此连续函数在分析中的地位，和同态映射在代数中的地位是相当的。
3. Connected set （连通集合）。比它略为窄一点的概念叫(Path connected)，就是集合中任意两点都存在连续路径相连——可能是一般人理解的概念。一般意义下的连通概念稍微抽象一些。在我看来，连通性有两个重要的用场：一个是用于证明一般的中值定理(Intermediate Value Theorem)，还有就是代数拓扑，拓扑群论和李群论中讨论根本群(Fundamental Group)的阶。
4. Compact set（紧集）。Compactness似乎在初等微积分里面没有专门出现，不过有几条实数上的定理和它其实是有关系的。比如，“有界数列必然存在收敛子列”——用compactness的语言来说就是——“实数空间中有界闭集是紧的”。它在拓扑学中的一般定义是一个听上去比较抽象的东西——“紧集的任意开覆盖存在有限子覆盖”。这个定义在讨论拓扑学的定理时很方便，它在很多时候能帮助实现从无限到有限的转换。对于分析来说，用得更多的是它的另一种形式——“紧集中的数列必存在收敛子列”——它体现了分析中最重要的“极限”。Compactness在现代分析中运用极广，无法尽述。微积分中的两个重要定理：极值定理(Extreme Value Theory)，和一致收敛定理(Uniform Convergence Theorem)就可以借助它推广到一般的形式。

从某种意义上说，点集拓扑学可以看成是关于“极限”的一般理论，它抽象于实数理论，它的概念成为几乎所有现代分析学科的通用语言，也是整个现代分析的根基所在。

微分几何：流形上的分析——在拓扑空间上引入微分结构

拓扑学把极限的概念推广到一般的拓扑空间，但这不是故事的结束，而仅仅是开始。在微积分里面，极限之后我们有微分，求导，积分。这些东西也可以推广到拓扑空间，在拓扑学的基础上建立起来——这就是微分几何。从教学上说，微分几何的教材，有两种不同的类型，一种是建立在古典微机分的基础上的“古典微分几何”，主要是关于二维和三维空间中的一些几何量的计算，比如曲率。还有一种是建立在现代拓扑学的基础上，这里姑且称为“现代微分几何”——它的核心概念就是“流形”(manifold)——就是在拓扑空间的基础上加了一套可以进行微分运算的结构。现代微分几何是一门非常丰富的学科。比如一般流形上的微分的定义就比传统的微分丰富，我自己就见过三种从不同角度给出的等价定义——这一方面让事情变得复杂一些，但是另外一个方面它给了同一个概念的不同理解，往往在解决问题时会引出不同的思路。除了推广微积分的概念以外，还引入了很多新概念：tangent space, cotangent space, push forward, pull back, fibrebundle, flow, immersion, submersion 等等。

近些年，流形在machine learning似乎相当时髦。但是，坦率地说，要弄懂一些基本的流形算法，甚至“创造”一些流形算法，并不需要多少微分几何的基础。对我的研究来说，微分几何最重要的应用就是建立在它之上的另外一个分支：李群和李代数——这是数学中两大家族分析和代数的一个漂亮的联姻。分析和代数的另外一处重要的结合则是泛函分析，以及在其基础上的调和分析。

 

代数：一个抽象的世界

关于抽象代数

回过头来，再说说另一个大家族——代数。

如果说古典微积分是分析的入门，那么现代代数的入门点则是两个部分：线性代数(linear algebra)和基础的抽象代数(abstract algebra)——据说国内一些教材称之为近世代数。

代数——名称上研究的似乎是数，在我看来，主要研究的是运算规则。一门代数，其实都是从某种具体的运算体系中抽象出一些基本规则，建立一个公理体系，然后在这基础上进行研究。一个集合再加上一套运算规则，就构成一个代数结构。在主要的代数结构中，最简单的是群(Group)——它只有一种符合结合率的可逆运算，通常叫“乘法”。如果，这种运算也符合交换率，那么就叫阿贝尔群(Abelian Group)。如果有两种运算，一种叫加法，满足交换率和结合率，一种叫乘法，满足结合率，它们之间满足分配率，这种丰富一点的结构叫做环(Ring)，如果环上的乘法满足交换率，就叫可交换环(Commutative Ring)。如果，一个环的加法和乘法具有了所有的良好性质，那么就成为一个域(Field)。基于域，我们可以建立一种新的结构，能进行加法和数乘，就构成了线性代数(Linearalgebra)。

代数的好处在于，它只关心运算规则的演绎，而不管参与运算的对象。只要定义恰当，完全可以让一只猫乘一只狗得到一头猪:-)。基于抽象运算规则得到的所有定理完全可以运用于上面说的猫狗乘法。当然，在实际运用中，我们还是希望用它干点有意义的事情。学过抽象代数的都知道，基于几条最简单的规则，比如结合律，就能导出非常多的重要结论——这些结论可以应用到一切满足这些简单规则的地方——这是代数的威力所在，我们不再需要为每一个具体领域重新建立这么多的定理。

抽象代数有在一些基础定理的基础上，进一步的研究往往分为两个流派：研究有限的离散代数结构（比如有限群和有限域），这部分内容通常用于数论，编码，和整数方程这些地方；另外一个流派是研究连续的代数结构，通常和拓扑与分析联系在一起（比如拓扑群，李群）。我在学习中的focus主要是后者。

线性代数：“线性”的基础地位

对于做Learning, vision,optimization或者statistics的人来说，接触最多的莫过于线性代数——这也是我们在大学低年级就开始学习的。线性代数，包括建立在它基础上的各种学科，最核心的两个概念是向量空间和线性变换。线性变换在线性代数中的地位，和连续函数在分析中的地位，或者同态映射在群论中的地位是一样的——它是保持基础运算（加法和数乘）的映射。

在learning中有这样的一种倾向——鄙视线性算法，标榜非线性。也许在很多场合下面，我们需要非线性来描述复杂的现实世界，但是无论什么时候，线性都是具有根本地位的。没有线性的基础，就不可能存在所谓的非线性推广。我们常用的非线性化的方法包括流形和kernelization，这两者都需要在某个阶段回归线性。流形需要在每个局部建立和线性空间的映射，通过把许多局部线性空间连接起来形成非线性；而kernerlization则是通过置换内积结构把原线性空间“非线性”地映射到另外一个线性空间，再进行线性空间中所能进行的操作。而在分析领域，线性的运算更是无处不在，微分，积分，傅立叶变换，拉普拉斯变换，还有统计中的均值，通通都是线性的。

泛函分析：从有限维向无限维迈进

在大学中学习的线性代数，它的简单主要因为它是在有限维空间进行的，因为有限，我们无须借助于太多的分析手段。但是，有限维空间并不能有效地表达我们的世界——最重要的，函数构成了线性空间，可是它是无限维的。对函数进行的最重要的运算都在无限维空间进行，比如傅立叶变换和小波分析。这表明了，为了研究函数（或者说连续信号），我们需要打破有限维空间的束缚，走入无限维的函数空间——这里面的第一步，就是泛函分析。

泛函分析(Functional Analysis)是研究的是一般的线性空间，包括有限维和无限维，但是很多东西在有限维下显得很trivial，真正的困难往往在无限维的时候出现。在泛函分析中，空间中的元素还是叫向量，但是线性变换通常会叫作“算子”(operator)。除了加法和数乘，这里进一步加入了一些运算，比如加入范数去表达“向量的长度”或者“元素的距离”，这样的空间叫做“赋范线性空间”(normed space)，再进一步的，可以加入内积运算，这样的空间叫“内积空间”(Innerproduct space)。

大家发现，当进入无限维的时间时，很多老的观念不再适用了，一切都需要重新审视。

1. 所有的有限维空间都是完备的（柯西序列收敛），很多无限维空间却是不完备的（比如闭区间上的连续函数）。在这里，完备的空间有特殊的名称：完备的赋范空间叫巴拿赫空间(Banach space)，完备的内积空间叫希尔伯特空间(Hilbert space)。
2. 在有限维空间中空间和它的对偶空间的是完全同构的，而在无限维空间中，它们存在微妙的差别。
3. 在有限维空间中，所有线性变换（矩阵）都是有界变换，而在无限维，很多算子是无界的(unbounded)，最重要的一个例子是给函数求导。
4. 在有限维空间中，一切有界闭集都是紧的，比如单位球。而在所有的无限维空间中，单位球都不是紧的——也就是说，可以在单位球内撒入无限个点，而不出现一个极限点。
5. 在有限维空间中，线性变换（矩阵）的谱相当于全部的特征值，在无限维空间中，算子的谱的结构比这个复杂得多，除了特征值组成的点谱(point spectrum)，还有approximate point spectrum和residual spectrum。虽然复杂，但是，也更为有趣。由此形成了一个相当丰富的分支——算子谱论(Spectrum theory)。
6. 在有限维空间中，任何一点对任何一个子空间总存在投影，而在无限维空间中，这就不一定了，具有这种良好特性的子空间有个专门的名称切比雪夫空间(Chebyshev space)。这个概念是现代逼近理论的基础(approximation theory)。函数空间的逼近理论在Learning中应该有着非常重要的作用，但是现在看到的运用现代逼近理论的文章并不多。

继续往前：巴拿赫代数，调和分析，和李代数

基本的泛函分析继续往前走，有两个重要的方向。第一个是巴拿赫代数(Banach Algebra)，它就是在巴拿赫空间（完备的内积空间）的基础上引入乘法（这不同于数乘）。比如矩阵——它除了加法和数乘，还能做乘法——这就构成了一个巴拿赫代数。除此以外，值域完备的有界算子，平方可积函数，都能构成巴拿赫代数。巴拿赫代数是泛函分析的抽象，很多对于有界算子导出的结论，还有算子谱论中的许多定理，它们不仅仅对算子适用，它们其实可以从一般的巴拿赫代数中得到，并且应用在算子以外的地方。巴拿赫代数让你站在更高的高度看待泛函分析中的结论，但是，我对它在实际问题中能比泛函分析能多带来什么东西还有待思考。

最能把泛函分析和实际问题在一起的另一个重要方向是调和分析(HarmonicAnalysis)。我在这里列举它的两个个子领域，傅立叶分析和小波分析，我想这已经能说明它的实际价值。它研究的最核心的问题就是怎么用基函数去逼近和构造一个函数。它研究的是函数空间的问题，不可避免的必须以泛函分析为基础。除了傅立叶和小波，调和分析还研究一些很有用的函数空间，比如Hardy space，Sobolev space，这些空间有很多很好的性质，在工程中和物理学中都有很重要的应用。对于vision来说，调和分析在信号的表达，图像的构造，都是非常有用的工具。

当分析和线性代数走在一起，产生了泛函分析和调和分析；当分析和群论走在一起，我们就有了李群(Lie Group)和李代数(Lie Algebra)。它们给连续群上的元素赋予了代数结构。我一直认为这是一门非常漂亮的数学：在一个体系中，拓扑，微分和代数走到了一起。在一定条件下，通过李群和李代数的联系，它让几何变换的结合变成了线性运算，让子群化为线性子空间，这样就为Learning中许多重要的模型和算法的引入到对几何运动的建模创造了必要的条件。因此，我们相信李群和李代数对于vision有着重要意义，只不过学习它的道路可能会很艰辛，在它之前需要学习很多别的数学。

 

现代概率论：在现代分析基础上再生　

最后，再简单说说很多Learning的研究者特别关心的数学分支：概率论。自从Kolmogorov在上世纪30年代把测度引入概率论以来，测度理论就成为现代概率论的基础。在这里，概率定义为测度，随机变量定义为可测函数，条件随机变量定义为可测函数在某个函数空间的投影，均值则是可测函数对于概率测度的积分。值得注意的是，很多的现代观点，开始以泛函分析的思路看待概率论的基础概念，随机变量构成了一个向量空间，而带符号概率测度则构成了它的对偶空间，其中一方施加于对方就形成均值。角度虽然不一样，不过这两种方式殊途同归，形成的基础是等价的。

在现代概率论的基础上，许多传统的分支得到了极大丰富，最有代表性的包括鞅论(Martingale)——由研究赌博引发的理论，现在主要用于金融（这里可以看出赌博和金融的理论联系，:-P），布朗运动(Brownian Motion)——连续随机过程的基础，以及在此基础上建立的随机分析(Stochastic Calculus)，包括随机积分（对随机过程的路径进行积分，其中比较有代表性的叫伊藤积分(Ito Integral)），和随机微分方程。对于连续几何运用建立概率模型以及对分布的变换的研究离不开这些方面的知识。

 

终于写完了——也谢谢你把这么长的文章看完，希望其中的一些内容对你是有帮助的。

Postedby dahuasky  |  01月 22, 2009 

飞雪中迎来2009

在漫天大雪中，Boston走进了2009年。

我们生活的星球，在过去的一年经历了太多的不平凡。我从来没有想象过，我会在这短短一年中，和所有人一起见证了这个世界的跌宕起伏。

如果说2007年是我人生的转折，那么，我在2008年的生活则又重新回到了平淡。和校园外的惊心动魄相比，在校园内发生的一切显得如此的波澜不惊，甚至乏善可陈。

身边的同学大都回国了，一个人在异国他乡的风雪中迎接新年的时候，感受到了一种不一样的滋味。一个人的时候，有时候会感到孤寂，或者迷惘，这也许是留学生都必须经受的考验。人的一生并不漫长，几年的学习生活，如果在无所事事的享乐中虚度，无论从哪个意义上说都是对自己生命的巨大浪费。感谢朋友们每次在我感到迷惘的时候，提醒我回到我前进的轨道上来。来到这里学习的目的，不是为了美国的花花世界，也不是为了一纸PhD文凭，而是为在未来能创造自己的真正的价值。MIT这几个字母，与其说是一个光环，不如说是一种压力——它在给你提供了更好的学习条件的同时，也剥夺了你失败的借口——如果这几年不能做出有价值的东西，那么，世界级学府的学位带来的只是耻辱，而不是荣耀。

我曾经以为，自己在香港时的基础已经足以支持我完成高水平的工作——实为无知者无畏。在探讨很多问题的时候，我发现我现在的能力离我自己的目标还有很大的距离。我越来越相信，扎实的根基是做出真正有价值的东西的最重要的保证。把自己的工作发表出来，需要presentation的能力；但是仅此本身，也许能带来paper，却不能带来真实的贡献。我们的世界不缺乏聪明人，用几天时间想出一些“novel idea”对于一个在学术界有一些日子的人来说不是特别困难的事情。相反，我们更缺乏的也许是静下心来提高自己，深入钻研的耐心和决心。

回顾过去一年，我做的最有价值的事情，莫过于把大量时间投入到现代数学的学习之中。通过对一系列涵盖代数，拓扑，概率，分析等主要领域的数学分支的学习，我感觉到了明显的收获。对于很多重要理论的核心思想有了更深切的把握，而不再停留于表层的肤浅理解。更重要的是，我明白了我的工作和那些学术上真正有生命力的工作相去有多远，我并没有资本到处吹嘘自己的idea多聪明，然后批评别人的工作是垃圾，对我来说，还有很多不懂的地方需要去学习。

我自己对于我PhD毕业的要求是：发现并真正解决一个有意义的问题。我相信这不是一个简单的挑战。对于未来的一年，我的期待是，通过继续学习，为这个目标的实现铺平道路。

至于在学术以外，我年复一年的把一个尚未实现的愿望带进新的一年，今年也不例外:-)。现实需要我们不断做出妥协，但是，在某些地方，尤其在心灵深处，我仍然在守护着那一点对完美的执著和对浪漫的希冀。生活需要一点追求，没有追求的生活也就没有了动力和价值。

最后，衷心祝愿每一位朋友在新的一年愿望成真。

Postedby dahuasky  |  01月 1, 2009

Merry Christmas

圣诞来得如此安宁。。。

 

祝愿朋友们圣诞快乐。

 

 

Postedby dahuasky  |  12月 25, 2008

Updated math book list

在右边的book list增加了一本新书：

 

Introduction to Hilbert Spaces  (byLokenath Debnath and Piotr Mikusinski)

 

这本书可以和一般的泛函分析教材是互补的。现在主流的关于functionalanalysis的textbook，虽然也会讲述内积(innerproduct)和希尔伯特空间(Hilbert Space)，但是，主要篇幅还是放在和范数理论和巴拿赫空间(Banach Space)相关的理论。而内积结构，双线性泛函，自伴算子的谱论，有时讲得不是特别充分。而这方面的知识在Learning和Signal Processing这些领域中往往比norm和Banach Space有更广泛的运用。它们通常在一些名字带有Hilbert Space的书中有更深入的探讨——有些作者把这部分理论称作“希尔伯特空间理论”，作为和“巴拿赫空间理论”平行的数学分支。前者主要关注内积，而后者更多关注范数。

 

上面提到的这本书，对于希尔伯特空间理论以及它的应用作了相当不错的介绍。在保证数学上严密的前提下，理论表述清晰，容易理解，而且篇章结构也比较合理。不需要太多的数学基础，只要求读者具备基本的微积分，微分方程，和线性代数的知识。

 

比较有意思的是它的第二章对于勒贝格积分(Lesbegue Integral)的介绍，一改传统的先讲测度理论为铺垫的做法，而是直接从阶梯函数和实数域的某些性质入手，绕开测度来讲。可能我以前对于测度和积分的关系的理解受传统教材影响比较深，一开始对这种讲授方式也不是很习惯。不过，反复思考，把这两种讲法结合起来，发现这种新的切入方式确实能提供一种有启发性的perspective。

 

这本书另外一个有特色的地方是，它的后半部分，讲述了Hilbert SpaceTheory在不同领域的应用，包括微分方程系统，量子力学，小波分析，和优化。基于希尔伯特空间和算子论的视角，对这些学科重新进行阐述。当然，它不可能取代这些学科本身的教材，但是，这种基于算子的解说，带来了一些很有意义的理解。

 

 

 

Postedby dahuasky  |  12月 14, 2008

永不消逝的浪漫：Programming Languages and Haskell

最近两周工作轻松了一些，于是闲不住，花了不少时间钻研一门新的程序设计语言——Haskell。其实，这门语言在上世纪八十年代就产生了，到现在也算有些年纪了吧，只是对我来说，是第一次学习它。

从初中学习Basic，到现在，学过的语言不记得有多少了，在相当一段时间内用来干serious的事情的应该也有八九种了。我这个人在对待计算机语言方面属于“喜新不厌旧”（在现实生活中，我还是很专一滴~~~）

先说说对几个老相好的印象吧：

不一样的她，不一样的魅力

Basic / Pascal：初中时代的初恋情人，历史有点久远。。。只是没事的时候时不时在脑海翻出和TurboPascal的蓝底白字共同度过的good old days来怀旧一把。

C / C++：从高中相识到现在，一直不离不弃，也是学习得最全面的一种语言，从Helloworld，到Boost/Loki里面的各种被称“奇技淫巧”的Templatetechnique都玩了个遍。OOP + Template的表达力，High performance，和对机器的直接控制能力的结合，成就了它在长达几十年历久不衰的生命力。在性能关键的地方，它是不二的选择。但是，选择它往往也意味选择承担它给你带来的痛苦：一版代码干不了几件正事，层不不穷的指针错误和内存溢出，编译复杂的模板类时几英里长的诡异错误。

软件工程的教科书说良好的设计可以帮助我们在很大程度上避免这些错误，这话一点不假。但是，这里面的根本问题是：我们花了太多的精力在这些地方——而它们并不是我们真正要做的事情。我本来想开车去玩的，但是，我却花了更多的时间去修路——为了让车子更安全顺畅。

C#：这门语言很年轻，我看着它从1.0成长到4.0。和它呆在一起很舒服，就像和一位充满青春活力而又善解人意的女孩在海边漫步。她有着各种方便的语言特性，和一个全面实用的标准库，包括一个特别好用的标准GUI库（在这点上，别的语言无出其右）。她在一个富裕的家庭(Microsoft)长大，而她的父母总是不遗余力的给她佩戴各种首饰，从而让全世界的帅哥回头——我不知道她吸引了多少人，但是她至少吸引了我。

说起C#，不得不提到一位比她出道早，和她长得很像的姐姐——Java。和Java在一起，给我的感觉是，她是大家闺秀，成熟优雅，但是外形略显臃肿。即使是一行的函数，即使没有名字(Anonymous function)，也得写个interface/class来给它包装一番。而且大小姐架子忒大，一个十行不到的class，也得要自己的一个套房(单独文件），就不能和别人share一下？

C++/C#/Java都是重量级的语言，平时要处理个把文件，还真不想劳它们大驾，特累。

对这种事情，我需要一个秘书。我最初雇的是Perl5.xx（据说Perl 6很有进步，但是不太了解），但是它的风格不太对我的胃口，很快我就另觅新人了。然后，我找到了Ruby。这位秘书讨好老板的玩意还真不少（很多syntax sugar）——当然很多是从别人那学来的。刚开始的时候，还真是挺喜欢她的。可是，我这人有一毛病，记性不太好，花里胡哨的东西太多，老记不住。过两天不用，又忘了。最后，我选择了Python，这是个特别爱干净（对代码缩进都有严格要求，否则干脆不伺候）而又很干练的人。没什么很花的东西，但是用起来很顺手。直到现在，我都用它来写普通script。

革命伴侣

MATLAB：我到目前为止，本职工作还是做学术，而不是工程，因此，用得最多的还是matlab。虽然感恩节过去了，还是要对她表示我最衷心的感谢，“没有你，就没有我的今天~~” 周围的人吐了一地。表白完了，还是得说说她的好处。她有着一种特别迷人的气质——不知道迷不迷你，起码迷我——和代数的紧密结合。

计算机发展到今天，曾经出现的语言不知凡几，一种流行的看法是语言背后的思想都是一致的，不同的语言只是换个语法换个库。对于很多语言，这是正确的。但是，对于一种有独特生命的语言，却往往传承着独特的思想，独特的思维哲学。MATLAB正是这样的一种语言。在处理重复操作方面，C/C++之类的传统语言倾向于使用循环，而MATLAB更强调向量化(Vectorization)，把很多运算转化为代数结构，比如矩阵的整体操作。这在思维上，就是需要一个把问题代数化的过程。在不少时候，这是一种挑战，也是一种对数学思维的享受。

从大一开始就使用matlab，到现在也有一些年月了。长期的斗争实践中我和她相濡以沫，也培养了深厚的革命情谊——就在我已经默默地打算和这位气质不凡的她成为革命伴侣的时候，我遇到了Functional Programming。

走进 Functional Programming 的家族

Functional Programming (函数式编程，FP)，是一个大家族。这个家族的历史绝不比主流语言的历史短，起源于上世纪50年代。这个家族的第一个成员，就是大名鼎鼎的Lisp，由图灵奖得主John McCarthy于1958年在MIT最早提出（这位老先生后来去了Stanford）。Lisp最早是个很小的语言，基于它发展出很多分支（方言），最有影响的是Common Lisp和Scheme，前者博大，多用于实际应用；后者精巧，多用于教学和学术研究。 MIT的Sussman教授所写的SICP——被誉为学习Programming的Bible，同时也是MIT CS的经典基础课程6.001的教材——就是基于Scheme。

在来MIT之前有一段空闲时间，我慕名学习了Scheme。这门语言的语法核心非常简单，整个语言的标准全文大约50页，但是却非常灵活，有着令人赞叹的表达能力。这是一位很单纯的小姑娘，她不会让你敬畏，但是却能激发你无穷的想象力。这是一个超越时代的语言，诞生于40年前，却支持着很多后生晚辈很久之后才实现甚至现在还没实现的东西：First-classfunction, Closure, Tail recursion optimization, Lazy evaluation, Pattern-basedSyntax-rule 还有Continuation。但是，这小姑娘太小巧玲珑了，虽然欣赏她却不能用她干多少实际的事情——对实际应用缺乏足够的支持。

在Scheme的引导下，我进入了Functional Programming的家庭，在这个过程中，我开始对它的另外一个成员发生了兴趣，Haskell——她可能是后面几篇文章的主角，在这里先让她出来露个面。过去的两个星期里，我和她频繁约会，亲密接触，欲罢不能。我知道，我又遇到一个让我动心的情人了。

从地球到火星:  和新的情人亲密接触

如果说，用MATLAB让你在一定程度上改变思维，那么，Haskell就是对世界观的彻底冲击，在这里，我所体验到的是一个根本不同的世界。前面的无论是初恋，秘书，伴侣，还是情人，都是地球人；Haskell似乎是来自火星的。

在Haskell的世界里（准确的说，在Pure functional programming的世界里），没有赋值，没有循环，甚至没有顺序执行的语句（不过，可以如果需要的话，可以通过某种方式来模拟出类似的效果），在这里，有一些完全不一样的概念：Pure function(Referential Transparency), Partial Application andCurrying,  Functor,  Folding,  Monad,  Arrow。

在传统的语言里，数据是主要的操作对象，函数一般只是把它apply到输入数据中获取输出。在FP里面，对函数的操作起着核心的作用。在这种语言的代码里，会密集地看到对函数的各种传递，合并，改装，变形。比如下面的情景是很常见的：一个函数作为参数送入一个高阶函数里面，产生出一个新的高阶函数，然后可以用它对别的函数进行变形。。。。。。可能有点晕吧，晕几次后就会发现这个东西写出来的代码very very elegant。你会发现，原来分别要用几十行代码实现的很多看上去千差万别的东西，这这里可以抽象成几行短短的代码统一实现。如果说，传统的语言，一个函数所描述的是某种具体的计算过程；那么，Haskell的每个高阶函数所描述的就是各种表面不同但是蕴含着相似逻辑结构的计算过程的抽象。

话说回来，Haskell能做的东西，不是说别的语言，比如MATLAB/C++之类的不能做。理论上说，实现了Lambda function和Closure的语言，比如C#/MATLAB/Python，都可以肩负起对函数进行合并和改造的任务；而C++的template functor也可以模拟类似的效果。但是，这些语言不是设计出来做这种事情的，让它们去做的话语法上会比较繁琐，思维上也不符合这些语言的主流逻辑，所以很少有人这么写东西——其实，我以前时不时也会这么写，算是一点FP思想的萌芽吧。而Haskell在语言核心上对这些东西提供了直接和强大的支持，在这个世界里，你不这样写，反而成了异类了。

因为之前多多少少运用了一些functional的思想来写程序，我刚接触Haskell的时候并不觉得多不适应，反而，因为它让我很舒服的做一些我以前做起来很繁琐的东西，我很快就觉得这个新的情人特别亲切。可是，跟着她从地球去火星的路，可不是这么好走的，走着走着就开始缺氧了——当我第一次接触Monad这个概念，尤其是State Monad的时候，有好一段时间始终不能appreciate。看了好几个tutorial之后，终于开窍了——一觉醒来，天空还是那么晴朗。之后，再看Monad Transformer和Arrow的时候就心情舒畅了——庆祝自己算是初步融入了火星生活。

值得一说的是，Haskell是我见到的学术色彩非常浓厚的语言，学别的语言，看的是这门语言的教科书。Haskell也有教科书，讲的很多只是初级的东西，看到后面的一些概念，很多都是90年代后才在学术界propose出来的，要学习它们，看的不是书，而是paper。一门要通过academic paper学习的语言，本身就有着不一样的魅力。

我终究还是要在地球上生活的——Haskell在学术上是非常创新的语言，但是，未必特别适合实用——去火星的目的，不是为了定居，而是为了取经。很小很小的时候，大人们告诉我们，站得高看得远，那么站在火星看地球呢？。。。。。。

（也许，在后面的一些文章里，会更详细地分享这个旅程）

Postedby dahuasky  |  12月 6, 2008

回到写paper的日子

来到MIT之后，一年多了，一直埋首学习（各门数学和计算机科学），并且在Alan的引导和John的指导下，逐渐推进自己在理论上的研究，已经远离paper的战场很长时间了。

在今年的CVPR，John觉得需要投一篇，看看来自vision community的feedback。考虑到CVPR是偏重应用性的会议，我们只是基于一些初期的理论，构造了两个应用，完成了这篇paper。

CVPR反映了背后的CV江湖，汤老师曾经说到CVPR发表文章是“华山论剑”——也许，曾经是这样的。如今，这个“华山”上的芸芸众生，不知道看到“四绝”和郭大侠后是否会感到汗颜。说远了。

这次只投了一篇，这是我自参加CVPR以来，单次投出数量最少的——这里并不鼓励“我两个星期前憋出一个idea，然后搞了几套实验”的做法。在HK时，ICCV/CVPR是指挥棒，在这里，研究一直是沿着一条主线，按照自己应有的节奏进行，到了会议来临时的时候，就把部分已经成熟的结果整理发表（这次投的，从理论上说至少是半年前做的东西了）。

在全部实验完成后，我用了三天时间撰写了全文，并自己进行了第一轮修改。我星期一早上10点把draft给John，直到星期四下午6点（deadline前两小时）才把最后一部分改完。因为他是逐个section改好发回，我并行地进行再修改和融入主tex文件，虽然他最后完成时间很晚，但是整体而言时间还是很充裕的，没有匆忙的感觉。

他改稿的认真细致，确实让我挺感动的。星期二下午，当他把改好的introduction发回来的时候，我对照一看，虽然基本思想脉络没有变化，但是，表述上几乎所有句子段落都变了，相当于整个introduction被重写。到了星期三深夜12点，他才发回section 2，这次改动幅度虽然没有intro大，但是重写率也起码超过60%。我当时好奇问他为什么花了这么长的时间，他说我改写后又过了3个pass再发回给你，当时无语。。。最后全部完成时，回头看来，整篇文章改得相当的彻底。以前单独看老外的文章，没觉得他们写出来和我们写的有多大区别，这次John把我的文章修改后，对比一读，“口感”确实相差不少。他在修改过程中表现了非常严谨的作风，几度来找我求证他对于一些技术和数学上的细节的理解是不是正确的——"We should guarantee the correctness of every detail.”

严谨，一直是我努力奉行的治学态度，和John相比，却感到惭愧。在Paper deadline的强大压力下，我很多时候都不自觉地放弃了对严谨的坚持，改用技巧性的学术辞令掩盖问题，对技术细节含糊其词。令人痛心的是，这种风气正在CV广泛蔓延，渐成常态。大家追求流于表面的"novelty”，而不深入问题。我最近翻阅了几十篇近两年的CVPR/ICCV的paper，五光十色，眼花缭乱。这些文章里面确实有一些真知灼见，和有价值的探索，可是，很多却被掩盖于对时髦技术的追逐之中。

研究者工作的最大意义在于做人之所未做，在于引领潮流，而非随波逐浪。谨以此警励自己，并和每一位热爱科学的朋友共勉。

Postedby dahuasky  |  11月 21, 2008

Academia in thisdifficult period

昨天，Susan校长再一次就最近的financial crisis发信给全校。上一次的信是在10月中旬发的，在那次的信中只是说学校将要面对严峻的挑战，要求谨慎地控制支出，以保证学校的financial flexibility。而这次的信是和总教务长联合发出的，显示出问题趋于严重。

信的开头明确指出：

"Yet as the world’s financial markets continue todecline, they forecast a global reduction in resources. In that context, ourchallenge is clear: together we must chart a financially prudent path forward,but one that sustains and fosters the essential character of MIT."

信中说，学校的收入全线受到影响：

"The global economiccontraction will likely compromise all of the Institute’s major revenue streams: endowment,tuition, gifts and research. Market declines have affected even the mostdiversified portfolios, including MIT’s investments,which will reduce the endowment funds available to support our operations."

信很长，提出了很多具体措施去应对这场危机。最核心的一条，就是削减预算。

"Taking all these factorsinto account, we can reasonably anticipate the need to decrease spending by about10-15% over the next two to three years. In the current budget planning cyclefor FY10, we will plan for a base budget reduction of 5%. Future years willundoubtedly require additional cuts by all units."

招聘也将变得极为谨慎。

"We must be very cautious inhiring, relating each hire to core needs, and we should take particular care inmaking decisions that create long-term financial commitments. "

另外，对一栋本科生的宿舍楼(W1)的翻新工程将会暂时搁置。

学校的报纸The Tech上今天用一整版报道了学校的的预算削减计划。学校的本年度预算23亿美元中，其中10忆来源于学校的generalfund，其它的来源于外界的sponsor，其中相当大一部分源于政府拨款。下一年度5%的预算削减涉及的是学校自己的general fund的拨款，而sponsored research不受此影响。文章预测说，如果联邦政府的经济刺激计划获得通过，由sponsored research获得的经费将会获可能获得大幅度增长。

文章还报道了其它学校面临的类似处境

"MIT is among manyuniversities who have proposed sharp spending cuts to help survive the loomingrecession."

具体提到下面一些例子：

• Dartmouth冻结了招聘计划，在两年内将削减预算10%
• Harvard校长说哈佛大学的主要收入来源受到严重影响，下一年endowment可能下降30%
• Stanford将在下一财年削减预算5%

文章最后还是要大家"Don’t panic"：

"MIT graduates are stillhighly sought after."

"There will be tendency forpeople to read this and panic. That’s exactly the wrong reaction. MIT is a place that knows how toadapt."

再来说说我自己的感觉吧。至少到目前为止，学校以及实验室各个部门和各个设施的正常运作没有受到明显的影响。一切工作和活动仍旧如常进行。我只是从新闻报道中感觉危机来临时的气氛。

现在已经进入留学申请的季节。据我所知，有部分朋友对今年的申请形势感到忧虑。至少在表面上看，MIT的招生计划没有受到什么特别影响。校长在两次校长信中都特别指出：

"we will retain ourcommitment to need-blind admission and need-based undergraduate financialaid."

研究生的奖学金也仍旧一切正常。虽然没有明确的迹象表明今年的admission会受到冲击，但是今年的申请还是会不可避免要承受更大的压力：一部分本来即将毕业的学生因为就业形势不佳继续留在学校暂不毕业，这可能导致对新生需求的下降；部分在危机中失去工作的人打算重返校园，因而会加入今年的申请竞争；一些财政积累本来不是很充裕的学校的奖学金发放会受到影响。最终结果如何，等到发offer的时期就会见分晓了。

Information source is available onthe web:

President Susan Hockfield’s Letter to MIT Community

The News in The Tech

Postedby dahuasky  |  11月 19, 2008 

祝贺汤老师当选IEEE Fellow

这两周research方面的工作很繁忙，没有多少时间写blog了。

今天mmlab的朋友告诉我汤老师刚当选为IEEE Fellow，特地上来发文一篇，向汤老师表示热烈祝贺！汤老师最近几年在Vision方面成就卓越，当上fellow实在是众望所归。祝愿他在学术事业上创造新的辉煌。

Postedby dahuasky  |  11月 14, 2008

MATLAB Implementation:light-weight vs. heavy-weight

 

这次，回到一个实际一点的问题，关于matlab的实现。

同一个数学问题，在实际计算中，往往是可能有多种途径的。虽然殊途同归，但是效率很可能大相径庭（即使这些不同途径在理论上有相同的复杂度）。对于小规模计算，这种差别也许无关重要，但是在大规模的simulation或者experiment中，注意不同方式的效率差异可能会让你在跑程序上花费的时间从一天变成一个小时。而且由于计算机字长和精度的限制，选择一个不恰当（但是理论仍旧是正确的）的途径，很可能导致数值溢出。

在这篇文章里，只是以高斯分布的概率密度计算为例子，说明不同计算途径可能导致的不同后果。

在实际问题中，有两种常见的使用高斯模型的情况：

1. 在一个高维空间，使用少数（几个或者几十个）高斯模型；
2. 在一个大型网络中（比如一个图像的每个像素是一个node），在每个节点使用一个（或几个）低维高斯模型。

这两种问题在matlab中的实现需要循不同的路径。

高维高斯模型的pdf计算

在log-scale计算pdf

我们接触许多重要分布（包括Gaussian），在数学上都属于一个类别：Exponential family。当我们需要计算这类分布的概率密度(pdf)时，直接计算概率密度是不明智的，尤其在高维空间。因为 log p(x) 往往会偏离零点甚远的距离，直接计算很可能会导致overflow或者underflow。对于，这类分布，计算log p(x)而不是p(x)本身，应该成为一种惯例。

很多时候，我们的最终目标不是p(x)或者log p(x)，而是由此得到后验概率q(x)。那么给出log likelihood之后，如何计算posteriori呢？最直接的方法是，用exp函数转为p(x)，除以这些p(x)的总和。对于单个样本，MATLAB的实现如下：

% Input loglik:  m x 1 vector with loglik(k) giving log_k p(x)

% Input logpri:  m x 1 vector with logpri(k) giving log-prior of k-th model

% Ouput q:       m x 1 vector with q(k) being the posteriori that the sample is from the k-th model

L = loglik + logpri;

p = exp(L);

q = p / sum(p);

通常在matlab实际应用中，我们不会只计算单个样本，而是大群样本一起计算。那么，就可以用下面的实现(注意bsxfun的运用，它出现在2007a，从此以后被大量运用于矩阵和向量之间的运算，比如把一个向量加到或者乘到矩阵中的每一行或者列，这是新版matlab中最标准和高效的写法)：

% Input loglik: m x n matrix, where loglik(k, i) gives log p_k(x_i),  

% Input logpri: m x 1 column vector, where logpri(k) gives the log-prior of the k-th model

% Output q:     m x n matrix, where q(k, i) is the posteriori that the i-th sample is from the k-th model

L = bsxfun(@plus, loglik, logpri);      % L <- log(prior) + log(likelihood)

p = exp(L);                          % p <- prior * likelihood

q = bsxfun(@times, p, 1 ./ sum(p, 1));  % posterior: q(k,i) = p(k,i) / sum_{l=1}^m p(l,i) 

这在理论上是正确的，但是exp(L)这一步很可能会导致溢出，这也是我们用log-scale的原因。要解决这个问题，关键在于posteriori只取决于p的数值之间的相对比例，而无关于它们的绝对数值。因此，我们可以给各个p同时放大或者缩小到一定的水平，然后再进行计算。对p同时乘以一个因子，相当于给它们的对数同时加上一个常数。这里，我的策略是，给L的每列同时加上一个数，使得它的最大值恰好是零，然后在求posteriori。

L = bsxfun(@plus, loglik, logpri);

L = bsxfun(@minus, L, max(L, [], 1));   % shift each column of L to a safe level

p = exp(L);

q = bsxfun(@times, p, 1 ./ sum(p, 1));

为什么是要控制最大值，而不是最小值呢。道理是这样的：如果最大值是1（i.e. 它的对数是0），那么最小值可能下溢出变成0。但这在posteriori是没关系的，一个模型它的posteriori是0，还是1e-500，都是一回事——这个样本不是从这个模型出来的，在后验概率中，我们只关心对样本有意义的模型。而如果，我们反过来，把最小值调到1，那么最大值可能出现overflow，在matlab里面就是表达成inf，那么后验概率就根本求不出来了。

计算Mahalanobis distance

高斯分布的log-pdf可以写成下面的形式

log p(x) = (1/2) * (d * log(2 *pi) + log det( sigma ) +  (x– mu)^T * inv(sigma) * (x– mu))

这里，d 是维数，mu是均值向量，sigma是协方差矩阵。这个式子有三项，d * log(2 * pi)是一个常数项，在matlab里面计算很直接，这里不讨论了。而后面两项在计算上都有值得注意的问题。

我们首先来看第三项（这一项在数学上叫Mahalanobisdistance）：

(x – mu)^T * inv(sigma) * (x– mu)

对于单个样本，它的直接实现是：

(x - mu)' * inv(sigma) * (x - mu)

对于多个样本，用for-loop显然不是高效的方法。我们可以通过向量化写成：

% X: d x n matrix, with each column being a sample

% D: the difference between the input samples and the mean

% md: 1 x n vector of Mahalanobis distances

D = bsxfun(@minus, X, mu);

md = sum(D .* (inv(sigma) * D), 1);

这里面最重要的一步是inv(sigma) * D的计算，这也是最花时间的地方。对于高维空间，inv(sigma)是很耗时的。这里面有多种策略可以运用于提高运算效率。

1. 如果这种log-pdf的计算要被调用很多次，那么在第一次计算前预先计算好inv(sigma)存放起来，可以有效减少后续计算所需要的时间；
2. 如果只是对整批样本计算一次，那么在MATLAB里面更高效简洁的写法是sigma D。一些刚接触matlab的朋友可能没注意到，matlab里面对于inv(A) * B有着一种功能上等效，但是性能上更好的写法：A B。
3. 如果sigma具有某种特殊结构，那么计算时可以充分利用来提高效率。比如sigma是对角阵的话，那么inv(sigma) * D可以这样计算：

4.  bsxfun(@times, D, 1 ./ diag(sigma));

如果一开始就把sigma存成d x 1的向量，只存放对角线上的值，那么diag(sigma)也省了，而且存储的空间复杂度也从O(d^2)降到O(d)。

对于高维空间，还需要注意的问题是奇异问题。在实际问题中，sigma可能是从样本中估计出来的，在样本量有限的情况下，很可能出现sigma是singular的情况，或者poorcondition。这时就需要考虑regularize或者dimensionreduction，先把sigma变成non-singular的，然后在用上述实现去求log-pdf。

计算log (det (sigma))

在log-pdf中还有一项是log(det(sigma))。这句话可以直接写在matlab里面，理论上是正确的，但是你很可能得到的结果是inf或者-inf，尤其是维数上千的情况。这里面的问题是，一个大矩阵的determinant可能是很大或者很小，以至overflow或者underflow，所以我们只能计算它的对数，而计算路径又不能经过它本身。方法有很多，基于线性代数的原理，我们可以有以下几种策略：

1. 对于一个矩阵，它的determinant就是它的所有eigenvalue的乘积，那么log-determinant就是所有eigenvalue的对数和。给予这个原理，我们可以给予特征值分解实现：

2.  eigvals = eig(sigma);

3.  v = sum(log(eigvals));

类似的，也可以使用奇异值分解SVD。

4. 不过特征值分解或者奇异值分解的复杂度相当高。一种更高效的思路是使用下面的定理: 三角阵的determinant等于对角线上元素的乘积；两个矩阵乘积的determinant等于它们determinant的积。另外，任何一个正定阵，都可以分解为两个三角阵的乘积，这就是矩阵理论中的Cholesky分解。在MATLAB提供了Cholesky分解的非常高效的实现。基于Cholesky factorization，求log-determinant的过程可以表示为

5.  v = 2 * sum(log(diag(chol(sigma))));

这是一种安全高效的实现。即使在det(sigma)保证不溢出的情款下，基于chol分解的实现也不比log(det(sigma))来得慢，比起基于eignevalue的实现则快了很多。对于一般的矩阵（可能非对称），类似的，可以使用LU分解或者QR分解。

大量低维高斯模型的pdf计算

在很多应用里面（比如image modeling)，一种通常的做法是，有大量的低维模型。这里，我们讨论二维的情况。这时我们会有很多不同的covariance matrix，它们都很小。而matlab并没有提供内建的函数，同时对大批矩阵求inverse，求cholesky factorization，或者求determinant。

但是，低维的好处是，它的矩阵的inverse,determinant都有很简单的解析表达式。可以利用它们进行计算：

求一批2 x 2矩阵的determinant

我们知道，一个2 x 2矩阵C的determinant的表达式是：C(1,1) * C(2, 2) – C(1, 2) * C(2, 1)。 基于这点，我们可以对大批矩阵的求determinant，进行向量化：

% Input S: 2 x 2 x m array, with each page giving a covariance

% Output detv: 1 x m array, with v(i) = det(S(:,:,i))

mS = reshape(S, 4, m);

detv = mS(1, :) .* mS(4, :) - mS(2, :) .* mS(3, :);

这种做法，比起用for-loop对每个矩阵逐一计算快很多。

对一批矩阵求inverse

同样的，我们可以给予解析表达式进行计算

invS = [mS(4,:); -mS(2,:); -mS(3,:); mS(1,:)] ./ detv;

invS = reshape(invS, 2, 2, m);

我们看到inv要用到detv的值，所以在实际计算中，应该安排先计算determinant，然后再利用detv去计算inverse。举一反三，对于整个pdf的其它步骤，也可以类似的充分利用解析表达式直接向量化。

对于二维和三维，同过解析表达式向量化是可能的，但是四维以上，虽然仍旧是低维空间，但是解析表达就变得愈发困难。但是，仍旧可以通过各种方式来提高整体的计算效率。而在这里面，采用Expoential family representation比起采用传统的基于mu,sigma的表达更加高效，可以有效实现从estimation到evaluation的全面向量化，并且少数高维模型和大量低维模型为了适应效率要求而产生的在implementation上的差别，可以被重新弥合。关于这个内容，暂时不探讨了。

总的来说，和C/C++不同，MATLAB的实现和数学从来都是密不可分的，高效的实现离不开对数学和数值计算过程的理解。把数学思路充分体现于实现过程中，这是我一直以来特别喜欢matlab的一个重要原因。而反过来，解决计算过程中的效率苦难，也是众多计算科学中的活跃课题。无论是Machine learning，还是optimization，大量的努力其实也就是为了降低一些问题的计算复杂度和提高逼近精度，或者把intractable的问题变得tractable（至少在approximate的意义下）。

 

Postedby dahuasky  |  11月 7, 2008 

Research and Application

受Alan邀请，Michael Jordan来这里访问一些日子。今天听了一个他的seminar，是关于分类的——这是我以前做的领域，内容是f-divergence, surrogate loss function，以及它们的理论上的联系。这主要是他的学生Wainwright完成的工作，在google上可以很容易搜到相关的文章。

Loss function是传统的classification和regression研究的对象， 而divergence则是信息论和信息几何中用于度量两个分布之间的距离的。这个工作揭示了loss minimization和divergence maximization的对偶关系，并且指出了两个不同的loss function在所有数据分布中给出相同的最优解的条件（就是所谓的universalequivalent）。在某种意义上说，这是对于分类问题的一个统一理论。

在Jordan的许多工作中，有一个概念的应用是特别值得注意的，那就是convex duality——这是optimization中的一个核心概念，但是在这些工作中，被巧妙地用于揭示许多内在的理论联系。除了上面的loss和divergence之间的联系之外，convex duality也被用于exponential family的分析。对于Exponential family的分布，它们的log-partitionfunction和negative entropy是互为对偶的，相应的，这种分布的canonical parameter和mean statistics之间也形成一对对偶的参数，因而在某些情况下，求均值的问题，就可以转化为寻求Fenchel conjugate的convex optimization的问题。

无论是Alan还是M. Jordan，他们似乎最关心的都是探讨理论上的课题，最感兴趣的是在数学上具有某种普遍意义的结论，而对于实际应用没有表现出特别的关注。就以上面提到的divergence和loss function为例，它们在NIPS 2005发了一篇文章。整篇文章列出10条定理，但是从头到尾没有一个字的实验。

我平常和Alan开会，他唯一关心的也只是数学上的事情，从不过问实验结果。他的学生们写paper一般也就用一些随机生成数据完成实验，甚至压根就没有实验——他们最关心的是要把定理证明出来。

还有一个让我印象深刻的例子是，一个多月前参加CSAILStudent workshop，一位做算法理论的学生present他的一个新结果：大概是把一个指数复杂度的算法改进成一个多项式复杂度的算法，但是多项式的次数高达接近1000次（抛开实用价值，把指数复杂度降为多项式复杂度，在理论上确实属于重大进展）。他讲完后，台下另外一个同学问他这个东西有什么应用，他很cool的回答说：I don’tcare application!  当时，全场一片掌声和笑声。。。

在这里接触到的这种研究风格，和我以前在MSRA和HK时以实际效能为导向的风格大相径庭。在微软的时候，做出一个东西来，mentor首先是想要看demo，用什么理论是其次的。后来，汤老师当我的导师的时候，看paper也是首先翻到实验结果那里。这一切在来到CSAIL后正好反过来了。当然，MIT是一个非常多元的研究环境，也有着大量工程性很强的实用项目。但是，我自己所处的这个“小圈子”确实是有着非常浓郁的理论色彩，以至于我自己的学习和研究也呈现出偏向纯理论的趋势。但是，我想只要我一天不离开Vision，这种“转型”也就不可能彻底，CV无论从哪个角度说，都是一门应用学科，这点和它上游的Learning不太一样。

——————————————————————————————

也许，这能在一定程度上说明了为什么在很多地方，我们的计算机领域被分成两块：计算机科学(Computer Science)，和计算机工程(ComputerEngineering)。它们之间的gap似乎一直难以愈合。除了技术因素外，更多的也许是因为它们背后所传承的根本不同的理念。科学，探索世界的本原，是一种抽象过程；而工程，追求实用，是一种具体过程。缺乏对实际应用的关怀的纯理论研究，似乎在营造空中楼阁，可是，E=mc^2在它被提出之日，有谁能预测它对世界历史的改变会如此之大呢。

 

Postedby dahuasky  |  11月 6, 2008

生活的脚步没有停下

10月24日刚刚过去了，不知不觉中，生命的时钟又拨过了一年。

今天，朋友们通过msn, email和facebook给我带来了祝福。其中一些朋友，因为各自工作学业繁忙已经疏于联系了，他们没有因此把我遗忘，让我特别感动。谢谢大家，谢谢每一个关心我的人。

在过去的一岁里，我深深的感觉到有两件东西是生活给我们的宝贵财富，需要用心去珍惜：那就是时间和友谊。

上天赋予每个人的生命并不漫长，有太多的事情需要做，希望去做，而时间总是流逝得如此之快。又一岁过去了，似乎做了很多东西，然而扪心自问，自己的努力能真正对得起已经逝去的365天么？时间，不需要花费金钱购买，可是，一旦失去将无可挽回。逝者已矣，来者可追。希望在未来一岁里，时间过得更有意义。

在海外游学的生活远不如在国内和香港来得精彩，在枯寂的生活，繁重的学业之中，唯朋友们常带给我慰藉和鼓励。从香港到北京，从中国到美国，英国，几年来，我们从一个地方，走向了世界各地。维心所系，天涯咫尺。在我快乐的时候，有人分享；在我忧愁的时候，有人分担；在我失落的时候，有人鼓励。生活平静如水，却并不孤独，因为我时刻感觉到和朋友们共同前进。

在人生的驿站中来来往往的人太多，而真正留在生命中的却太少。时间在无情地过滤着生活中的杂质，人际的浮华。经历了时间考验的情谊，所存不多，却弥足珍贵，值得用心去珍惜与呵护。坦荡为人，真诚待友，是我一直恪行的准则。常常希望，以自己所学所能来帮助朋友，以自己的信心和快乐去感染朋友，然而在生活中，总是所得者多，所施者少，内心中对朋友们也总怀着感激和愧疚。在生日之际，我接受了许多朋友的祝福，在这里也祝福朋友们有更大的快乐，幸福和成功。我希望也深信我们共同珍视的情谊在未来的一岁会更加璀璨。

Postedby dahuasky  |  10月 25, 2008 

变换不变性

变换与不变是数学里面最令人神往的一对矛盾统一。所谓“变换不变性”，以不变刻画变化，其核心深刻反映了这种对偶的关系。

变换不变性贯彻于很多具体的数学领域之中，对它的全面讨论远非我力所能及。这篇文章只是讨论它的一个简单例子，希望通过一个小小的窗口管窥这个世界的奥妙。

何谓旋转？

这篇文章只想很初步地回答两个基本的问题

1. 什么叫做旋转(Rotation)？
2. 什么东西被旋转后是不变的（具有旋转不变性）？

为了简单起见，只考虑二维空间，它到高维的推广也并不特别困难。在代数上，所谓旋转，可以用下面的方程表达：

x’ = x cos(t)– y sin(t);   y’ = x sin(t) + y cos(t)。

但是，这样一种表达并不能给人以直观的感觉。所以，我们还是回到几何本身来看待这个问题。什么东西旋转后是不变的呢？“东西”这个概念太模糊了，在数学上，我们讨论问题得首先指定一个范围，就是所谓“对象的集合”。这里，我们先考虑最简单的几何构造——点，我们讨论的全集就是整个二维空间的点集。那么上面的问题，就细化为“哪些点旋转后是不变的？”答案是非常显而易见的，只有一点——就是原点。

这样，我们得到了对于旋转变换的第一个变换不变性：原点不变。可是，这么个条件太宽了，我们很容易找到别的变换，比如缩放，它也是原点不变的。因此，依靠单点的不变性在这里并不能非常有效地刻画变换的特点，我们需要更强大的对不变性的表达。

从“原点不变”到“圆不变”

于是，数学界从对一个点的变换，推广到对一个集合的变换。比如集合 X = {x1, x2,… }, 那么一个变换 T 施加到集合上，得到“变换后的集合”就是：T (X) = { T(x1),T(x2), … }。 如果有 T(X) = X，我们说集合X是变换不变的。 事实上，T(X) 和X 只要包含相同的那堆元素就行了，每个单个的元素都允许被变化到另一点的。

这个推广看似简单，看是表达能力完全不在了一个层次上。比如，一个集合如果有n点的话，它就有2^n个子集，如果只考虑单点，我们只能看n个东西，而如果允许考虑子集的话，我们能看2^n个东西，传递的信息自然也丰富得多。

基于“集合的变换不变性”这个概念，我们可以找到这么一些点集——“以原点为圆心的圆”，它们是旋转不变的。“圆不变”比前面的“原点不变”进步了很多，已经在相当程度上刻画出了旋转的特性，最起码，刚才那个反例“缩放变换”被排除了。如果我们把变换限定为仿射变换（Affine Transform），那么我们已经基于“圆不变性”得到对旋转的严格定义：“旋转就是圆不变的彷射变换”。

“旋转不变的集合”并不仅仅是圆，事实上“不同半径的圆的任意并集”都是旋转不变的，反过来，任何旋转不变的集合都是圆的并集。这样，以“圆”为基(basis)，通过任意并集生成(generate)的集簇(collection of subsets)就对应于全部旋转不变的集合。

这里，我们得到了两个大集合：{所有旋转变换的集合}，{所有圆的集合}，这两个集合都分别同胚于一维实空间，总维数是2，等于原空间的维数——这个结果并非偶然，它其实就是李群论中变换空间，轨迹空间（商空间），和原空间的维数关系定理的一个特例。

我们把讨论的范围限定为仿射变换（包括了平移，旋转，拉伸，缩放和它们的各种合成变换）的情况下，圆不变完整地刻画了旋转变换。旋转（变换）和圆（不变性）构成了一对对偶。

从“旋转——圆”到“变换群——轨迹”

旋转对应于圆，这个我们甚至可以直接观察得到。但是，对于一般的变换呢，我们如何找它们的不变集？这需要把概念推广到：“变换群”和“轨迹”。

一个变换群，就是指一群可逆变换，对于“合成”是封闭的——群里面两个变换的合成必然还在群里。所以，旋转是一个变换群：因为旋转再旋转还是旋转。对于空间一点，把变换群中每个变换都对它施加一下，那么，就可以得到一个集合，叫做“轨迹”。比如旋转群，它（各种角度的旋转）施加于任意一点，就得到一个圆，那么圆就是旋转的轨迹。由于变换群对于合成的封闭性，可以证明，对于任何一个变换群，它施加于任何一点得到的轨迹是变换不变的。这样，我们从“旋转——圆”的对偶关系，进一步推广到了“变换群——轨迹”的对偶关系，从而我们获得了以轨迹刻画变换的方法，这通常比代数方法更为直观和具有更加鲜明的几何意义。

如果变换是自由的，“就是说不同的变换施加于同一点会有不同结果”，那么，变换群和所有轨迹组成的空间（商空间）具有一个结论：它们的维度之和等于原空间维度。这在一定意义上，反映出它们的关系是“互补”的。

概率分布的“变换不变性”

进一步的，我们刚才把变换的对象，从点推广到集合，得到了很多重要的观察。那么，这个事情还可以进一步延伸。假设说，我们有一个空间概率分布，就是一个点以一定的概率出现在空间各处，对这么一个随机点，施加一个变换，在变换后的时刻，得到的点依旧是一个空间分布，变换后的分布是由变换前的分布和变换本身共同决定的。我们也可以这么理解，我们“对整个分布”进行了变换，得到了新的分布。

哪些分布是“旋转不变呢”？就是说，分布旋转后还是同样的分布。我们很容易找到一些：比如标准高斯分布，圆盘里面的均匀分布，等等。为了更清楚地说明这个问题，我们需要更明确的条件。对于连续分布，有一个很容易得到但是很重要的结论：如果这个分布在所有的轨迹上都具相等的概率密度，那么，这个分布是变换不变的。特别的，如果一个分布在每个圆上都是等概率密度，那么这个分布旋转不变。

反过来，标准高斯分布对于一个变换是不变的，那么这个变换是不是必然是旋转呢？

以变换不变性为桥梁，我们可以发现概率分布和几何有着某种内在的联系。一直以来，我们讨论分布时，都关注它的代数形式，而事实上分布的几何形态同样蕴含着丰富的信息，也提供了不同的视角。变换不变性，则是探讨这个问题，从而建立概率论和几何学的联系的一个重要工具。

另外，在随机过程中，对于转移变换的变换不变性，对于描述过程的“各态历经性”(ergodicity)也有着密切的关系。

 

Postedby dahuasky  |  10月 23, 2008 

MATLAB 2008b

一直以来我都在关注着MATLAB的发展，自从MATLAB 2008a发行以来，已经近大半年了，按照MATLAB每年两版的发布规律，2008b应该出来了。今天到Mathworks去看了一下，果然不出所料。发布日期是Oct 9，看来我这次的预感还挺准的，呵呵。

http://www.mathworks.com/products/new_products/latest_features.html

2008a由于系统性地引入了新型的面向对象编程架构，因而相对于之前的版本是一个重大的进展。而2008b对于2008a是属于小范围的增强。其中，令我感兴趣的有这么几个方面

1. 引入了Function browser。我看了一下视频，是一个悬浮的小窗口，里面待一个小搜索拦，你可以很快捷地在里面查找函数和阅读它的几本用法。尤其对于屏幕不大的朋友，编程时在Editor旁边摆一个这个东西，还是有点帮助的。
2. 函数参数的自动提示。这个在VC之类的IDE里面已经不是新鲜的故事了，不过这是第一次做进matlab的编程环境。看来，matlab对于工作环境的人性化有了更多的关注。
3. 全方位增强的文件列表窗口。在以前版本的matlab里面，一直有个Current Directory的小窗口（一般在左边），列出当前目录的文件。不过，那个窗口的功能一直非常有限。在新版里面，这个窗口有了明显的加强，加了类似于Vista的地址栏，能够迅速地在目录之前进行导航。还支持多种浏览方式（大小图标，分组，排序等等）。 另外，还置入一个文件预览的窗口，可以清楚地预览选中文件的基本信息，如果是m文件，预览窗口还会列出里面的函数。总而言之，那个窗口似乎已经发展成了一个五脏俱全的文件管理器和浏览器。

上面的主要是UI方面的改进。而在programing language上，大的改进不多，一个重要的亮点是加入了期待已久的映射表数据结构，在matlab里面，叫做containers.Map，它是一个key/value map。它的功能类似于C++里面的std::map，C#里面的Dictionary，Java里面的Map，或者python里面的dict。matlab宣称，

我以前曾经评论过matlab缺乏高级语言里面的数据结构，比如动态列表，映射表之类的东西。而matlab在2008a引入的新型OOP架构为加入这类结构提供了基础，在2008b中正式加入了第一个高级数据结构，这对于拓展matlab的应用有着重要的意义。containers是一个package，虽然目前只有一个Map类，我相信，matlab的用意肯定不仅仅如此，在后续版本中应该还会加入更丰富的数据结构，比如List， LinkedList，Set之类。我们可以拭目以待。

还有一些别的小改进，比如现在允许多组tic/toc同时计时，对package信息的查询，和对MException的加强，等等。

Statistics Toolbox也进一步加强，

1. 加入了confusionmat函数，用于表示哪类错判到哪类，在分析分类性能时有时会用上。
2. crossval增加了对mean-squared error和misclassification rate作为性能指标的直接支持。
3. 增加了一种叫做NLME的算法：Non-linear Mixture Effects regression model。用于处理非线性回归问题中的混合模型。
   但是总体来说，Statistics toolbox还是不能跟上machine learning的新进展，所提供的函数目前还是以经典统计方法居多。还是希望mathworks能加强对MCMC和Graphical Model的支持

Postedby dahuasky  |  10月 15, 2008

Maths Book List

刚刚创建了一个推荐的数学书的列表（在右边栏），所列的是我看过（有一些只是看过前面一部分）后觉得不错的经典数学教科书，希望对大家有帮助。

 

列表中的图书大致按照这样的顺序编排：往下是比较基础的学科，往上是程度比较高的学科。涉及的数学分支主要有：Analysis, Linear Algebra, Ordinary Differential Equations, ManifoldTheory, Lie Group and Lie algebra, Modern Probability Theory, StochasticProcesses, and Stochastic Differential Equations.

 

每个图书下面的链接都直接连向Amazon的相应页面，大家可以从那里看到更详细的介绍，评论，目录和摘要。

 

这个列表在以后也许会逐步修订扩充，但是应该会基本保持稳定，不会频繁修改。

 

Postedby dahuasky  |  10月 9, 2008

无处不在的线性分解

深刻的思想往往蕴含在简单的数学形式之中。从小至今，对数学的学习一直不断，所学愈多，愈深感现代数学之博大，自己根基之薄弱。在自己所接触的数学之中，各种定理公式纷繁复杂，然细思之下，其核心思想却是非常简洁，但却广泛地以不同形式体现在各个分支之中。事实上，很多不同的数学分支在用自己本领域的语言阐述着一些共同的数学原理。

有三个基本的思想，在我所学到的数学中被普遍的运用：分解，逼近，变换。

• 分解(decomposition)，是和合成(Integration)相互相承的。这里所说的分解思想，其实包括了三个阶段：首先，把一个一般对象，分解成简单对象的组合；然后，对每个简单对象分别加以分析和处理；最后把结果合成为对于原对象的结果。在不同的数学分支里面，分解的形式很不一样，后文中再详述。
• 逼近(approximation)，就是构造简单对象的序列趋近一般对象，并通过这些简单对象的处理和分析结果来逼近一般对象的结果。这种思想在分析(Analysis)主要以极限(limit)的形式存在，是整个分析的根本。在不同的context里面，这种策略的运用有着不同的具体条件和形式，很多时候需要某种形式的一致性(uniformity)来保障结果的正确。比如拓扑学(topology)里面的一致收敛定理(Uniform Convergence Theorem)，测度理论中的单调收敛定理(Monotonic Convergence Theorem)和控制收敛定理(Dominated Convergence Theorem)，概率论中大数定律(Laws of Large Numbers)和分布收敛方面的定理，都体现了这样的思想，而它们则对于各自领域中的函数和各种数学概念的构造起着关键作用。而我们所学的微分，积分，和各种积分变换（比如Fourier Transform)也都建基其上。
• 变换(transformation)，一般是指通过表达形式的变化，揭示出一个数学构造的本征形式，或者使它更适合于某种处理。在代数中的基变换是我们最常见的一种变换方式，它的涵盖很广，除了初等线性代数中讨论的有限维向量的变换，各种对函数的积分变换（Fourier Transform, Laplace Transform, Wavelet Transform）其实也是在一般的函数空间中的基变换。而这种思想还被运用到了概率论中，得到了一个强大的分布分析工具(Characteristic Function)，这其实就是对分布函数的Fourier Transform。对变换的研究，离不开一个很重要的概念——变换不变性(Invariance)，就是要看看在变换过程中什么是保持不变的，这对于刻画一个变换有着极为重要的意义。

——————————————————————————————

线性分解和线性变换的联系

在这篇文章中，只谈谈对分解（最简单的分解——线性分解）的一些理解。在最基本的线性代数中，我们可以把线性空间中的一个向量分解成某些基向量的合成：

x  = c1 e1 + c2 e2 +…

如果施加一个线性变换，那么这个变换的结果，可以通过对每个分量的变换结果组合得到

T(x) = c1 T(e1) + c2 T(e2) +…

这里，我们通过“分解——分别变换——然后合成”的思想来实施这个变换，这有两个需要考虑的要求：

1. 正确性。我们首先需要保证等式左右两边是相等的，事实上这并不是一种必然，它要求T是线性的。从一般的数学意义上说，某种分解策略只适合于某种变换形式，从这个意义上说，分解和变换是相互对应的，在这里，线性分解对应于线性变换。
2. 有利性。等式左边只做一次变换，右边做n次。如果T(e1)和T(x)一样复杂，这纯粹是多此一举。因此，我们希望T(e1), T(e2)是一些更简单的操作，比如只完成一个数乘：T(e1) = a1 * e1。这其实就是特征值分解的一个动机所在。对于某个具体的变换，对应于一个具体的分解（一组具体的基），使得对于每个分量的变换具有简单的形式（在线性空间中就是指数乘了）。

在线性空间中，线性性保证了变换和分解的可交换性，而特征值分解则在正确性的基础上，寻求一种“最优”的分解形式，这种分解形式直接体现了这个变换的本质结构。

这种原理拓展到函数空间，就得到了在工程中广为应用的傅立叶变换(Fourier Transform)。它把一个连续函数分解为实空间的正余弦函数或者复空间的((e^(jwx))的组合。以这些函数为基的原因，就是在线性系统对于这种形式的信号只能进行整体的放大缩小，而不能改变信号内部的结构。从数学的角度说，这些基函数是由线性系统所产生的变换的特征函数。一个复杂的信号处理过程，就因此变为对分量信号分别放大，然后叠加。从Fourier Transform出发，发展出来了一个很大的数学分支，叫做调和分析(HarmonicAnalysis)，对于函数空间的分解进行深入探讨。

线性分解和方程求解

线性分解和合成也是方程求解的重要工具。在初等线性代数中，有一种简单的方程：T x = 0。如果x1, x2, …,都是它的解，那么它们的线性组合也是方程的解。因此，整个解集构成了一个向量空间——变换T的零空间，从而，我们可以通过分析这个空间的基来研究整个解空间的结构。

至于更一般的T x = b的形式，可以通过加一个特解的形式获得解集（其实就是解空间的平移）。因而，其对应的齐次方程Tx = 0仍旧是刻画解集结构的根本所在。

这种想法被沿用于微分方程的求解。因为微分其实是一种线性操作，所以，线性微分方程都可以写成 T x = f的形式，和简单的线性方程不同的是，这里的 T 是由微分算子合成，而 x 和 f 则存在于函数空间之中。但是，解集结构仍旧是T 的零空间的平移。

一个线性变换的零空间，就是它的零特征值对应的空间。这里需要关注 T的特征空间的结构，当T 是一个简单的微分算子 d / dt，它的特征函数 f 应该满足 df / dt = a * x，因此 f( t ) = exp(a * t)。换一句话说，所有如exp(a * t)的指数函数，构成了解空间的基。事实上，这个结论可以继续扩展，exp(a* t)还是高阶微分算子，以及它们的各种线性组合形成的算子的基。

那么我们把一个连续函数沿着这种基分解：f( t ) =c1 * exp(a1 * t) + c2  * exp(a2 * t) +…

解方程得任务，就变成了寻求所有 x(t) = exp(a* t)使得 T x = 0。这代换到方程里面，就转化为代数方程。因此，对于常系数微分方程的求解，当我们得知exp(a * t)是各阶微分算子的特征函数的时候，把解函数沿着它分解，整个事情就变得一目了然了。这样的思路可以直接从上述的标量函数的微分方程推广到向量函数的微分方程——这也是线性系统理论和控制论的基础。

对于更为复杂的积分方程，算子方程，或者随机微分方程，线性分解依旧是方程求解和解空间刻画的核心工具。

概率分布的分解

概率论的基础是测度理论，而它的基础则是sigma-代数，这是一种关于集合的代数（它的运算就是求集合的并集，交集，补集）。测度是给集合一个数值来表达集合的大小，它的构造也体现了分解的三阶段思路：

1. 分解：把集合分解成不相交的简单集合的并集；
2. 分别处理：计算每个简单集合的测度（这个通常相当容易计算）；
3. 合成：把这些测度加起来构成总测度。

我们用 m(A) 表达集合A的测度，那么我们有

m(A1 U A2 U …) = m(A1) + m(A2) +…  (if A1, A2, … disjoint)

这个意思直观理解很朴素：一个东西的大小等于它分成小块后每块的大小之和。上面说到，线性分解对应于线性变换，而这里同样具有一种类似的对应关系：集合的（不相交）分解和测度计算。测度理论的基本公理，就是建立了集合分解和测度计算进行交换的法则。

在概率论里面，最重要的事情之一是求随机变量的期望。如果随机变量在线性空间里面，我们可以对它进行线性分解和合成。另一方面期望满足

E(c1 x1 + c2 x2) = c1 E(x1) + c2E(x2)

这表明了期望是随机变量的线性算子，或者说期望和随机变量的线性分解是可以交换的。因此，上述的分解思想同样运用于期望的运算当中——事实上，对于一般随机函数的期望（勒贝格积分）的定义的构造，正是实施了分解成简单函数——分别计算期望——汇总合成的三阶段思路。最后，通过单调逼近的极限完成完备的构造过程。

期望是进行勒贝格积分的过程，这个过程需要两个概念的参与：随机变量和测度。integral (f du)里面，f 是可测函数（随机变量），u 是测度（概率）。如果我们对u进行一些延伸，从非负测度拓展到带符号测度（可正可负），那么 u 也构成了线性空间（事实上，可以进一步严格证明它是巴拿赫空间 (BanachSpace))。而所有的平方可积的随机函数，则构成另外一个线性空间（进一步，它是一个希尔伯特空间(HilbertSpace)）。它们分别都可以进行线性分解。

在概率论中很重要的Lebesgue-Radon-Nikodym定理其实是对测度进行线性分解的一种形式。我们把全部局部有限的带符号测度构成的空间叫M的话，那么给定一个局部有限测度u，所有对于u绝对连续(Absolutely continuous)的测度自己构成了M的一个子空间，而它的一个补空间则是由相对于u的奇异测度所组成，Lebesgue-Radon-Nikodym分解，则是把一个测度v分解成在这两个子空间中的分量。这种分解形式，对于连续和离散的混成概率有着重要价值。

在传统的概率应用中，我们有一个对象空间，然后在上面建立一个分布模型，然后我们有很多具体的方法去处理。但是，我们如果站在一个不同的角度看待这个问题：所有概率分布构成一个空间，空间中每一个点是一个分布。那么，我们看待一些问题的时候会有不同的高度。在统计学习里面有一个经典的参数估计方法叫最大似然估计(Maximum Likelihood Estimation)，它其实做了一件什么事情呢？就是在上面说的分布的空间中，把由observation所建立的经验分布(empirical distribution）向由某类型分布所组成的流形的投影——这是信息几何(Information Geometry)的最基本的概念。

随机变量的分解

除了对概率进行分解之外，随机变量的分解也有广泛运用，而且通过这种分解建立了概率模型和线性系统的联系。很重要的一个应用就是Markov Process，当初始分布决定之后，概率分布随着时间的演变过程就确定了。如果，我们对初始分布沿着概率传递函数的特征基分解，我们可以获得对整个过程的一个宏观的观察。对应于特征值为1的那个分量一直保持到最后，成为稳态分布；其它分量，会随着时间衰减。其实，这整个过程在数学上所遵循的方程，就是一个线性差分方程（对于离散事件马尔可夫链）或者线性微分方程（对于连续时间马尔可夫过程），这和控制论中研究信号的方程如出一辙。如果我们把分布演变的过程视为信号的变化过程，那么两者的分析可以相互类比。当它们联系起来后，随机过程的学者和控制论的学者的交流可以启发新的思考角度。

在传统微积分里面，我们描述微分的时候，是把一个实数轴分解成很多微小的段。在数学里面，一个重要的学科叫Stochastic Calculus，研究的是随机过程的微分，这需要把随机过程分解成小段。我们希望每个小段的分布形式和整体是一致的，而具有这种特性的分布叫做infinitely divisible。这是研究随机微积分和随机微分方程的重要基础。而我们熟知的高斯分布和泊松分布都具有这样的形式。如果一个随机过程，它对时间的导数符合高斯分布，那么这个过程有一个我们熟悉的名字——布朗运动（Brownian Motion），这是最简单的随机微分方程——也是研究更复杂的随机方程的基础。Stochastic Calculus在金融学用的很多，而在Vision里面颇为少见——事实上，它对于不确定过程的强大表达能力，正好适合对于视觉里面许多充满不确定的过程进行建模。

——————————————————————————————

分解是数学世界里面最重要的思想之一，而线性分解是其中最核心的分解方式。在不同的数学分支中，线性分解把线性空间的元素按照基来分解，在不同的数学分支中，基有着不同的形式，适用于不同的变换：

• 有限维线性代数——基：有限维向量——适用于有限维线性变换
• 信号——基：exp(jwt) or sin(wt) | cos(wt)——适用于线性时不变系统
• 常微分方程——基：exp(at)——适用于微分算子
• 随机变量——基：基本的随机变量——适用于期望（勒贝格积分）
• 随机过程——基：基本的随机过程——适用于随机微分方程（随机积分）

而线性变换的特征值分析的一个重要意义则是为了找出一个能揭示其本征结构的分解形式。特别注意的是，特征值，特征向量，和子空间这些基础概念虽脱胎于有限维分析，但是确可以拓展到对于很多关注无限维空间的学科，成为那些学科进行分析的有力工具。

对于我们的研究来说，分解也提供了非常重要的研究思路，当我们研究一个复杂模型的时候，可以着力于回答几个基本问题：

1. 这个模型的简单形式是什么？是否可以把一个模型分解成简单模型的合成？
2. 深入分析每个简单模型和它的变化？

分离出核心的具有简单形式的基础问题，并致力于此。当我们把简单的模型做深做透之后，有许多数学工具能帮助我们把工作延伸的一般的情况。

Postedby dahuasky  |  10月 2, 2008

关于Alan

Alan不是我的official supervisor，但是由于John和他的密切关系，我每周和他meeting一次，讨论新的研究进展。自从上学期我和他meeting以来，和他的讨论对于我的研究道路产生了很深的影响。很多路子就是在他的引导下走下来的。

Alan Willsky是成就卓著的学者，不过，因为他前期的主要工作都在控制论和随机信号处理上，所以computer vision community可能对他不太熟悉。但是，他和MIT另外一位教授Oppenheim合著的"Signals and Systems”那可就是EE学生无人不晓的经典教材。能得到他的当面指导确实是非常幸运的。

和Alan讨论，让我感受最深的就是他学贯古今的渊博知识，实在令我无比佩服。学者有两种类型，一种是“博”，有宏大视野，了解整个领域的发展态势和主要模型方法的基本思想，但是对数学细节则未必了然；一种是“精”，对于某个topic有很深刻的钻研。二者能做好其一，已经非常不错了。Alan基本是全能。和他讨论这么长的时间，发现他的知识面遍及大量领域：从理论性很强的数学分支：矩阵论，算子论，调和分析，随机分析，微分方程，积分方程，流型理论，李群和李代数，图论，优化理论；到现代科学的重要理论：信息论，系统论，控制论（这是本行），信号处理，机器学习，统计模型，蒙特卡罗方法等等，无一不晓，而且对几乎每个学科都精通数学细节。如此深广积累在我真正接触过的教授中绝无仅有。

他能在学生跟他讲述新进展的时候，及时指出演绎过程的问题。他经常在我们介绍新方法的时候，联系到其它某个领域的思想类似的工作，然后马上在他的大书架中抽出一本教科书，说在40年前在xxx学科针对哪个问题发展了一个类似的工作。正是因为他的这种超强的融汇贯通的能力，引导着我学习了很多别的学科的书籍文献，数学基础也在这个过程中逐渐积累。以前在CVPR/ICCV发了几篇文章，以为自己做了很“前沿”的研究。仅凭以前积累的那几点墨水，在Alan面前实在是惭愧不已（说实话，很多vision top conference的文章在他老人家那根本不入法眼，在他看来最多就是普通学生作业的水平）——只好痛下决心，重铸自己——对于他从我的工作中联系到的那些我不懂得学科（主要是数学），从图书馆找来教材，一门一门的学。

说点题外话，关于Graphical Model和Bayesian Formulation，现在在Vision的文献中用得很多。这个东西在formulate很多应用问题是很好用的，对它的使用确实无可厚非。应该说，把它用在一个新的interesting应用上，是很不错的应用性质的contribution。不过，这中架构严格来说已经不能为其理论价值加分了，formulate graphical model和导出它的inference过程（包括variational inference），属于这里标准的学生作业。

话说回来，Alan最近在做什么研究呢？他的研究兴趣很广，我也不便披露很多具体的东西。有好几个他的学生其实在做一个很“返璞归真”的东西：Gaussian Model，但是做得很有意思。以前也没想到过，高斯分布还有这么深刻的结构，呵呵。相比于很多天天吵着要解决non-Gaussian/non-Linear问题的文章，我觉得，他对于Gaussianmodel的这些研究有价值多了——在最简单的分布里把核心的问题研究清楚了，推广到一般的分布未必是更难的事情。

Postedby dahuasky  |  09月 25, 2008

概率漫谈

前一段时间，随着研究课题的深入，逐步研习现代概率理论，这是一个令人耳目一新的世界。这个世界实在太博大，我自己也在不断学习之中。这篇就算起一个头吧，后面有空的时候还会陆续写一些文章和大家分享我在学习过程中的思考。

概率论要解决的问题

概率论是很古老的数学分支了——探讨的是不确定的问题，就是说，一件事情可能发生，也可能不发生。然后，我们要预计一下，它有多大机会会发生，这是概率论要解决的问题。这里面要特别强调概率和统计的区别，事实上这个区别在很多文章里面被混淆了。举一个简单的例子，比如抛硬币。那么我们可以做两件事情：

1. 我们预先知道抛硬币的过程是“平衡的”，也就是说出现正面的机会和出现背面的机会都是50%，那么，这就是我们的概率模型——这个简单的模型有个名字——伯努利试验(Bernoulli trial)。然后，我们可以预测，如果我们抛10000次硬币，那么正面和背面出现的次数大概各在5000次左右。这种执因“测”果的问题是概率论要解决的，它在事情发生之前进行。
2. 我们预先不知道抛硬币的过程遵循什么法则。于是，我们先去做个实验，抛10000次硬币，数一下正面和反面各出现了多少次。如果各出现了5000次，那么我们可以有很高的信心去认为，这是一个“平衡的”硬币。如果正面出现9000次，反面出现1000次，那么我们就可以基本认为这个硬币遵循一个严重偏向正面的非平衡法则——正面出现的概率是10%。这种执果溯因的事情是统计要解决的，它在事情发生之后进行，根据观察到的情况归纳背后的模型(Model)或者法则(Law)。

这篇文章只讨论概率论的问题。

经典概率的困难

什么是概率呢？长期以来，一个传统而直到今天还被广泛运用的概念是：概率就是一个事情发生的机会——这就是经典概率论的出发点和基础。大部门的初等概率论教科书，给出一个貌似颇为严谨的定义：我们有一个样本空间(sample space)，然后这个样本空间中任何一个子集叫做事件(event)，我们给每个事件A赋一个非负实数P(A)。如果P(A)满足

• P(A) >= 0
• 全集（整个样本空间）的P值为1
• 对于（有限个或者可数个）互不相交的事件，它们的并集的P值等于各自P值的和。这个属性叫可数可加性 (Countable Additivity)

那么我们就称P为概率。这个定义，以及由此而演绎出来的整个经典概率体系，广为接受并被成功用在无数的地方。

但是，这样的定义藏着一个隐蔽很深的漏洞——使得从这个定义出发能在数学上严格导出互相矛盾的结果。假设样本空间是S=[0, 1]，里面的实数依循均匀分布，我们构造这样一个集合。首先，建立一个等价关系：相差值是有理数的实数是等价的。依据这个等价关系，把0到1之间的实数划分为等价类，这样我们有无数个等价类。从每个等价类中随便抽出一个实数作为代表，这些代表构成一个集合，记为H。（注意：我们有不可数无限个等价类，因此这个集合的存在依赖于选择公理(Axiom ofChoice))

那么P(H) 是什么呢？如果P(H)等于零，那么P(S) = 0；如果P(H) > 0，那么P(S) = 无穷大。无论如何，都和P(S) = 1的要求矛盾。这下麻烦大了，我们一直依赖的概率定义竟然是自相矛盾的！

也许，从数学家的眼光看来，这个问题很严重。但是，这对于我们有什么意义呢。我们一辈子都用不着这种只存在于数学思辨中的特殊构造的集合！不过，即使我们从实用出发不顾及这类逻辑漏洞，传统概率论还是会给我们带来一定程度的麻烦。

一个问题，可能大家都有所感觉。那就是，我们在本科学习的概率论中有着两套系统：离散分布和连续分布，基本什么定理都得提供这两种形式，但是它们的推导过程似乎没什么太大差别，一个用求和一个用积分而已。几乎一样的事情，为什么要干两遍呢。

还有，那种离散和连续混合的分布又怎么处理呢？这种“离散连续混合的分布”不仅仅是一种理论可能，在实际上它的应用也在不断增长。一个重要的例子就是狄里克莱过程(Dirichlet Process)——它是learning中的无限混合模型的核心——这种模型用于解决传统有限混合模型中(比如GMM)子模型个数不确定的难题。这种过程，在开始时(t = 0)通常是连续分布， 随着时间演化，在t > 0时变成连续和离散混合分布，而且离散部分比例不断加重，最后（几乎必然）收敛到一个离散分布。这种模型用传统的连续和离散分离的处理方式就显得很不方便了。

事实上，我们是可以把对连续模型，离散模型，以及各种既不连续也不离散的模型，使用一种统一的表达。这就是现代概率论采取的方式。

现代概率论——从测度开始

现代概率论是前苏联大数学家Kolmogorov在上世纪30年代基于测度理论(Measure theory)的基础上重新建立的，它是一个非常严密的公理化体系。什么是测度呢？说白了，就是一个东西的大小。测度是非负的，而且符合可数可加性，比如几块不相交的区域的总面积，等于各自面积之和。这个属性和概率的属性如出一辙。测度理论自从勒贝格(Lebesgue)那个时候开始，已经建立了一套严格的数学体系。因此，现代概率论不需要把前辈的路子重新走一遍。基于测度论，概率的定义可以直接给出：

概率就是总测度（整个样本空间的测度）为1的测度。

测度理论和经典概率论有个很大的不同，不是什么集合都有一个测度的。比如前面构造的那个奇怪的集合，它就没有测度。所以，根据测度理论，样本空间中的集合分成两种：可测的(measurable)和不可测的。我们只对可测集赋予测度或者概率。特别留意，测度为零的集合也是可测的，叫做零测集。所谓不可测集，就是那种测度既不是零，也不是非零，就是什么都不能是的集合。

因此，根据测度理论，我们描述一个概率空间，需要三个要素：一个样本空间，所有可测集（它们构成sigma-代数：可测集的交集，并集和补集都是可测的)，还有就是一个概率函数，给每个可测集赋一个概率。

通过引入可测性的概念，那种给我们带来麻烦的集合被排除在外了。不过，可测性的用处远不仅仅是用于对付那些“麻烦集合”。它还表达了一个概率空间能传达什么样的信息。这里暂时不深入这个问题，以后要有机会写到条件概率(conditional probability)和鞅论(Martingaletheory)时，再去讨论这个事情。这里只是强调一下（虽然有点空口说白话），可测性是讨论随机过程和随机分析的非常重要的概念，在实际计算和推导中也非常有用。

我们看到，这套理论首先通过可测性解决了逻辑上的漏洞。那怎么它又是怎么统一连续和离散的表达的呢？这里面，测度理论提供了一个重要的工具——勒贝格积分(Lebesgue Integral)。噢，原来是积分，那不也是关于连续的么。不过，这里的勒贝格积分和在大学微积分课里面学的传统的积分（也叫黎曼积分）不太一样，它对离散和连续通吃，还能处理既不离散又不连续，或者处处有定义而又处处不连续的各种各样的东西）。

举一个简单例子，比如定义在[0, 1]的函数，它在[0, 0.5)取值为1，在[0.5,1]取值为2。这是一个简单的阶梯函数，期望是1.5。按照传统的黎曼积分求期望，就是把定义域[0, 1]分成很多小段，然后把每小段加起来。勒贝格积分反其道而行之，它不分定义域，而是去分值域，然后看看每个值对应的那块的面积（测度）是多大。这个函数取值只有两个：1和2。那么值为1那块的面积为0.5， 值为2的那块的面积也是0.5，积分就是以这些值为系数，把对应的面积加起来：0.5 x 1 + 0.5 x 2 = 1.5。

上面是连续的情况，离散的呢？假设我们在一个离散集[0,1, 2]上定义一个概率，P(0) = 0.5, P(1) = P(2) = 0.25。对一个函数f(x) = x，求均值。那么，我们看到，值为0, 1, 2对应的测度分别是0.5, 0.25, 0.25，那么我们按照“面积加权法”可以求出：0 x 0.5 +1 x 0.25 + 2 x 0.25 = 0.75。

对于取值范围连续的情况，它通过取值有限的阶梯函数逼近，求取上极限来获得积分值。

总体来说，勒贝格积分的idea很简单：划分值域，面积加权。不过却有效解决了连续离散的表达的统一问题。大家如果去翻翻基于测度理论建立起来的现代概率论的书，就会看到：所谓“离散分布”和“连续分布”的划分已经退出历史舞台，所有定理都只有一个版本——按照勒贝格积分形式给出的版本。对于传统的离散和连续分布的区别，就是归结为它们的测度函数的具体定义不同的区别。

那我们原来学的关于离散分布的点概率函数，或者连续分布的概率密度函数，也被统一了——积分的反操作就是求导，所以那两个函数都叫成了测度积分的“导数”，有一个名字Radon-Nikodym Derivative。它们的区别归结为原测度的具体不同，点概率函数是概率测度相对于计数测度的导数，而概率密度函数则是概率测度相对于勒贝格测度的导数。

我们看到，现代概率论建立了测度概念和概率概念的联系：

• 测度 ———— 概率
• 积分 ———— 期望

谁是基础？概率 vs.期望

从上面的介绍看来，似乎概率（测度）是一个更基本的概念，而期望（积分）是从那引申出来的概念。实事上，整个过程可以反过来，我们可以把期望作为基本概念，演绎出概率的概念。整个概率论，也由此基于期望而展开——其实，如果不是历史惯性，整套理论叫做“期望论”也挺合适的，呵呵。关于这个事情，以后有机会，再做一个更详细的探讨。这里，由于篇幅原因，只提出两个关键点：

1. 如果我们定义了一个期望函数，那么某个子集（事件）的概率就是对它的指示函数的期望。比如一个事件A，它的指示函数IA定义为 IA(x) = 1 当x 属于A, 否则为0。那么A是一个取值要么是0要么是1的随机变量，它的期望就是A的概率。从这个意义上说，所谓概率就是期望的一个简单特例(随机变量是集合的指示函数)。
2. 我们观察到，随机变量的期望符合两个重要性质：
   • 期望是单调的：如果总有 X1 <= X2，那么E(X1) <= E(X2)；
   • 期望是线性的：E(a * X1 + b * X2) = a * E(X1) + b * E(X2)；
3. 所有定义在可测集合上的单调线性实函数E，并且有E(1) = 1，那么E就是一个期望，它施加于任何一个集合的指示函数，就产生那个集合的概率。

有了这么三条，我们可以抛开概率，先定义“期望”这个概念：定义在可测集合上的单调线性实函数。然后，再把指示函数的期望定义成概率。那么，期望就变成了一个更为基本的概念。

事实上，某些新出来的现代概率论的教科书已经处理得更为简洁：直接把“期望”和“概率”看成同一个概念——同时，把几个集合的指示函数和那个集合本身看成一回事。相比于把期望和概率分成两个不同的东西来处理，很多事情的描述和演绎变得非常简洁，而又不损失任何严密性（预先给出期望和概率的一致性的一个严格证明，大概思路是上面三点，不过数学上有一些处理）。由于，把期望视为线性函数，因此对于某个随机变量的期望就变成了有点类似于随机变量和测度的一种类似于“内积”的双线性运算结构。很多本来复杂的概率推演就转化为线性代数演算——不但使得演绎更为方便简洁，而且有助于对于结果的代数特性的更深刻的理解。

总而言之，从经典概率论到现代概率论，发生了两个非常重要的变化：

1. 测度的引入——解决了基础逻辑的难题，统一了离散分布和连续分布。
2. 期望的基础地位——一定程度上消弭了概率和期望的区别，同时把很多概率问题“代数化”。

Postedby dahuasky  |  09月 23, 2008

祝贺母校50岁生日

今天，2008年9月20日，我的母校——中国科学技术大学——迎来了它的50岁生日。

虽然，已经毕业好几年了，但是，每次重回母校，都感觉那是一个让我感到归属感的地方。我走到今天，离不开在科大四年打下的基础。即使毕业以后，我和科大还有着不解之缘。我的硕士导师汤老师，还有在香港时的实验室里的许多同学都是科大的校友。直到今天在MIT，我所在的Eric的小组里面的另外两个中国同学也都来自科大。

在这里，感谢母校和它带给我的一切，祝福母校生日快乐，也祝愿科大的兄弟姐妹，无论正在学校的，还是已经毕业的，共同进步。

Postedby dahuasky  |  09月 20, 2008

Computer Vision的尴尬

Computer Vision是AI的一个非常活跃的领域，每年大会小会不断，发表的文章数以千计（单是CVPR每年就录取300多，各种二流会议每年的文章更可谓不计其数），新模型新算法新应用层出不穷。可是，浮华背后，根基何在？

对于Vision，虽无大成，但涉猎数年，也有管窥之见。Vision所探索的是一个非常复杂的世界，对于这样的世界如何建模，如何分析，却一直没有受普遍承认的理论体系。大部分的研究工作，循守着几种模式：

• 从上游学科（比如立体几何，机器学习，优化等等）获取现成方法，略加变化，套用于某一具体应用。
• 对现有的某个模型方法的一些不足之处，加以改进，比如在formulation中加入或者简并参数，或者调整求解过程。
• 选择多个方法组成一个应用系统。

这些工作实实在在解决了很多问题，功不可没。然其不足在于，一事一法，难成积淀。故此，每年新发表之工作，虽汗牛充栋，蔚为大观，就核心学理，与十年二十年前之状态相比，没有根本突破。

过去一年，在导师们的启发下，涉猎一些其它学科，方知学问之博大，自己以往却是一直坐井观天。在这里其实非常感谢Alan的启发，他一般没有很具体的指导，但是他往往会说“你可以看看某某领域，这个问题可能在几十年前已经被他们在另外一个context下面解决了。”刚开始的时候，我不是很服气——我在Vision的literature的survey表明它在vision里面确实是新问题——不过，当我看到那些领域的文章的时候，不得不佩服Alan的广博知识和对根本不同的领域中的相似问题的洞察力。

我不打算具体讨论一个topic，但是，我建议做vision的朋友在有时间的时候去看看一些表面应用完全不同，但是核心学理却是相通的领域。

• 做Sampling, particle filtering的，不妨看看统计物理学(Statistical Physics），他们对于蒙特卡罗方法已经应用数十年，积累极深，很可能在vision或者learning提出的一些新方法，已经是被他们以另外一种形式或者名称提出过了。
• 做Tracking, video, 和optimization的，可以看看控制论(Control theory)。控制科学对于动态系统（或者其它随时间变化的过程）的研究极为透彻。Alan本来是做控制的，正式他几次强烈的建议下，我才去看动态系统论和控制论，看过一些章节后有如醍醐灌顶。我曾经自己花了不少时间导出的一组矩阵微分方程的解，就是control theory里面已有深入探讨的Peano-Baker series在一定条件下的形式。至于做传导模型或者semi-supervised learning的，控制论中的许多观点和方法也是很有帮助的。
• 做Graphical model，和各种统计模型的，信息论(information theory)是肯定必要的，这个不用我在这啰嗦了。有一门叫做信息几何学(information geometry)，也值得一观。

比较之下方显差距。很多做Vision的朋友都是理论爱好者，喜欢在paper里面列举公式以彰显“理论深度”——可是，我看过的大部分的文章中的公式推演，一般都是循规蹈矩的推导，其水平未必胜于求解一道经典教科书中的数学习题。诚然，这种推理演绎是整个研究中不可缺少的部分，写在文章中也无可厚非，但是，如果仅此则把推演结果列为theoretical contribution，则不免为过了。真正意义的理论贡献者，不在文中公式多寡，也不在数学深浅，而在于是否能对问题的内在原理展开深入剖析，有所发现，言人之未尝言，给人以新的启发。

作为经典物理基础的牛顿三定律，从现在vision领域的眼光看来，不过是对实验的总结，所得结论，除了第二定律有一简单乘法公式（往高深处说，也不过是常系数线性二阶常微分方程）之外，并无太多数学深入其中。虽如此，经典物理的巍峨大厦由此奠定。也许这个例子类比Vision的研究，未必恰当，但是，它起码可以说明，理论贡献之义在于去芜存菁，也就是排开纷繁复杂的表象，发掘那个深刻但是简单的规律。可是，在vision paper宣称的理论贡献中，有多少循此义而行，又有多少在铅华净尽之后留传下来。

纵理论上根基不足，但Vision终究是应用学科，若能广泛应用则其意义必能发扬。虽然经过几十年努力，vision确实在社会生活中有了不少各种应用，不过比起其它学科则相形见拙。且不说诸如通信，软件工程之类早已在全球形成庞大产业，与vision有更多联系的video coding，signal processing, 和medical image，其应用之深广也为vision所望尘莫及。vision没能形成应有的工业应用，一则确实是它面临的实际问题困难重重，实用水平不易达到，二则与我们的研究在相当程度上脱离实际有着很大关联。

以我以往在香港学习时所做的facerecognition来说，这是一个应用性很强的topic，历史也不短，但在实际条件下的识别水平，做这个的朋友也心里明白。很多人在研究这个topic，发表的“新方法”也不少，在paper上识别正确率不达到90%是拿不出手的——可是在那几个标准库（即使是最新的FRGC）上做出的性能和实际的有多大的差距？很多工作assume头像区域都对齐良好，光照条件规则，在此条件下研究出来的算法即使能达到100%的识别性能，在环境极为复杂的条件下能真的应用么？直到今天，大批文章仍在乐此不疲地讨论各种subspace, kernel, svm, boosting的变化花样，却从不思考人脸识别的真正要素所在，难道不是舍本逐末之举。

与此同时，许多在实际工程实践中的trick，为性能提高立下汗马功劳，却因为没有“理论深度”，不登大雅之堂，即使见诸论文，也是在实验部分草略带过。然而，一个方法，无论其最初提出是否有理论依据，如果确实能解决问题，则必有其原因。若能静下心来，暂时忘记那些仅凭思辨就形成的所谓美妙理论，下功夫探究一些确实能解决问题的方法背后所原之学理，其意义不是更大么。也许每个这样的工作都很细小，真能积累下来，假以时日，在推动某个方面的应用上必有实实在在的进益。其中，也可能有机会总结出一些真正有价值的理论。

自诞生以来，Vision的发展已历数十年，不过和许多领域相比，仍处于初始阶段，根基尚显孱弱混乱。唯因如此，对身处其中的研究者，更具挑战意义，而每一个真正的贡献也显得特别有价值。治学之道，不在追逐潮流，而在深原其理。这是新学期新帐号第一次写blog，谨以此，和每一位热爱研究的朋友共勉。

Postedby dahuasky  |  09月 13, 2008

旅程，在新的世界中继续

由于自己的不慎，丢失了已经沿用7年的msn帐号，于此同时，也不得不与曾经见证我过去几年的成长经历的老msn space (http://dahua.spaces.live.com/) 说再见了。

 

失去令人痛心，但是，这也意味着一个新的征程的起航。在未来的日子里，我将在这个新的空间中，继续和朋友们分享我的所闻所思所感。

 

Postedby dahuasky  |  08月 27, 2008

• 林达华博客——笑对人生，傲立寰宇   http://dahuasky.wordpress.com/page/5/
• 林達華教授的homepage：http://www.ie.cuhk.edu.hk/people/dhlin.shtml
• Dahua Lin的各人网站：http://dahualin.org/
• 林达华的github：https://github.com/lindahua
• 增强视觉|计算机视觉 增强现实 http://www.cvchina.info/