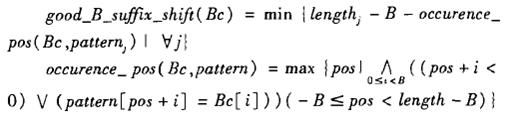Wu-Manber 经典多模式匹配算法

提到多模式匹配算法，就得说一下Wu-Manber算法，其在多模式匹配领域相较于Aho-Corasick算法，就好象在单模式匹配算法中BM算法相较于KMP算法一样，在绝大多数场合，Wu-Manber算法的匹配效率要好于Aho-Corasick算法。这个算法是由吴升（台湾）和他的导师Udi Manber在九十年代提出。当然，要想充分理解WM算法如何加快多模式匹配的效率，还需要对BM算法的深刻了解，可以参考我的另一篇文章《BM算法详解》。

在BM算法中引入的坏字符跳转概念，是BM算法能够在一般应用场景中，效率高于KMP算法的主要原因。WM算法在多模式匹配中，也引入了类似的概念，从而实现了模式匹配中的大幅度跳转。但是在单模式应用场景，很少有哪个模式串会包含所有可能的输入字符，而在多模式匹配场景，如果模式集合的规模较大的话，很可能会覆盖很大一部分输入字符，导致坏字符跳转没有用武之地。所以WM算法中使用的坏字符跳转，不是指一个字符，而是一个字符块，或者说几个连续的字符。通过字符快的引入，扩大了字符范围，使得实现坏字符跳转的可能性大大增加。

WM算法一般由三个表构成，SHIFT，HASH，PREFIX。

SHIFT表就相当于BM算法中的坏字符表，其构建过程有如下几点需要关注

• 我们对模式集合中所有模式的前m个字符构建SHIFT表，其中的m，是模式集合中最短模式的长度值。
• 对于字符块的长度B的选择，我们一般选择2，3个字节。
  
• 在构建SHIFT表的时候，对一个模式p的前m个字符，我们要处理其所有长度为B的子串，并填充对应的SHIFT值，假设字符块大小为B，当前字符快的尾字符与模式前缀的末尾距离为n，则SHIFT[p]=n。以模式abcdefgh为例，假设要处理其前6个字符构成的子串，那么SHIFT[ab]=4，SHIFT[bc]=3，SHIFT[cd]=2，SHIFT[de]=1，SHIFT[ef]=0都要加入SHIFT表中。
• 如果多个模式串前缀，或者同一模式前缀中，有相同的字符块，则保留其中SHIFT值的最小者。比如模式串p1 = abcab，p2=dcabe，其中对于块ab可以计算出三个SHIFT值3，1，0，这里我们需要保留SHIFT[ab]=0。

HASH表就是对应字符块B，所有SHIFT[B]=0的模式与B的映射关系。比如模式串abcde，bcbde，对于块de，他们的SHIFT值都是0，所以他们都由de索引。

实际上，在WM算法中，是可以没有PREFIX表的，但是对于字母文字来说，可能存在多个模式由一个字符块共同索引的情况，如上例，如果存在10个最末两个字符为de的模式串的话，那么在目标串中检索出de组合之后，要用当前的子串逐个尝试匹配这10个模式串，对于算法效率影响很大。所以WM算法同时截取了模式串的一个长度为2或者3的前缀，构建PREFIX表。在执行中缀查找的基础之上，再执行前缀查找，缩小备选模式集，提高匹配效率。如上例，abcde，bcbde，有共同的字符块de，使得SHIFT[de]=0，如果没有PREFIX表，就需要将游标向前移动5位，然后逐一尝试匹配这两个备选模式，如果有了PREFIX表，我们就可以用两个模式的前缀ab，bc再执行一次索引，一般情况下SHIFT值相同，PREFIX也相同的模式串比例很小，本例中二者的前缀是不同的，索引之后就只剩下一个备选模式，此时执行一次字符串比较即可判断当前位置是否发现了匹配模式。

下面用图来描述一下WM算法所要维护的数据结构：

WM算法执行模式匹配的流程如下。

对于目标串target，游标i，模式前缀长度m，字符快长度B，前缀长度C。我们取target[i-B+1...i]，查找其在SHIFT表中的对应值SHIFT[target[i-B+1...i]]，如果找不到，则i+=m-B+1，如果其值为c(c != 0)，那么我们i+=c，再执行上述操作。如果其SHIFT值等于0，我们需要取出target[i-m+1...i-m+C]，然后在SHIFT[de]=0对应PREFIX结合中查找PREFIX[target[i-m+1...i-m+C]]，如果不存在，则将游标i+=1。如果存在则用target[i-m+1]开始的子串，依次匹配满足条件的所有模式串，直到找到匹配模式，或者未发现匹配位置。然后i+=1，继续向后查找。

下面以WM算法对目标串target[1...10]=dcbacabcde，模式结合P{abcde,bcbde,abcabe}，的匹配过程来形象的说明一下。首先，对于模式集合P预处理之后的结果如上面的程序结构图所示。然后从i=5开始执行算法。首先我们发现target[4...5] = ac，SHIFT表中不存在ac，所以i+4，到target[9]，此时发现target[8...9]=cd，SHIFT[cd]=1，所以i+1，然后发现target[9...10]=0，我们取target[6...7]=ab，发现PREFIX[ab]对应的模式串是abcde，然后我们从target[6]开始用目标串与模式串比较，发现匹配模式abcde。

后继：

既然WM算法也是堪称经典的多模式匹配算法，就不能回避与AC算法的比较。

• 从算法的效率角度讲，按照Wu Sun，Manber两人的论文所列的数据，WM算法的性能要明显优于AC算法。
• 从模式集预处理的角度讲，两者的预处理过程都很复杂，但是AC算法由于要维护一个状态机，所以在构建的时间和空间复杂度上，还是要比WM算法更消耗资源。而且AC算法既然要维护自动机，就不得不考虑用什么样的算法来实现自动机的问题，所以自动机的实现方式也会影响AC算法的效果，而WM算法需要考虑的问题就要简单多，一个给力的字典结构足矣。
• 从模式集角度讲，如果模式集动态可变，AC算法动态调整自动机的成本可能要比WM算法高很多。
• 从程序适应性的角度讲，AC算法对于任何模式结合，任何目标串都是O(n)的时间复杂度，而WM算法，对于某些模式集和目标串可能会发生退化现象。

Wu-Manber 经典多模式匹配算法

分类：  Web Security/Javascript  Algorithms2009-05-21 14:56  8095人阅读  评论(7)  收藏  举报

算法 distance function algorithm each 存储

 

多模式匹配的用法，多了去了！DB中对selected patterns进行数挖；安全中对suspicious keyword进行匹配；各种日期形式2009-5-20，2009年5月20日，May,20的搜索；DNA配对；各种replace功能；等等，太口水了枚举这个。

       Wu-Manber基于BM算法思想，如果您佬BM还没OK，请参照我的BM日志搞搞清楚先。

       提到Wu-Manber，其实就是SHIFT、HASH、PREFIX三张表，预处理patterns先把这三张表填好，搜的过程忒简单。

 

1.  拿表说事儿：表干嘛用的

先有个大概印象：SHIFT[]就一跳转表，一张记录向右滑动距离的表。当SHIFT[i]=0时，说明那么多patterns肯定有匹配上的，这时HASH[]和PREFIX[]就要站出来指明谁暂时匹配上了，并对它们通通匹配一番。

 

2.  预处理这一堆patterns：填上三表

这堆patterns长度不一，m=最小长度，该算法也就只检测每pat前m个字符了（那剩余的怎么办呢？o还没想明白）。Patterns长度基本相当最好，假如有一pat掉链子，特短（长度为2），那么每次滑动距离最多也就才2，还滑个什么劲儿呀。所以各pat长度要统一要和谐。

我们把text切成长度为B的块（一般2或3），B怎么算呢？假如有k个pat，那么各pat总长M=k*m，|∑|为c，那么B=log_c(2M)。既然这样，那SHIFT滑动距离就不由末尾单个字符而由末尾B个字符而定了。如果这B个字符跟所有pat都没匹配上，那么很自然小指针可以后滑m-B+1。为什么是m-B+1呢？

 

 

如上图示，虽然XAB不出现在pat末，但它的后缀AB是pat前缀，如果你索性移m=5，那么就错过一个匹配了。其实如果B块不出现在pat末，那么至多它的B-1后缀可能出现在pat前缀，因此，安全的移动距离为m-(B-1)=m-B+1。这其实是相对保守的策略，最后我们会提出改进算法。

 

2.1  SHIFT[]

开SHIFT[]表大小为|∑| ^B，因为要组建长度为B的str，其中每个字符均有|∑|种选择。通过hash function，每个str计算得到一个值index而住进SHIFT。我们现在扫描text的X=x1…x_B, hashFunc(X)=h，那应该滑动多少呢？

如果X跟各pat都没匹配上，那么SHIFT[h]=m-B+1。如果X跟其中某些pat匹配上，那么SHIFT[h]=m-q，其中q是X出现在最右的pat中（假如pat_j）的x_B位置，显然它是最小滑动距离。其实，不用等到实际考查text时再计算SHIFT，我们预处理各pat就可以把SHIFT表填上。对于每个pat，计算其每个长度为B的subpat(a_j-B+1…a_j)的值，SHIFT[hashFun(subpat)]=min{m-B+1,m-j}。

哈哈，于是乎SHIFT[]里记录了text能安全滑过的最大距离，滑的越大当然越快，但是滑的小一点倒也没错。根据这一点，我们可以压缩SHIFT表，把不同的subpat压缩进一个entry，只要值留最小的那个就OK了。（在agrep这个Wu-Manber算法的应用中，B=2时用的原始SHIFT表，B=3时用的压缩SHIFT表）。

 

2.2  HASH[]

只要SHIFT[]>0，那尽管滑text就好了（100个pat的应用中，5%遇到0，1000个时候27%，10000个时候53%）。如果=0，总不至于去跟所有pat一一比对看谁暂时匹配上了吧？o们文明人要用更懒更聪明的方式，去快速锁定那些暂时匹配上的pat们。怎么做呢？HASH！

HASH[i]存放一个指向链表的指针，链表存着这样的pat（末B位通过hash function计算是i）。HASH[]表大小同SHIFT，但相对就稀疏多了，人那儿存着所有可能的组合的SHIFT值。哎，牺牲空间换时间，时空一向两难全。

记现正扫描的text的末B位的哈希值为h。同时引入PAT_POINT（指向实际patterns存储位置的指针链表），该链表按patterns末B位的哈希值排序，那么HASH[h]的值是p（p指向PAT_POINT中哈希值为h的第一个结点处），此时相当于找到第一个跟text末B位匹配上的pat，那么进行匹配，如果匹配不上就继续p++，一直到HASH[h+1]指向的那处地址截止。以上是SHIFT[h]=0的情况。对于SHIFT[h]≠0,那么HASH[h]=HASH[h+1]，因为没哪个pat的末B位能匹配上，自然这两个HASH值应该相等（开始就是结束）。这样，就填好整张HASH[]表了。

 

2.3  PREFIX[]

       如果只有HASH[]表，就囧大了。例如自然语言text中以ing，ion结尾的单词非常多，pat中出现ing/ion结尾的也非常多，如果按HASH[]的方法，那就得HASH[h]~HASH[h+1]的pat一个个匹配。能不能更快些呢？引入PREFIX[]。

       对每一个pat，除了记录其末B位字符的哈希值（PAT_POINT），我们还要记录其首B’位字符的哈希值（PREFIX），一般取B’=2。这是一种有效的过滤手段，因为既末B位相同前B’位也相同的pat很少，这样就没那么多pat需要去匹配了（不像上面那种要一一匹对）。但是也需要权衡啦，因为你计算PREFIX哈希值需要时间，存储它需要空间，换回“一一匹配”的时间，不知划不划算。

 

3.  匹配过程

Step1. 现正扫描的text的末B位t_m-B+1…t_m通过hash function计算其哈希值h。

Step2. 查表，SHIFT[h]>0，text小指针后滑SHIFT[h]位，执行1；SHIFT[h]=0，执行3；

Step3. 计算此m位text的前缀的哈希值，记为text_prefix；

Step4. 对于每个p（HASH[h]≦p<HASH[h+1]）看是否PREFIX[p]=text_prefix。如果相等，方才让真正的pat（即PAT_POINT[p]）去和text匹配。

 

计算SHIFT[],HASH[],PREFIX[]; //开始匹配 while(text<textend) {          hashVal=hashBlock(text);//计算当前块的哈希值          //查找块的坏字符移动表（SHIFT）得到下一个匹配开始位置          shift_distance=SHIFT[hashval]; //③          if(shift_distance==0) //当前块出现在某pat末          {                    shift_distance=1; //①                    p=HASH[hashval];                    //得到可能与当前块匹配的所有pat的集合的开始位置                    while(p)                             检验子集中的pat是否匹配;          }          text+=shift_distance; //② 选择下一个可能的匹配入口 }

 

这里用C给出main()，源码（glimpse代码的一部分）可以从FTP下载：cs.arizona.edu

 

 

 

复杂度O（BN/M），B、M含义同前，N是text字符数。Patterns很短或很少的时候，Wu-Manber不是很牛叉。而成千上万的patterns一起匹配过去，Wu-Manber牛气冲天了。

 

3.  Wu-Manber总结与改进

       一言以闭之：WM是BM处理多模式的派生形式。用的BM算法框架，用块字符来计算的坏字符移动距离（SHIFT[]）；在进行匹配的时候，用的HASH[]选择patterns中的一个子集与当前文本进行匹配，减少无谓的匹配操作。WM不会随着patterns的增加而成比例增长，它远少于使用每一个pat和BM算法对文本进行匹配的时间总和。

 

改进1：

       但是，上文提到过安全的移动距离最大是m-B+1，这是相对保守的策略。其实像图1那种情况的出现次数相对于坏字符情况的出现次数，那真是小乌见大乌了。所以，一次只滑m-B+1多慢呀，能滑m才够快够刺激。呵呵，怎么办呢？想想BM中怎么做地。我们将SHIFT作为坏字符转移表，这样算：

 

 

 

这样，坏字符转移函数的值域0<=y<=m，而不是原来的0<=y<=m-B+1了。下表是SHIFT表的两个版本的实现。SHIFT表空间不变，时间上多了个for循环，总时间是O(B*|∑|+M)，|∑|是块集中块的个数。

 

原始实现：   用m-B+1填写SHIFT表; for each pat {          for pat中每一个块                    计算SHIFT[Bc]; }

改进的实现：   用m填写SHIFT表; for(i=1;i<B;i++) {          对所有Bc∈[suffix(Bc,i)=prefix(pat,i)]                    SHIFT[Bc]=m-i; } for each pat {          for pat中每一个块                    计算SHIFT[Bc]; }

 

改进2：

       WM算法一旦找准匹配入口点，就开始进行“逐个”的比较，能不能用“好后缀”呢？呵呵，可以。引入GBSShift[]，该表记录了每pat的末B位在所有patterns中的所有非后缀出现位置与相应pat_end的距离的最小值。这样就可以快速确定滑动距离。

 

 

 

       GBSShift[]与SHIFT[]大小相同，|∑|。GBSShift[]和SHIFT[]表计算近似，不需额外计算工作，只需复制计算出的SHIFT[]表计算结果，所以它所需的额外时间是O(|∑|)。将WM伪码中的//①改为shift_distance=GBSShift[hashval]即可。

       结合改进1、2，改进算法在处理大规模数据时比WM算法所用时间养活了8~15%。

 

盘点一下：

AC 算法被用于fgrep1.0（在UNIX中通过-f使用）

BM_AC算法在gre中应用，并被fgrep2.0收用。

BMH_AC算法

Wu-Manber算法在agrep中应用，并被glimpse收用。

 

学习自：“A Fast Algorithm For Multi-Pattern Searching”和“一种改进的Wu-Manber多关键词匹配算法”