hdu 4824 Disk Schedule双调欧几里得旅行商问题(dp)

Disk Schedule

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 153    Accepted Submission(s): 86

Problem Description

有很多从磁盘读取数据的需求，包括顺序读取、随机读取。为了提高效率，需要人为安排磁盘读取。然而，在现实中，这种做法很复杂。我们考虑一个相对简单的场景。
磁盘有许多轨道，每个轨道有许多扇区，用于存储数据。当我们想在特定扇区来读取数据时，磁头需要跳转到特定的轨道、具体扇区进行读取操作。为了简单，我们假设磁头可以在某个轨道顺时针或逆时针匀速旋转，旋转一周的时间是360个单位时间。磁头也可以随意移动到某个轨道进行读取，每跳转到一个相邻轨道的时间为400个单位时间，跳转前后磁头所在扇区位置不变。一次读取数据的时间为10个单位时间，读取前后磁头所在的扇区位置不变。磁头同时只能做一件事：跳转轨道，旋转或读取。
现在，需要在磁盘读取一组数据，假设每个轨道至多有一个读取请求，这个读取的扇区是轨道上分布在 0到359内的一个整数点扇区，即轨道的某个360等分点。磁头的起始点在0轨道0扇区，此时没有数据读取。在完成所有读取后，磁头需要回到0轨道0扇区的始点位置。请问完成给定的读取所需的最小时间。

 

Input

输入的第一行包含一个整数M（0<M<=100），表示测试数据的组数。
对于每组测试数据，第一行包含一个整数N（0<N<=1000），表示要读取的数据的数量。之后每行包含两个整数T和S（0<T<=1000，0<= S<360），表示每个数据的磁道和扇区，磁道是按升序排列，并且没有重复。

 

Output

对于每组测试数据，输出一个整数，表示完成全部读取所需的时间。

 

Sample Input

   
   
   
   

    
    
    
    3
1
1 10
3
1 20
3 30
5 10
2
1 10
2 11
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    830
4090
1642
   
   
   
   

 

Source

2014年百度之星程序设计大赛 - 资格赛

 

Recommend

liuyiding

思路【转】：

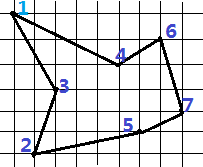
  欧几里得旅行商问题是对平面上给定的n个点确定一条连接各点的最短闭合旅程的问题。如图（a）给出了一个7个点问题的解。这个问题的一般形式是NP完全的，故其解需要多于多项式的时间。

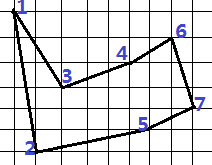
J.L. Bentley 建议通过只考虑双调旅程(bitonic tour)来简化问题,这种旅程即为从最左点开始，严格地从左到右直至最右点，然后严格地从右到左直至出发点。下图(b)显示了同样的7个点的最短双调路线。在这种情况下，多项式的算法是可能的。事实上，存在确定的最优双调路线的O(n*n)时间的算法。

 图a            图b

注:在一个单位栅格上显示的平面上的七个点。 a)最短闭合路线,长度大约是24.89。这个路线不是双调的。b)相同点的集合上的最短双调闭合路线。长度大约是25.58。

这是一个算导上的思考题15-1。

首先将给出的点排序，关键字x，重新编号，从左至右1，2，3，…，n。

定义p[i][j]，表示结点i到结点j之间的距离。

定义d[i][j]，表示从i连到1，再从1连到j，（注意，i>j，且并没有相连。）

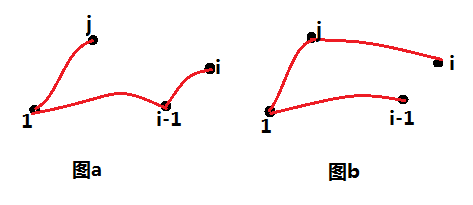
对于任意一个点i来说，有两种连接方法，一种是如图（a）所示，i与i-1相连，另一种呢是如图（b），i与i-1不相连。

根据双调旅程，我们知道结点n一定与n相连，那么，如果我们求的d[n][n-1]，只需将其加上p[n-1][n]就是最短双调闭合路线。

根据上图，很容易写出方程式：

dp[i][j]=dp[i-1][j]+dist[i][i-1];

dp[i][i-1]=min(dp[i][i-1],dp[i-1][j]+dist[j][i]);

/*************************************************************************
	> File Name: hdu-4824-Disk_Schedule.cpp
	> Author: nealgavin
	> Mail: nealgavin@126.com 
	> Created Time: Sun 25 May 2014 07:38:59 PM CST
 ************************************************************************/

#include<iostream>
#include <cstdio>
#include <cstring>

using namespace std;

const int mm = 1000+9;
const int oo = 1e9;

int dp[mm][mm],d[mm];
int n;

int dis(int x,int y)
{
    if(d[x] < d[y])
        x^=y^=x^=y;
    int distance = d[x]-d[y];
    return min(distance,360-distance);
}

void init()
{
    dp[1][0] = dis(0,1);
}

int DP()
{
    for(int i=2;i<=n;++i)
    {
        dp[i][i-1] = oo;
        for(int j=0;j<i-1;++j)
        {
            dp[i][i-1] = min(dp[i][i-1],dp[i-1][j]+dis(i,j));
            dp[i][j] = dp[i-1][j] + dis(i,i-1);
        }
    }
    int ans = oo;
    for(int i=0;i<n;++i)
        ans = min(ans,dp[n][i]+dis(i,n));
    return ans;
}
int main()
{
    int cas;
    while(~scanf("%d",&cas))
    {
        while(cas--)
        {
            scanf("%d",&n);
            int x;
            d[0] = 0;
            for(int i=1;i<=n;++i)
                scanf("%d %d",&x,&d[i]);
            init();
            printf("%d\n",DP()+x*800+n*10);
        }
    }
    return 0;
}