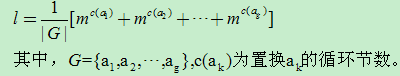普通涂色问题 组合数学-Polya定理
Polya定理是组合数学理论中最重要的定理之一。该定理是要解决这样的问题,在一个集合内,定义了一个等价关系,人们往往关心由这个等价关系所决定的等价类的数目。
Polya定理:
设有n个对象,G是这n个对象上的置换群,用m种颜色涂染这n个对象,每个对象涂染一种颜色。若一种染色方案在群G的作用下变为另一种方案,则这两种方案当作是一种方案。那么存在的方案个数为:L=∑mc(ai)/|G|
公式中:|G|就是这个对象的个数。c(ak)是置换ak的循环节数。
概念补充:
1、什么是置换?
这就是一个置换,把群(1 2 3 4 5)置换成(3 5 1 4 2),这就是一个置换。
2、什么叫置换的循环节?
在上面这个置换中看到,1置换为3,同时3又能置换为1,这就是一个循环。4置换为4本身,这也算一个循环。所以上面的置换可以写成这样:
左右两个表示是等价的,从后面的表示可以清楚的看到每个循环,以及循环节的个数。
3、怎么求一个置换的循环节数?
方法一:把所有置换写出来,就能知道它们的循环节数了。
方法二:现成公式,对于旋转,有c(ai) = gcd(n,i),i为转动幅度,1~n,gcd是求最大公约数。
典型题目:用2种颜色去染排成一个环的6个棋子,如果通过旋转得到则只算一种,一共有多少种染色方案?
典型的满足polya公式的条件,m=2,n=6。因为是旋转得到的置换,所以存在6个置换(自己置换到自己也算)。
每个置换的循环节已经标出了。
所以根据polya定理公式可以算出,染色方案数为 (2^6+2^1+2^2+2^3+2^2+2^1)/6 = 14