利用OpenGL点精灵实现云模拟(Cloud Simulation Using OpenGL PointSprite)
利用OpenGL点精灵实现云模拟
Cloud Simulation Using OpenGL PointSprite
这篇教程介绍一种利用OpenGL点精灵,也就是PointSprite来实现云的模拟。在网上找了一些资料和论文,都是模拟真实的云和光照,且都比较复杂。后来看到一篇文章,介绍了一篇相对简单但效果比较好的方法。首先建立好云的轮廓模型,可以使用3DMax或其他的建模工具,然后创建该模型的包围体,将包围体中属于云的部分抽取出来,最后对抽取出来的部分进行三角化,然后贴图,最后加上光照。受到该方法的启发,这里我介绍一种更为简单的方法来实现对云的模拟。
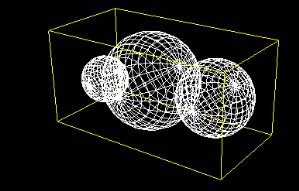
和从文件读取云模型相比,用代码生成云的轮廓要快的多。云的轮廓我们可以用球来模拟,使用多个不同大小的球可以组成不同形状的云。图Fig1中显示了利用三个半径不同的球组成的云的形状。当然你也可以使用更多不同大小的球来组成更逼真,更复杂的云。
|
|
| Fig1. 不同大小的球组成的云的形状 |
描述这样三个球只需用几个结构体即可。
| struct VECTOR3 { float x,y,z; VECTOR3(){} VECTOR3(float _x, float _y, float _z) { x = _x; y = _y; z = _z; } }; |
结构体VECTOR3是一个三维向量结构体,用来表示球的圆心。再加上半径R我们就可以描述球的几何性质了。于是球的结构体可以定义为
| struct Sphere { VECTOR3 C; float R; Sphere(){} Sphere(VECTOR3 c, float r) { C.x = c.x; C.y = c.y; C.z = c.z; R = r; } }; |
接下来就要得到整个云的包围盒,包围盒可以用包围盒立方体对角线上的两个顶点来描述,这里使用顶点坐标全为负和全为正的两个点。包围盒机构体可以定义为
| struct BoundingBox { VECTOR3 origin; VECTOR3 MinPt; VECTOR3 MaxPt; Line Boundaries[12]; }; |
在上面的结构体中,origin表示包围盒的中心坐标,MinPt表示全为负的顶点,MaxPt表示全为正的顶点。利用球心所在位置和球半径就可以决定包围盒的大小。用每一个球的球心位置减去该球的半径,然后比较这个值,最小的就是MinPt的值。同样用每一个球的球心位置加上该球的半径,其中最大的就是MaxPt的值。为了方便后面绘制该包围球,该结构体中还有一个Line结构体,该结构体表示包围盒的边的信息,定义如下
| struct Line { VECTOR3 origin; VECTOR3 end; };
|
很明显Line结构体中origin和end分别表示包围体一条边的起点和终点。Fig2显示了Fig1中云形状的包围盒。
Fig2. 云的包围盒
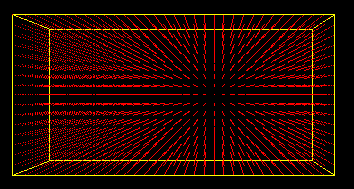
为了用PointSprite来模型云,我们需知道每个PointSprite在三维空间中的位置。而这些位置就是由云的形状来决定的。只要能找到每个球内的PointSprite,那么就能利用PointSprite来模拟云的形状了。这里用的方法有点体渲染(Volume Rendering)的味道。先将包围盒分成一个一个的体素(voxel),voxel的多少由voxel的大小来决定。现在要做的就是抽取出所有球内的voxel。
抽取的过程很简单,只要判断当前voxel和球的位置关系即可。将voxel的坐标带入球的方程(已知球心和半径),判断和半径的关系,只要小于等于半径的平方,那么该voxel就在球内。
(x-a)2+(y-b)2+(z-c)2 ≤ R2
上式中(a,b,c)为球心,R为半径。
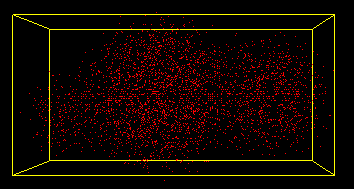
Fig3 从包围盒中抽取云轮廓内的体素
从Fig3中可以看到,(a)中显示了包围盒的所有体素,(b)中抽取出了在云形状内部的部分体素。(c)中可以清楚的看到云内部体素的形状,而(d)则是将云内部每个体素的位置加上一定随机扰动的结果。
有了云内部voxel,就可以将每个voxel当作一个PointSprite,适当的调节PointSprite的大小和体素的大小,然后给PointSprite贴上带alpha通道的纹理即可,如Fig4。
Fig4 PointSprite模拟的云
整个云模拟的过程中,重要的部分就是将包围盒中用于模拟云的球内部的体素抽取出来。只要正确的抽取出云内部的体素,那么云的形状也就得到了。具体的内容是实现方法可以参考该教程的源代码。如果OpenGL版本不支持PointSprite,请更新OpenGL驱动,并下载高版本的OpenGL库。