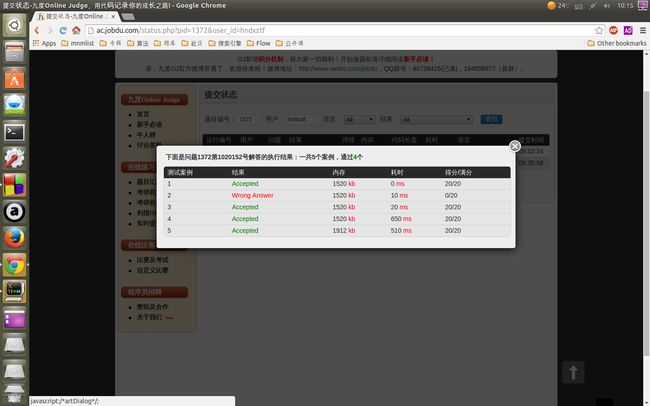
九度_题目1372：最大子向量和（连续子数组的最大和）

//有点小操蛋,所有已想到的测试用例都可以通过,奈何奈何,就是最后不能通过,无力

//测试的边界条件非常非常重要.....

//对了,这题主要是了解的什么是动态规划,这个思想挺好挺好...

题目描述：

HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天JOBDU测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢？例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。你会不会被他忽悠住？
输入：
输入有多组数据,每组测试数据包括两行。
第一行为一个整数n(0<=n<=100000),当n=0时,输入结束。接下去的一行包含n个整数(我们保证所有整数属于[-1000,1000])。
输出：
对应每个测试案例,需要输出3个整数单独一行,分别表示连续子向量的最大和、该子向量的第一个元素的下标和最后一个元素的下标。若是存在多个子向量,则输出起始元素下标最小的那个。
样例输入：
3
-1 -3 -2
5
-8 3 2 0 5
8
6 -3 -2 7 -15 1 2 2
0
样例输出：
-1 0 0
10 1 4
8 0 3

#include<iostream>
#include<stack>
using namespace std;
int main()
{
    int num;//the num of the array
    while(cin>>num&&num!=0)
    {
        stack<int>st;
    int temp=0;
    int index=0;//to store the begin of the max  subarray
    int max=0;//to install the max sum
    int *array=new int [num];
    cin>>array[0];
    st.push(0);
    for(int i=1;i<num;i++)//caculate the subsum of the subarray
    {
        cin>>array[i];
        if(array[i]+array[i-1]>=array[i])
        {
            if(array[i-1]<0)
                st.push(i);
            else
                array[i]=array[i]+array[i-1];
        }
        else{
            st.push(i);
        }
    }
    max=array[0];
    for(int i=1;i<num;i++)//caculate the max num and the index
    {
        if(max<array[i])
        {
            max=array[i];
            temp=i;//the end index of the max subarray
        }
    }
    while(!st.empty())//caculate the beginning index of the max subarray
    {
        if(st.top()>=temp)
        {
            st.pop();
        }
        else
        {
            index=st.top();
            break;
        }
    }
    cout<<max<<' '<<index<<' '<<temp<<endl;
    delete array;
    }
 
    return 0;
}
 
/**************************************************************
    Problem: 1372
    User: hndxztf
    Language: C++
    Result: Wrong Answer
****************************************************************/