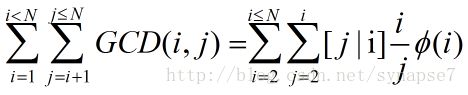UVa 11417 GCD (欧拉φ函数)

11417 - GCD

Time limit: 2.000 seconds

http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&category=24&page=show_problem&problem=2412

Given the value of N, you will have to find the value of G. The definition of G is given below:

 

Here GCD(i,j) means the greatest common divisor of integer i and integer j.

 

For those who have trouble understanding summation notation, the meaning of G is given in the following code:

G=0; for(i=1;i<N;i++) for(j=i+1;j<=N;j++) {     G+=GCD(i,j); } /*Here GCD() is a function that finds the greatest common divisor of the two input numbers*/

 

Input

The input file contains at most 100 lines of inputs. Each line contains an integer N (1<N<501). The meaning of N is given in the problem statement. Input is terminated by a line containing a single zero.  This zero should not be processed.

 

Output

For each line of input produce one line of output. This line contains the value of G for corresponding N.

 

Sample Input                 Output for Sample Input

10 100 500  0

67 13015 442011

如何求?

思路：可以直接算，复杂度O(N^2 logN)，但是我们可以找到一种复杂度更小的算法O(N loglogN)

以10为例，与之互素的有φ(10)=4个(1,3,7,9)，与之gcd=2的有φ(10/2)=4个(2,4,6,8)，与之gcd=5的有φ(10/5)=1个(5)

这样，10提供的G值就是5*φ(2)+2*φ(5)+φ(10)=5+8+4=17

根据上述计算过程可以得到如下公式：

（方括号指艾弗森约定，当方括号内语句为真时其值为1，假时为0，参见《具体数学》P21）

完整代码：

/*0.013s*/

#include<cstdio>
const int maxn = 501;

int phi[maxn], G[maxn];

void init()
{
	int i, j;
	for (i = 2; i < maxn; ++i)
		phi[i] = i;
	for (i = 2; i < maxn; ++i)
	{
		if (phi[i] == i)
			for (j = i; j < maxn; j += i)
				phi[j] = phi[j] / i * (i - 1);///计算欧拉φ函数
		for (j = 1; j * i < maxn; ++j)
			G[j * i] += j * phi[i];
	}
	for (i = 3; i < maxn; ++i)
		G[i] += G[i - 1];
}

int main()
{
	init();
	int n;
	while (scanf("%d", &n), n)
		printf("%d\n", G[n]);
	return 0;
}

转载请注明： http://blog.csdn.net/synapse7/article/details/12882087