PCA实现步骤及其与opencv中PCA实现方式的对比
PCA(Principal Components Analysis,中文名叫主成分分析,是数据降维很常用的算法。按照书上的说法是:寻找最小均方意义下,最能代表原始数据的投影方法。PCA的一个经典应用就是人脸识别,感兴趣的可以在网上搜eigenface。
PCA的主要思想是寻找到数据的主轴方向,由主轴构成一个新的坐标系,这里的维数可以比原维数低,然后数据由原坐标系向新的坐标系投影,这个投影的过程就可以是降维的过程。
原理网上一搜内容很多,这里推荐一篇讲原理讲得不错的文章: http://www.csdn123.com/html/blogs/20130320/180.htm 大家可以参考。下面着重讨论PCA的实现,由于我主要是在做图像处理时用的PCA,所以以对图像进行降维来说明。
1 对训练集图像进行处理
读取测试集中的所以图像,然后将其保存在一个矩阵中。如果图像个数为m,图像长宽为i、j,则我们创建矩阵A(m, n = i*j)用来保存图像数据。数组的每一行表示一个图像的所有像素信息,每一列表示一个维度,也即不同图像在同一位置的像素信息,降维也即用更少的列来代表图像。
经过对训练集的图像进行处理后,所有的图像都在表示在了一个矩阵中,我们假设这个矩阵是data。则data的维数为m*n,其中n=i*j,及n为一张图像的所以像素点。
2 求平均值mean
在data矩阵中每一个维度上的平均值,具体方法为对data矩阵的每一列求平均值mean。如果是人脸识别的话,这一步得到的就是mean face(平均脸)。
3 每列减去均值
将data矩阵的的每列减去该列的均值,这样每列的数据均值为0。我有用C来表示相减的值,及C=data-mean
4 计算协方差矩阵
协方差矩阵表示不同随机变量之间的相互关系,图像中也即求任意两个像素之间的关系。如果两个随机变量的协方差为正或为负,表明两个变量之间具有相关性,如果为零表示两个变量不相关。通过计算协方差矩阵,我们就可以获得不同像素之间的关系。针对人脸识别,计算的协方差矩阵大小为n*n,其中n表示图像的像素点个数。
计算协方差的矩阵具体操作的A = C' * C/n,这里C‘为C矩阵的转置。注意这里有个除n。在后面代码中会提到。
5 计算协方差矩阵A的特征值和特征向量
由于协方差矩阵是实对称阵,所以可以求得其所有的特征值和特征向量,其共有n个特征值和特征向量。
6 选择主成分(投影矩阵)
所谓主成分即是具有最大特征值的特征向量,所以我们需要将特征向量按照特征值由大到小排序,然后根据精度要求选择不同数量的特征向量,例如我们选择了前pca_dim个特征向量,通常pca_dim远小于n(在我们的人脸识别实验中,为了达到95%的精度,pca_dim只有72,而n为120*140=17040)。
这里我们所选择的主成分实际上就是投影矩阵,我们用project_mat表示。project_mat的维度为n*pca_dim.
7 将训练集进行降维
此步骤将原始的训练集进行降维变换,方法就是对原始矩阵用project_mat进行投影。
原始的图像数据data是m*n的矩阵,投影后就成了n*pca_dim的矩阵(每一列都是一个特征向量)。
特别注意这里投影时并不是想网上很多博客中所说的data*project_mat。正确的方法应该是C*project_mat,及(data-mean)*project_mat。
8 将测试集进行降维
同步骤6相似,读取所有的测试集图像,然后对其也进行降维操作。如果测试集有M幅图像,则降维后的矩阵为M*pca_dim。
注意对测试集进行降维时也不是直接用测试集的data*project_mat,正确的做法应该是测试集的(data-mean)*project_mat。
下面是我写代码对PCA的实现,其中有与Opencv中自带的计算PCA方法的对比。
注意为了方便对矩阵的操作,我在代码中使用的开源的Eigen库,Eigen是个很方便的数学出来工具,尤其是对矩阵的处理。
Eigen库的主页http://eigen.tuxfamily.org/index.php?title=Main_Page
使用Eigen也很简单,下载好开源包后,直接在工程的属性页面“附加包含目录”把Eigen的目录添加进去。配置好后在在代码中添加#include”Eigen/Eigen”和using namespace Eigen两行就可以使用了。
#include<iostream>
#include<fstream>
#include"Eigen/Eigen"
#include<opencv2\opencv.hpp>
using namespace Eigen;
using namespace std;
using namespace cv;
void BubbleSort(float *pData, int Count);//冒泡排序
const int num = 5; // 样本数量
const int dim = 10; // 样本的维度(一张图片的维度)
const int pca_dim = 4;// pca dimension of each sample
int main()
{
// 原始数据:每一行代表一个样本(这里为了测试时随机生成的)
MatrixXf data =MatrixXf::Random(num, dim);
// 求每一维度上的平均值,即每一列的平均值,最后求出来是一个行向量
MatrixXf mean =data.colwise().mean();
cout<<"------------------Orignal data-------------------------\n"<<data<<endl;
//cout<<"----------------Mean------------------\n"<<mean<<endl;
MatrixXf C(num, dim); // data-mean
MatrixXf C_T(dim, num);// C的转置
for(int i=0; i<num; i++)
{
C.row(i) =data.row(i)-mean; //C= data-mean
}
C_T =C.transpose();
/*
协方差矩阵A的维度为dim*dim,这里除不除dim最后结果都一样,
在书中的定义中是要除的,估计是有数学含义的。
*/
MatrixXf A =C_T*C;
EigenSolver<MatrixXf> sol_A;
sol_A.compute(A);
//求协方差矩阵的特征值和特征向量
MatrixXf eigenvals_A =sol_A.eigenvalues().real();
MatrixXf eigenvecs_A =sol_A.eigenvectors().real();
//排序
float a[dim]={0.0};
for(int i=0; i<dim; i++)
{
a[i] =eigenvals_A(i, 0);
}
BubbleSort(a, dim);
MatrixXf sorted_eigenvals_A(dim, 1);
MatrixXf sorted_eigenvecs_A(dim, dim);
//对特征值从大到小排序
for(int i=0; i<dim; i++)
{
sorted_eigenvals_A(i, 0) =a[i];
}
//对应的改变特征向量的排序
for(int i=0; i<dim; i++)
{
for(int j=0; j<dim; j++)
{
if(eigenvals_A(i, 0) == a[j])
{
sorted_eigenvecs_A.col(j) =eigenvecs_A.col(i);
}
}
}
//求PCA的投影矩阵及降维结果
MatrixXf project_mat(dim, pca_dim); //投影矩阵
MatrixXf res(num, pca_dim); //最终输出,维度为num*pca_dim
for(int i=0; i<pca_dim; i++) //抽取主成分
{
project_mat.col(i) =sorted_eigenvecs_A.col(i);
}
/*
res就是原始数据降维后的矩阵
特别注意,这里是C*project_mat,即(data-mean)*project_mat
在网上看到很多人这里都是直接用的data*project_mat,那样是不对的
*/
res =C* project_mat;
//-----------------------------OpenCV中的PCA--------------------------------//
CvMat *pca_input =cvCreateMat( num, dim, CV_32FC1); // 输入
CvMat *pca_avg =cvCreateMat( 1, dim, CV_32FC1); // 平均值
CvMat *pca_eigenvalue =cvCreateMat( 1, std::min(num, dim), CV_32FC1); // 特征值
CvMat *pca_eigenvector =cvCreateMat( std::min(num, dim), dim, CV_32FC1);// 特征向量
CvMat *pca_eigenvector_T =cvCreateMat(dim, std::min(num, dim), CV_32FC1); // 特征向量
CvMat *pca_output =cvCreateMat(num, pca_dim, CV_32FC1); // 输出
// 数据导入
for(int i=0; i<num; i++)
{
for(int j=0; j<dim; j++)
{
cvSetReal2D(pca_input, i, j, data(i, j));
}
}
cvCalcPCA(pca_input, pca_avg, pca_eigenvalue, pca_eigenvector, CV_PCA_DATA_AS_ROW);
cout<<"\n---------------Eeigen Tool降维结果-----------------"<<endl;
cout<<res<<endl;
cout<<"---------------OpenCV Tool降维结果---------------"<<endl;
cvProjectPCA(pca_input, pca_avg, pca_eigenvector, pca_output);
// 数据输出
for(int i=0; i<num; i++)
{
for(int j=0; j<pca_dim; j++)
{
float temp =0.0;
temp =cvGetReal2D(pca_output, i, j);
cout<<temp<<" ";
}
cout<<endl;
}
system("pause");
return 0;
}
//冒泡排序算法
void BubbleSort(float *pData, int Count)
{
float iTemp;
for(int i=1; i<Count; i++)
{
//一共进行(count-1)轮,每次得到一个最大值
for(int j=Count-1; j>=i; j--) //每次从最后往前交换,得到最大值
{
if(pData[j]>pData[j-1])
{
iTemp = pData[j-1];
pData[j-1] = pData[j];
pData[j] = iTemp;
}
}
}
}
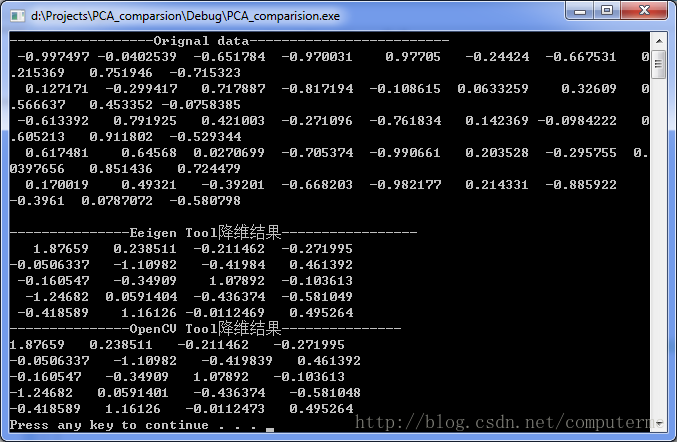
最后通过对比,发现用Eigen自己实现的PCA与Opencv实现的PCA结果的数值是一样的,但是有些向量的符号相反。
编译好的代码下载:http://download.csdn.net/detail/computerme/7497923
PS:可能有的读者发现了有些博客中讲PCA降维时,在第一步生成原始的data矩阵维度为dim*m(dim为一个图像的维度,m为训练集图片的张数)。
如果是这种情况的话,则上面的A 应该等于 C*C' (C'是C矩阵的转置),最后求降维后的矩阵时公式也应该变为project_mat的转置乘以(data-mean)。
总之,不管data矩阵的维度是dim*m还是m*dim,我们都要确保第四步求得的协方差A的维度是dim*dim。因为协方差矩阵表示的就是data中各维度的关系。
**************************************************************************************************************************