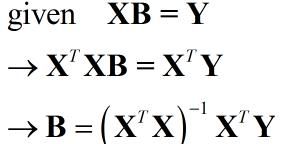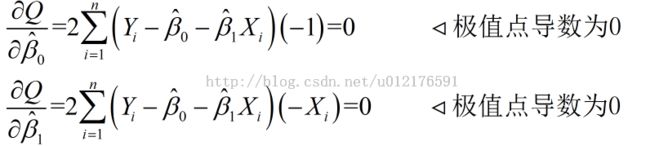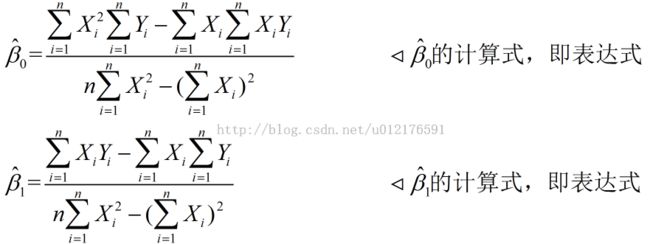最小二乘法的一般形式和矩阵形式原理推导和代码实现

作者:金良([email protected]) csdn博客:http://blog.csdn.net/u012176591
1.线性代数模型
首先给出最小二乘解的矩阵形式的公式:
推导过程:
条件:
若A为m×n的矩阵,b为m×1的矩阵,则Ax=b表达了一个线性方程组,它的normal equation的形式为ATAx=ATb。
当Ax=b有解时(即矩阵[A|b]的秩与A的秩相同),Ax=b与ATAx=ATb的解集是一样。
而当Ax=b无解时,ATAx=ATb仍然有解,其解集即最小二乘解(least squares solution),即使得(Ax-b)T(Ax-b)的值最小的解,可以理解为使方程组Ax=b近似成立且误差最小的解。
Python语言写的一个例子:
#encoding=UTF-8
'''
Created on 2014年6月30日
@author: jin
'''
from numpy import *
import matplotlib.pyplot as plt
from random import *
def loadData():
x = arange(-1,1,0.02)
y = ((x*x-1)**3+1)*(cos(x*2)+0.6*sin(x*1.3))
#生成的曲线上的各个点偏移一下,并放入到xa,ya中去
xr=[];yr=[];i = 0
for xx in x:
yy=y[i]
d=float(randint(80,120))/100
i+=1
xr.append(xx*d)
yr.append(yy*d)
return x,y,xr,yr
def XY(x,y,order):
X=[]
for i in range(order+1):
X.append(x**i)
X=mat(X).T
Y=array(y).reshape((len(y),1))
return X,Y
def figPlot(x1,y1,x2,y2):
plt.plot(x1,y1,color='g',linestyle='-',marker='')
plt.plot(x2,y2,color='m',linestyle='',marker='.')
plt.show()
def Main():
x,y,xr,yr = loadData()
X,Y = XY(x,y,9)
XT=X.transpose()#X的转置
B=dot(dot(linalg.inv(dot(XT,X)),XT),Y)#套用最小二乘法公式
myY=dot(X,B)
figPlot(x,myY,xr,yr)
Main()
程序截图:
MATLAB写的例子:
clear
clc
Y=[33815 33981 34004 34165 34212 34327 34344 34458 34498 34476 34483 34488 34513 34497 34511 34520 34507 34509 34521 34513 34515 34517 34519 34519 34521 34521 34523 34525 34525 34527]
T=[1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30]
% 线性化处理
for t = 1:30,
x(t)=exp(-t);
y(t)=1/Y(t);
end
% 计算,并输出回归系数B
c=zeros(30,1)+1;
X=[c,x'];
B=inv(X'*X)*X'*y'
for i=1:30,
% 计算回归拟合值
z(i)=B(1,1)+B(2,1)*x(i);
end
Y2=[]
for j=1:30,
Y2(j)=1/(B(1,1)+B(2,1)*exp(-j));
end
plot(T,Y2)
hold on
plot(T,Y,'r.')
截图:
2、一般线性模型
一般线性模型,即普通最小二乘法( Ordinary Least Square,OLS):所选择的回归模型应该使所有观察值的残差平方和达到最小。
以简单线性模型 y = b1t +b0 作为例子。
回归模型:
最优化目标函数:
则目标函数可以简化成如下形式:
对简化后的目标函数进行求解,得到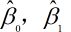 表达式:
表达式:
下面是C++的实现例子:
#include<iostream>
#include<fstream>
#include<vector>
#include<cstdlib>
#include<ctime>
using namespace std;
class LeastSquare{
double b0, b1;
public:
LeastSquare(const vector<double>& x, const vector<double>& y)
{ //下面是最小二乘法的核心过程
double xi_xi=0, xi=0, xi_yi=0, yi=0;
for(int i=0; i<x.size(); ++i)
{
xi_xi += x[i]*x[i];
xi += x[i];
xi_yi += x[i]*y[i];
yi += y[i];
}
b1= (xi_yi*x.size() - xi*yi) / (xi_xi*x.size() - xi*xi);
b0 = (xi_xi*yi - xi*xi_yi) / (xi_xi*x.size() - xi*xi);
}
double getY(const double x) const
{
return b0+b1*x;
}
void print() const
{
cout<<"y = "<<b0<<"+"<<b1<<"x "<<"\n";
}
};
int main()
{
srand((unsigned int)(time(NULL)));//
vector<double> x,y;
double xi = 0,yi,xin,xout;
for (int i = 0;i <10; i++) {
yi = 2*xi +1;//原模型
yi += 0.05*rand()/RAND_MAX*yi;//添加噪声
y.push_back(yi);
x.push_back(xi);
xi += 5.0;
}
LeastSquare lsObj(x, y);//用样本数据实例化对象
lsObj.print(); //输出最小二乘法得到的模型
cout<<"Input x:\n";
while(cin>>xin)
{
xout = lsObj.getY(xin);//利用得到的模型计算因变量
cout<<"y = "<<xout<<endl;
cout<<"Input x:\n";
}
}
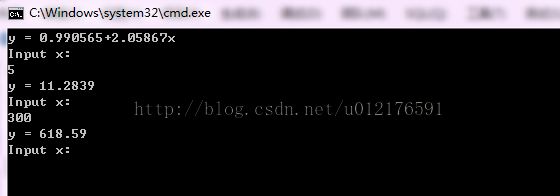
执行效果截图:
3.最小二乘法和梯度下降算法
相同点:
1 、本质相同:两种方法都是在给定已知数据(因变量 & 自变量)的前提下对因变量算出出一个一般性的估值函数。然后对给定的新的自变量用估值函数对其因变量进行估算。
2、 目标相同:都是在已知数据的框架内,使得估算值与实际值的差的平方和尽量更小(事实上未必一定要使用平方),估算值与实际值的差的平方和的公式为:
不同点:
1、实现方法和结果不同:
最小二乘法是直接对error求导找出全局最小,是非迭代法。
而梯度下降法是一种迭代法,有一个学习的过程,先由给定参数计算一个error,然后向该error下降最快的方向调整参数值,在若干次迭代之后找到局部最小。
梯度下降法的缺点是到最小点的时候收敛速度变慢,并且对初始点的选择极为敏感,其改进大多是在这两方面下功夫。
- http://isites.harvard.edu/fs/docs/icb.topic515975.files/OLSDerivation.pdf
- http://web.stanford.edu/~mrosenfe/soc_meth_proj3/matrix_OLS_NYU_notes.pdf
- http://users.wfu.edu/cottrell/ecn215/ols.pdf
- http://www.le.ac.uk/users/dsgp1/COURSES/THIRDMET/MYLECTURES/2MULTIREG.pdf