原文地址:http://www.cnblogs.com/kuangbin/archive/2011/07/26/2117636.html
最近又复习了下最大流问题,每次看这部分的内容都会有新的收获。可以说最大流问题的资料网上一搜一大把,根本没有必要自己写;但是大部分资料上的专业术语太多了,初学很难理解,至少我当年学这部分的时候前几次就没有看懂。所以我准备备份一点个人的理解。
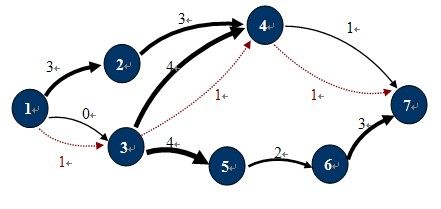
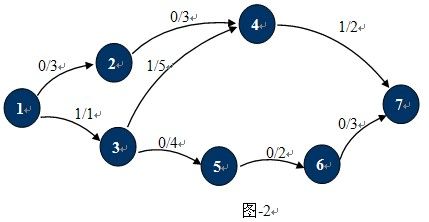
如图-1所示,在这个运输网络中,源点S和汇点T分别是1,7,各边的容量为C(u,v)。图中红色虚线所示就是一个可行流。标准图示法如图-2所示:
其中p(u,v) / c(u,v)分别表示该边的实际流量与最大容量。
关于最大流
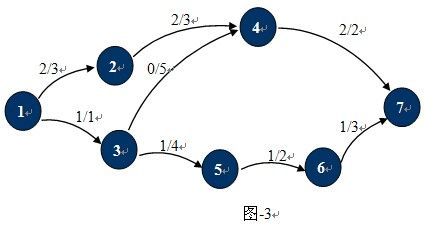
熟悉了什么是网络流,最大流也就很好理解了。就是对于任意的u∈V-{s},使得p(s,u)的和达到最大。上面的运输网络中,最大流如图-3所示:MaxFlow=p(1,2)+p(1,3)=2+1=3。
在介绍最大流问题之前,先介绍几个概念:残余网络,增广路径,反向弧,最大流定理以及求最大流的Ford-Fulkerson方法。
残余网络 增广路径 反向弧
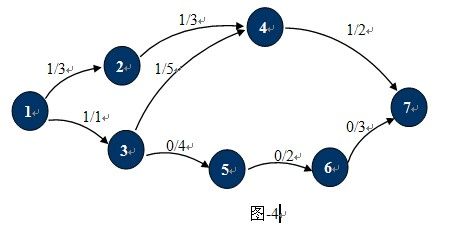
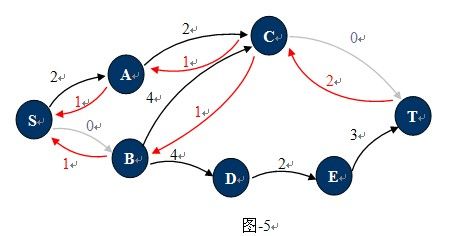
观察下图-4,这种状态下它的残余网络如图-5所示:
也许现在你已经知道什么是残余网络了,对于已经找到一条从S 到T的路径的网络中,只要在这条路径上,把C(u,v)的值更新为C(u,v)-P(u,v),并且添加反向弧C(v,u)。对应的增广路径Path为残留网络上从S到T的一条简单路径。图-4中1,2,4,7就是一条增广路径,当然还有1,3,4,7。
此外在未做任何操作之前,原始的有向图也是一个残余网络,它仅仅是未做任何更新而已。
最大流定理
如果残留网络上找不到增广路径,则当前流为最大流;反之,如果当前流不为最大流,则一定有增广路径。
Ford-Fulkerson方法
介绍完上面的概念之后,便可以用Ford-Fulkerson方法求最大流了。为什么叫Ford-Fulkerson方法而不是算法,原因在于可以用多种方式实现这一方法,方式并不唯一。下面介绍一种基于广度优先搜索(BFS)来计算增广路径P的算法:Edmonds-Karp算法。
算法流程如下:
设队列Q:存储当前未访问的节点,队首节点出队后,成为已检查的标点;
Path数组:存储当前已访问过的节点的增广路径;
Flow数组:存储一次BFS遍历之后流的可改进量;
Repeat:
Path清空;
源点S进入Path和Q,Path[S]<-0,Flow[S]<-+∞;
While Q非空 and 汇点T未访问 do
Begin
队首顶点u出对;
For每一条从u出发的弧(u,v) do
If v未访问 and 弧(u,v) 的流量可改进;
Then Flow[v]<-min(Flow[u],c[u][v]) and v入队 and Path[v]<-u;
End while
If(汇点T已访问)
Then 从汇点T沿着Path构造残余网络;
Until 汇点T未被访问