凸包及旋转卡壳求凸包直径
那么,先提一下最基本最暴力的求凸包直径的方法吧---枚举。。。好吧。。很多问题都可以用 枚举 这个“万能”的方法来解决,过程很简单方便是肯定的,不过在效率上就要差很远了。 要求一个点集的直径,即使先计算出这个点集的凸包,然后再枚举凸包上的点对,这样来求点集直径的话依然会在凸包上点的数量达到O(n)级别是极大的降低它的效率,也浪费了凸包的优美性质。不过在数据量较小或者很适合时,何必要大费周折的用那些麻烦复杂的算法呢,枚举依然是解决问题的很好的方法之一。
然后就是今天的旋转卡壳算法了。(那个字念 qia 。。。搞了好久才发现读都读错了。囧。。。)
旋转卡壳可以用于求凸包的直径、宽度,两个不相交凸包间的最大距离和最小距离等。虽然算法的思想不难理解,但是实现起来真的很容易让人“卡壳”。
被一对卡壳正好卡住的对应点对称为对踵点,对锺点的具体定义不好说,不过从图上还是比较好理解的。
可以证明对踵点的个数不超过3N/2个 也就是说对踵点的个数是O(N)的
对踵点的个数也是我们下面解决问题时间复杂度的保证。
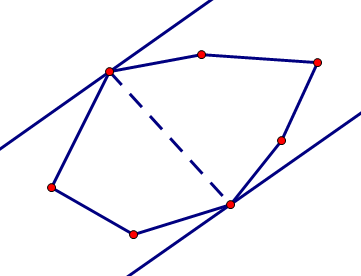
卡壳呢,具体来说有两种情况:
1.
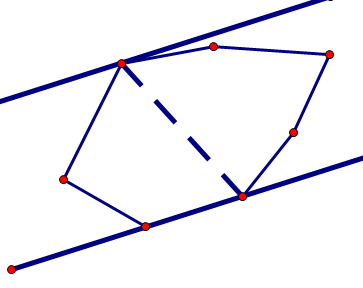
2.
而第二种情况在实现中比较容易处理,这里就只研究第二种情况。
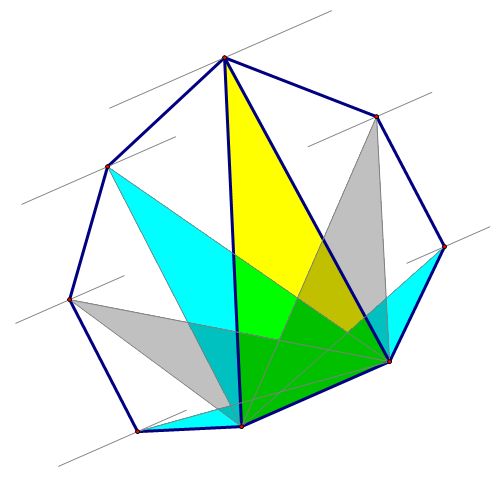
在第二种情况中 我们可以看到 一个对踵点和对应边之间的距离比其他点要大(借用某大神的图··)
也就是一个对踵点和对应边所形成的三角形是最大的 下面我们会据此得到对踵点的简化求法。
下面给出一个官方的说明:
Compute the polygon's extreme points in the y direction. Call them ymin and ymax. Construct two horizontal lines of support through ymin and ymax. Since this is already an anti-podal pair, compute the distance, and keep as maximum. Rotate the lines until one is flush with an edge of the polygon. A new anti-podal pair is determined. Compute the new distance, compare to old maximum, and update if necessary. Repeat steps 3 and 4 until the anti-podal pair considered is (ymin,ymax) again. Output the pair(s) determining the maximum as the diameter pair(s).
根据上面的第二种情况,我们可以得到下面的方法:
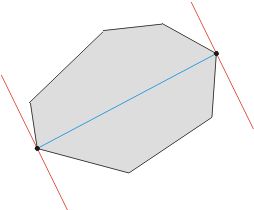
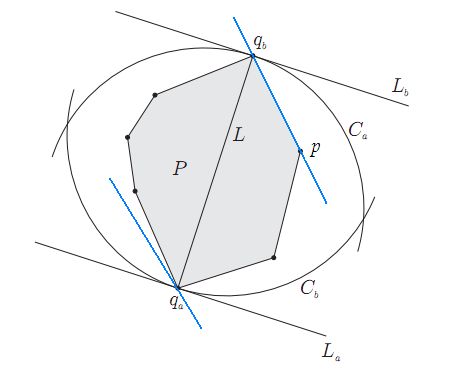
如果qa,qb是凸包上最远两点,必然可以分别过qa,qb画出一对平行线。通过旋转这对平行线,我们可以让它和凸包上的一条边重合,如图中蓝色直线,可以注意到,qa是凸包上离p和qb所在直线最远的点。于是我们的思路就是枚举凸包上的所有边,对每一条边找出凸包上离该边最远的顶点,计算这个顶点到该边两个端点的距离,并记录最大的值。
直观上这是一个O(n2)的算法,和直接枚举任意两个顶点一样了。
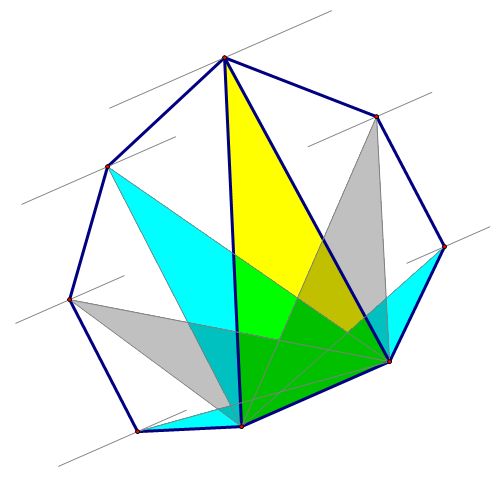
然而我们可以发现 凸包上的点依次与对应边产生的距离成单峰函数(如下图:)
这个性质就很重要啦。
根据这个凸包的特性,我们注意到逆时针枚举边的时候,最远点的变化也是逆时针的,这样就可以不用从头计算最远点,而可以紧接着上一次的最远点继续计算。于是我们得到了O(n)的算法。这就是所谓的“旋转”吧!
利用旋转卡壳,我们可以在O(n)的时间内得到凸包的对锺点中的长度最长的点对。
又由于最远点对必然属于对踵点对集合 ,那么我们先求出凸包 然后求出对踵点对集合 然后选出距离最大的即可
http://poj.org/problem?id=2187
AC代码:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<string>
#include<cstring>
#define N 50005
using namespace std;
struct Point
{
int x;
int y;
}p[N];
int top,n,s[N];//s中存的是凸包包含的极点
int dis(const Point& a,const Point& b)
{return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);}
int cross(const Point& a,const Point& b,const Point& c)
{return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y);}
bool cmp(const Point& a,const Point& b)//幅角排序
{
int ans=cross(p[0],a,b);
if((ans>0)||(ans==0&&dis(p[0],a)<dis(p[0],b))) return true;//再求凸包时可以删除共线的那个点
return false;
}
void graham()//凸包模板
{
s[0]=0;
s[1]=1;
top=1;
for(int i=2;i!=n;++i)
{
while(top&&cross(p[s[top-1]],p[s[top]],p[i])<0) top--;
s[++top]=i;
}
top++;
}
void doit()//旋转卡壳
{
int q=1,ans=dis(p[s[0]],p[s[1]]);
for(int i=0;i!=top;++i)
{
while(abs(cross(p[s[(i+1)%top]],p[s[i%top]],p[s[(q+1)%top]]))>abs(cross(p[s[(i+1)%top]],p[s[i%top]],p[s[q%top]]))) q=(q+1)%top;
ans=max(ans,max(dis(p[s[(i+1)%top]],p[s[q]]),dis(p[s[i%top]],p[s[q]])));
}
printf("%d\n",ans);
}
int main()
{
while(~scanf("%d",&n))
{
for(int i=0;i!=n;++i)
scanf("%d%d",&p[i].x,&p[i].y);
Point ans=p[0];
int u=0;
for(int i=1;i!=n;++i)
if((ans.y>p[i].y)||(ans.y==p[i].y&&ans.x>p[i].x)) ans=p[i],u=i;
if(u) swap(p[u],p[0]);
sort(p+1,p+n,cmp);
memset(s,0,sizeof(s));
graham();
doit();
}return 0;
}