一致性哈希算法 - Consistent Hashing
http://itindex.net/detail/46061-%E5%93%88%E5%B8%8C-%E7%AE%97%E6%B3%95-consistent
一致性哈希算法 - Consistent Hashing
标签:
哈希 算法 consistent | 发表时间:2013-10-15 21:49 | 作者:dreamrealised
出处:http://blog.csdn.net
一、简单介绍一致性哈希算法
分布式存储中,常常涉及到负载均衡问题,由于有多个数据存储服务器。因此当一个对象被保存时候,它究竟应该存放到哪个数据存储服务器上面呢?这就是负载均问题。
![]()
又例如:现在假设有一个网站,最近发现随着流量增加,服务器压力越来越大,之前直接读写数据库的方式已经不能满足用户的访问,于是想引入 Memcached 作为缓存机制。现在一共引入三台机器可以作为 Memcached 服务器,那么究竟缓存到哪台服务器上面呢?
可以用简单哈希计算:h = Hash(object key) % 3 ,其中 Hash 是一个从字符串到正整数的哈希映射函数,这样能够保证对相同 key 的访问会被发送到相同的服务器。现在如果我们将Memcached Server 分别编号为 0、1、2,那么就可以根据上式和 key 计算出服务器编号 h,然后去访问。但是,由于这样做只是采用了简单的求模运算,使得简单哈希计算存在很多不足:
1)增删节点时,更新效率低。当系统中存储节点数量发生增加或减少时,映射公式将发生变化为 Hash(object key)%(N±1),这将使得所有 object 的映射位置发生变化,整个系统数据对象的映射位置都需要重新进行计算,系统无法对外界访问进行正常响应,将导致系统处于崩溃状态。
2)平衡性差,未考虑节点性能差异。由于硬件性能的提升,新添加的节点具有更好的承载能力,如何对算法进行改进,使节点性能可以得到较好利用,也是亟待解决的一个问题。
3)单调性不足。衡量数据分布技术的一项重要指标是单调性,单调性是指如果已经有一些内容通过哈希计算分派到了相应的缓冲中,当又有新的缓冲加入到系统中时,哈希的结果应能够保证原有已分配的内容可以被映射到新的缓冲中去,而不会被映射到旧的缓冲集合中的其他缓冲区。
由上述分析可知,简单地采用模运算来计算 object 的 Hash 值的算法显得过于简单,存在节点冲突,且难以满足单调性要求。
于是,我们引入一致性哈希算法:Consistent Hashing, 是一种 hash 算法,简单地说,在移除/添加一个服务器时,它能够尽可能小地改变已存在的 key 映射关系,尽可能地满足单调性的要求。下面就按照 5 个步骤简单讲讲 Consistent Hashing 算法的基本原理。
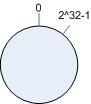
步骤一:环形 hash 空间
考虑通常的 hash 算法都是将 value 映射到一个 32 位的 key 值,即 0~2
32
-1 的数值空间。我们可以将这个空间想象成一个首( 0 )尾(2
32
-1)相接的圆环,如下图所示。
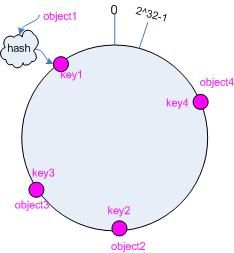
步骤二:把对象映射到 hash 空间
接下来考虑 4 个对象 object1~object4,通过 hash 函数计算出的 hash 值 key 在环上的分布如下图所示。
步骤三:把服务器映射到 hash 空间
Consistent Hashing 的基本思想就是将
对象和服务器都映射到同一环形的hash 数值空间区域(并存在这个区间内部),并且使用相同的 hash 算法。
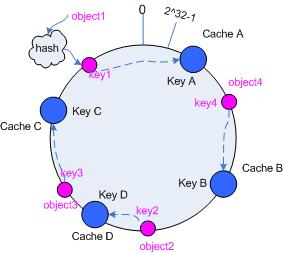
假设当前有 A、B 和 C 共 3 台服务器(如下图中蓝色圆圈所示的Cache A,Cache B,Cache C),那么其映射结果将如图所示,它们在hash空间中,以对应的 hash 值排列。
步骤四:把对象映射到服务器(这一步是核心,实现对象和服务器的映射关系)
现在 cache 和对象都已经通过
同一个 hash 算法映射到环形 hash数值空间中了,接下来要考虑的就是如何将对象映射到 cache 上面。在这个环形空间中,如果沿着
顺时针方向从对象的 key 值出发,直到遇见一个服务器, 那么就将该对象存储在这个服务器上。因为对象和服务器的 hash 值是固定的,因此这个服务器必然是唯一和确定的。这样找到了对象和服务器的映射方法。那么根据上面的方法,对象 object1 将被存储到服务器 A 上,object2 和 object3 对应到服务器 C,object4 对应到服务器 B。如上图所示,带箭头的虚线表示映射关系。
步骤五:考察服务器的变动
前面讲过,通过 hash 算法然后求余的方法带来的最大问题就在于不能满足单调性,当服务器有所变动时,服务器会失效,进而对后台服务器造成巨大的冲击,现在就来分析Consistent Hashing 算法的单调性。
(1) 移除服务器。
考虑假设服务器 B 挂掉了,根据上面讲到的映射方法,这时受影响的将只是那些沿cache B 逆时针遍历直到下一个服务器(服务器 C )之间的对象,也即是本来映射到服务器 B上的那些对象。
因此这里仅需要变动对象 object4,将其重新映射到服务器 C 上即可,如下图所示。
(2) 添加服务器。
再考虑添加一台新的服务器 D 的情况,假设在这个环形 hash 空间中,服务器 D 被映射在对象 object2 和 object3 之间。这时受影响的仅是那些沿 cache D 逆时针遍历直到下一个服务器(服务器 B )之间的对象,将这些对象重新映射到服务器 D 上即可。 因此这里仅需要变动对象 object2,将其重新映射到服务器 D 上,如下图所示。
考量 hash 算法的另一个指标是
平衡性(Balance),定义:平衡性是指哈希的结果能够尽可能分布到所有的缓冲中,这样可以使所有的缓冲空间都得到利用。hash 算法并不能保证绝对的平衡,如果服务器较少,对象并不能被均匀地映射到服务器上,比如在上面的例子中,仅部署服务器 A 和服务器 C 的情况下,在 4 个对象中, 服务器 A 仅存储了 object1,而服务器 C 则存储了 object2、object3 和 object4,分布是很不均衡的。
为了解决这种情况,Consistent Hashing 引入了“虚拟节点”的概念,它可以如下定义:“虚拟节点”( virtual node )是实际节点在 hash 空间的复制品,一个实际节点对应若干个“虚拟节点”,这个对应个数也称为“复制个数”,“虚拟节点”在 hash 空间中以 hash 值排列。仍以仅部署服务器 A 和 服务器 C 的情况为例。现在我们引入虚拟节点,并设置“复制个数”为 2,这就意味着一共会存在4个“虚拟节点”,服务器 A1 和服务器 A2 代表服务器 A;服务器 C1 和服务器 C2 代表服务器 C,假设一种比较理想的情况如下图所示。
此时,对象到“虚拟节点”的映射关系为:objec1->服务器 A2;objec2->服务器 A1;objec3->服务器 C1;objec4->服务器 C2。
因此对象 object1 和 object2 都被映射到服务器 A 上,而 object3 和 object4 映射到 服务器 C 上,平衡性有了很大提高。引入“虚拟节点”后,映射关系就从 { 对象 -> 节点 } 转换到了 { 对象 -> 虚拟节点 ->节点} 。
自此,一致性哈希算法的主要精髓就介绍完毕了,要想理解该算法,必然得亲自动手实现一个才能掌握。下面我们来实现一下Consistent Hashing算法。
二、实现一个简单的一致性哈希算法
1、在写Consistent Hashing算法之前,我们要先写一个对象和服务器共用的哈希函数,该哈希函数可以使对象和服务器都映射到同一hash数值空间区域。该hash算法我们用MD5压缩算法来实现。代码如下,关键地方参考注释:
package webspider.consistenthash;
import java.security.MessageDigest;
import java.security.NoSuchAlgorithmException;
/**
* hash函数,根据key生成hash
*
* @author typ
*
*/
public class HashFunction {
/**
* 用MD5压缩算法,生成hashmap的key值
*
* @param source
* @return
* @throws NoSuchAlgorithmException
*/
public String hash(String key) {
String s = null;
MessageDigest md;
try {
md = MessageDigest.getInstance("MD5");
md.update(key.getBytes());
// MD5的结果:128位的长整数,存放到tmp中
byte tmp[] = md.digest();
s = toHex(tmp);
} catch (NoSuchAlgorithmException e) {
e.printStackTrace();
}
return s;
}
/**
* 将二进制的长整数转换为16进制的数字,以字符串表示
*
* @param bytes
* @return
*/
public String toHex(byte[] bytes) {
// hexDigits的用处是:将任意字节转换为十六进制的数字
char hexDigits[] = "0123456789abcdef".toCharArray();
// MD5的结果:128位的长整数,用字节表示就是16个字节,用十六进制表示的话,使用两个字符,所以表示成十六进制需要32个字符
char str[] = new char[16 * 2];
int k = 0;
for (int i = 0; i < 16; i++) {
byte b = bytes[i];
// 逻辑右移4位,与0xf(00001111)相与,为高四位的值,然后再hexDigits数组中找到对应的16进制值
str[k++] = hexDigits[b >>> 4 & 0xf];
// 与0xf(00001111)相与,为低四位的值,然后再hexDigits数组中找到对应的16进制值
str[k++] = hexDigits[b & 0xf];
}
String s = new String(str);
return s;
}
}
2、有了hash算法,我们来写实现环形hash空间的Consistent Hashing算法,如下所示,关键地方参考注释:(核心地方就是get方法,看是如何实现一个逻辑的环形hash空间的)
package webspider.consistenthash;
import java.util.Collection;
import java.util.HashSet;
import java.util.SortedMap;
import java.util.TreeMap;
/**
* 利用一致性hash,计算得到对象要存放的服务器
*
* @author typ
*
* @param <T>
*/
public class ConsistentHash<T> {
// 哈希函数类,这个类由自己定义,可以用MD5压缩法
private final HashFunction hashFunction;
// 虚拟节点个数
private final int numberOfReplicas;
// 建立有序的map
private final SortedMap<String, T> circle = new TreeMap<String, T>();
public ConsistentHash(HashFunction hashFunction, int numberOfReplicas,
Collection<T> nodes) {
this.hashFunction = hashFunction;
this.numberOfReplicas = numberOfReplicas;
for (T node : nodes) {
add(node);
}
}
/**
* map中添加服务器节点
*
* @param node
*/
public void add(T node) {
String key;
// 虚拟节点所在的hash处,存放对应的实际的节点服务器
for (int i = 0; i < numberOfReplicas; i++) {
key = node.toString() + i;
circle.put(hashFunction.hash(key), node);
}
}
/**
* map中移除服务器节点
*
* @param node
*/
public void remove(T node) {
String key;
for (int i = 0; i < numberOfReplicas; i++) {
key = node.toString() + i;
circle.remove(hashFunction.hash(key));
}
}
/**
* 根据对象的key值,映射到hash表中,得到与对象hash值最近的服务器,就是对象待存放的服务器
*
* @param key
* @return
*/
public T get(Object key) {
if (circle.isEmpty()) {
return null;
}
// 得到对象的hash值,根据该hash值找hash值最接近的服务器
String hash = hashFunction.hash((String) key);
// 以下为核心部分,寻找与上面hash最近的hash指向的服务器
// 如果hash表circle中没有该hash值
if (!circle.containsKey(hash)) {
// tailMap为大于该hash值的circle的部分
SortedMap<String, T> tailMap = circle.tailMap(hash);
// tailMap.isEmpty()表示没有大于该hash的hash值
// 如果没有大于该hash的hash值,那么从circle头开始找第一个;如果有大于该hash值得hash,那么就是第一个大于该hash值的hash为服务器
// 既逻辑上构成一个环,如果达到最后,则从头开始
hash = tailMap.isEmpty() ? circle.firstKey() : tailMap.firstKey();
}
return circle.get(hash);
}
/**
* 测试
*
* @param args
*/
public static void main(String[] args) {
// 定义几个服务器的名称,存放到集合中
Collection<String> nodes = new HashSet<String>();
nodes.add("192.0.0.1");
nodes.add("192.0.0.2");
nodes.add("192.0.0.3");
nodes.add("192.0.0.4");
nodes.add("192.0.0.5");
nodes.add("192.0.0.6");
// MD5压缩算法实现的hash函数
HashFunction hashFunction = new HashFunction();
ConsistentHash<String> cHash = new ConsistentHash<String>(hashFunction,
4, nodes);
// 对象的key值为"google_baidu"
String key[] = { "google", "163", "baidu", "sina" };
// 利用一致性哈希,得到该对象应该存放的服务器
String server[] = new String[key.length];
for (int i = 0; i < key.length; i++) {
server[i] = cHash.get(key[i]);
System.out.println("对象 " + key[i] + " 存放于服务器: " + server[i]);
}
}
}
输出结果如下:
对象 google 存放于服务器: 192.0.0.1
对象 163 存放于服务器: 192.0.0.3
对象 baidu 存放于服务器: 192.0.0.5
对象 sina 存放于服务器: 192.0.0.4