ZJU Valid Pattern Lock 解题报告

Valid Pattern Lock
Time Limit: 2 Seconds Memory Limit: 6553

6 KB
Pattern lock security is generally used in Android handsets instead of a password. The pattern lock can be set by joining points on a 3 × 3 matrix in a chosen order. The points of the matrix are registered in a numbered order starting with 1 in the upper left corner and ending with 9 in the bottom right corner.

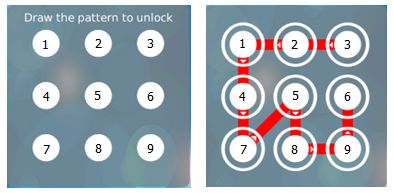
valid_pattern_lock
A valid pattern has the following properties:

A pattern can be represented using the sequence of points which it’s touching for the first time (in the same order of drawing the pattern). And we call those points as active points.
For every two consecutive points A and B in the pattern representation, if the line segment connecting A and B passes through some other points, these points must be in the sequence also and comes before A and B, otherwise the pattern will be invalid.
In the pattern representation we don’t mention the same point more than once, even if the pattern will touch this point again through another valid segment, and each segment in the pattern must be going from a point to another point which the pattern didn’t touch before and it might go through some points which already appeared in the pattern.
Now you are given n active points, you need to find the number of valid pattern locks formed from those active points.

Input

There are multiple test cases. The first line of input contains an integer T indicating the number of test cases. For each test case:

The first line contains an integer n (3 ≤ n ≤ 9), indicating the number of active points. The second line contains n distinct integers a1, a2, … an (1 ≤ ai ≤ 9) which denotes the identifier of the active points.

Output

For each test case, print a line containing an integer m, indicating the number of valid pattern lock.

In the next m lines, each contains n integers, indicating an valid pattern lock sequence. The m sequences should be listed in lexicographical order.

Sample Input

1
3
1 2 3
Sample Output

4
1 2 3
2 1 3
2 3 1
3 2 1

手机的图案解锁，按照题目中给出的要求，任何两个点a，b可以连接为a->b的条件可以描述为：
1.这两个点是处于激活状态的，并且b未被使用过，并且a，b之间没有其他的点。a作为起点，已经被标记过了
2.这两个点是处于激活状态的，并且b未被使用过，并且a，b之间存在一个点c，c点必须是被激活的并且已经被使用的

按照这两个条件，容易想到通过dfs来搜索所有可能的序列，首先要做一个初始化工作，就是记录任意两个点之间的状态，并且在输入的时候，进一步对每个点的状态进行标记，搜索的时候，分别以每个点为起点搜索，找到合法的串的条件就是当串的长度达到所给的激活的点的数量，需要注意的就是，题目并没有说明给出的点的顺序一定是按照数字序的，但是他要求输出是按照数字序的，所以需要事先对给出的序列排序，这样在搜索的时候就能得到按照数字序列排布的结果，因为要输出结果的数量，就需要将结果实现保存，这里用了vector。

#include <iostream>
#include <cmath>
#include <stdio.h>
#include <string>
#include <cstring>
#include <map>
#include <set>
#include <vector>
#include <stack>
#include <queue>
#include <iomanip>
#include <algorithm>
#include <memory.h>
using namespace std;

int cross[10][10];//记录任意两个点之间是否有其他点
int visited[10];//-1表示点未激活，0表示激活了但已经使用，1表示激活了并且未使用
int cas,len;
vector<string> result;//用vector记录每一种结果
int n=0;
int active[9];
void init()//初始化
{
    memset(cross,0,sizeof(cross));
    cross[1][7]=4;
    cross[1][3]=2;
    cross[1][9]=5;
    cross[2][8]=5;
    cross[3][1]=2;
    cross[3][7]=5;
    cross[3][9]=6;
    cross[4][6]=5;
    cross[6][4]=5;
    cross[7][1]=4;
    cross[7][3]=5;
    cross[7][9]=8;
    cross[8][2]=5;
    cross[9][7]=8;
    cross[9][1]=5;
    cross[9][3]=6;
}


void dfs(int num,string path,int count)
{
    int i;

    //cout<<++n<<' '<<path<<' '<<count<<endl;
    if(count==len-1)
    {
        cas++;
        result.push_back(path);
        return;
    }

    for(i=0; i<len; i++)
    {
        if(visited[active[i]]==1)//如果下一个点是已经激活的并且未使用的，才有可能连接
        {
            if(cross[num][active[i]]==0)//如果起点和终点之间没有其他的点，那么这两个点之间必然可以连接
            {
                string path_t;
                path_t=path+(char)('0'+active[i]);
                visited[active[i]]=0;
                dfs(active[i],path_t,count+1);
               // path.erase(path.end()-1);
                visited[active[i]]=1;//回溯
            }
            else//如果起点和终点之间有其他的点
            {
                if(visited[cross[num][active[i]]]==0)//并且这个点是已激活的，已使用的，也是可以连接的
                {
                    string path_t;
                    path_t=path+(char)('0'+active[i]);
                    visited[active[i]]=0;
                    dfs(active[i],path_t,count+1);
                   // path.erase(path.end()-1);
                    visited[active[i]]=1;//回溯
                }
            }
        }

    }
}

int main()
{
    int T,i,j;

    scanf("%d",&T);
    init();
    while(T--)
    {
        cas=0;
        result.clear();
        memset(visited,-1,sizeof(visited));
        scanf("%d",&len);
        for(i=0; i<len; i++)
        {
            scanf("%d",&active[i]);
            visited[active[i]]=1;
        }
        sort(active,active+len);//因为题目给出的点不一定是按照顺序的，所以要先排序，然后得到的结果就是数字序的
        for(i=0; i<len; i++)
        {
            //for(j=0; j<len; j++)
               // visited[active[j]]=1;
            string path;
            path+=(char)('0'+active[i]);
            visited[active[i]]=0;
            dfs(active[i],path,0);
            visited[active[i]]=1;
            path.erase();
        }
        printf("%d\n",cas);
        for(i=0; i<cas; i++)
        {
            for(j=0; j<len; j++)
            {
                printf("%c",result[i][j]);
                if(j<len-1)
                    printf(" ");
            }
            printf("\n");
        }
    }
    return 0;
}