程序员编程技术学习笔记——字符串包含
程序员编程技术学习笔记——字符串包含
1.题目描述
给定两个分别由字母组成的字符串A和字符串B,字符串B的长度比字符串A短。请问,如何最快地判断字符串B中所有字母是否都在字符串A里?为了简单起见,我们规定输入的字符串只包含大写英文字母,请实现函数boolStringContains(string &A, string &B)
比如,如果是下面两个字符串:
String 1:ABCD
String 2:BAD
答案是true,即String2里的字母在String1里也都有,或者说String2是String1的真子集。
如果是下面两个字符串:
String 1:ABCD
String 2:BCE
答案是false,因为字符串String2里的E字母不在字符串String1里。
同时,如果string1:ABCD,string 2:AA,同样返回true。
2.解法1:暴力搜索
这个方法简单粗暴好想。假设两个字符串分别是str1和str2. 我们让str2中的每个字符都在str1中搜索,如果有,继续str2中的下一个字符;如果没有直接返回false。这个过程额可以用下面图示来表示:
假设str1.length()=n,str2.length()=m,则这种方法的时间复杂度为O(m*n),空间复杂度为O(1)。时间太长。
实现代码如下:
#include <iostream>
using namespace std;
bool StringContain(string &str1, string &str2)
{
int n=str1.length();
int m=str2.length();
int i, j;
for(i=0; i<m; i++)
{
for(j=0; (j<n) && (str2[i]!=str1[j]); j++); //注意判断条件
if(j==n)
return false;
}
return true;
}
int main()
{
string str1="ABCDE";
string str2="CDE";
bool flag;
flag=StringContain (str1, str2);
cout<<flag<<endl;
return 0;
}
3.解法2:先排序再暴力搜索
这种方法比上一次稍微文雅一些,文雅在没有一股脑的直接搜索,而是先把str1和str2排序,然后再那str2中的每个字符在str1中搜索。这里搜索也有讲究,不是说每次都是从头再来搜索,而是两个字符串同时前进。判断当前的str1字符和str2字符的大小,如果小,则str1的指针后移一个,继续判断。如果这个时候相等,则str2后移;否则,直接false。这点在编程中一定要注意。这种思路的时间复杂度为O(mlogm+nlogn+m+n)我们先用下图给出该种解法的思想,然后再编程实现:
bool StringContain(string &str1,string &str2)
{
int n=str1.length();
int m=str2.length();
qsort(str1, n, sizeof(char), cmp);
qsort(str2, m, sizeof(char), cmp);
for (int p1 = 0, p2 = 0; p2 < m;)
{
while ((p1 < n) && (str1[p1] < str2[p2]))
{
++p1;
}
if ((p1 >= str1.length()) || (str1[p1] > str2[p2]))
{
return false;
}
++p2;
}
return true;
}
4.解法3:基于HashTable
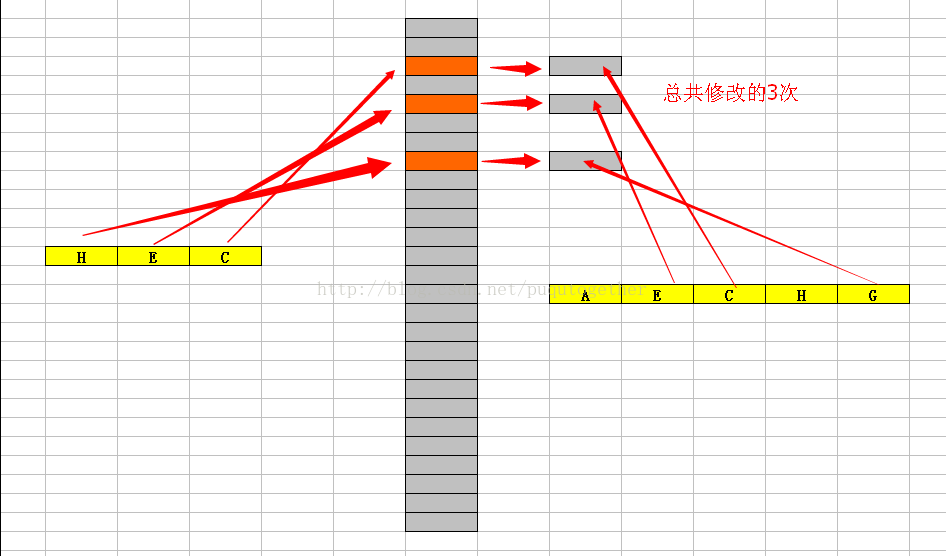
这种方法使用的思想是基于hashtable.我们先用一个26长的数组,每个都是0.然后看str2中出现的字符就把数组中对应位置设为1.遍历一次str1,如果str1的字符在数组中为0,则不处理;如果为1,则修改为0.最后看修改的次数是否为str2的串长m,如果是,返回true;否则,为false。该解法的时间复杂度为O(m+n), 空间复杂度为O(m).
我们用下图来形象说明:
bool StringContain(string &str1, string &str2)
{
int n=str1.length();
int m=str2.length();
int *table=new int[m];
memset(table, 0, m);
for(int i=0; i<m; i++)
{
table[str2[i]-'A']=1;
}
int count=0;
for(int j=0; j<n; j++)
{
int index=str1[j]-'A';
if(table[index]==1)
{
count++;
table[index]=0;
}
}
if(count==m)
return true;
else
return false;
}
july的博客中用移位来写的,一样的道理。还是觉得这样写好理解一点。
5. 解法4:素数法
这种方法巧妙运用了素数的特性。假设有一个仅由字母组成字串,让每个字母与一个素数对应,从2开始,往后类推,A对应2,B对应3,C对应5,......。遍历第一个字串,把每个字母对应素数相乘。最终会得到一个整数。
利用上面字母和素数的对应关系,对应第二个字符串中的字母,然后轮询,用每个字母对应的素数除前面得到的整数。如果结果有余数,说明结果为false。如果整个过程中没有余数,则说明第二个字符串是第一个的子集了(判断是不是真子集,可以比较两个字符串对应的素数乘积,若相等则不是真子集)。
思路总结如下:
按照从小到大的顺序,用26个素数分别与字符'A'到'Z'一一对应。
遍历长字符串,求得每个字符对应素数的乘积。
遍历短字符串,判断乘积能否被短字符串中的字符对应的素数整除。
输出结果。
这种方法的时间复杂度为O(m+n),空间复杂度为O(1)。
但是,当字符串的长度很长时,乘积就会很大,可能要涉及到大数乘除运算了。不过,个人觉得这种方法特别能够体现:好的算法都是和题目紧密结合的,这样的思想。
代码如下:
bool StringContain(string &str1, string &str2)
{
int n=str1.length();
int m=str2.length();
int prime[26]={2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59,61, 67, 71, 73, 79, 83, 89, 97, 101};
int prod=1;
for(int i=0; i<n; i++)
{
int x=prime[str1[i]-'A'];
if(prod%x)
prod*=x;
}
for(int j=0; j<m; j++)
{
int y=prime[str2[j]-'A'];
if(prod%y!=0)
return false;
}
return true;
}
6. 举一反三
变位词:如果两个字符串的字符一样,但是顺序不一样,被认为是兄弟字符串,比如bad和adb即为兄弟字符串,现提供一个字符串,如何在字典中迅速找到它的兄弟字符串,请描述数据结构和查询过程。