Codeforces 514E. Darth Vader and Tree DP+矩阵快速幂
DP处理出前100的值,然后用矩阵快速幂递推剩下的值.
矩阵A: 矩阵B:
相乘之后--->得到了dp4
When Darth Vader gets bored, he sits down on the sofa, closes his eyes and thinks of an infinite rooted tree where each node has exactlyn sons, at that for each node, the distance between it an its i-th left child equals to di. The Sith Lord loves counting the number of nodes in the tree that are at a distance at most x from the root. The distance is the sum of the lengths of edges on the path between nodes.
But he has got used to this activity and even grew bored of it. 'Why does he do that, then?' — you may ask. It's just that he feels superior knowing that only he can solve this problem.
Do you want to challenge Darth Vader himself? Count the required number of nodes. As the answer can be rather large, find it modulo 109 + 7.
The first line contains two space-separated integers n and x (1 ≤ n ≤ 105, 0 ≤ x ≤ 109) — the number of children of each node and the distance from the root within the range of which you need to count the nodes.
The next line contains n space-separated integers di (1 ≤ di ≤ 100) — the length of the edge that connects each node with its i-th child.
Print a single number — the number of vertexes in the tree at distance from the root equal to at most x.
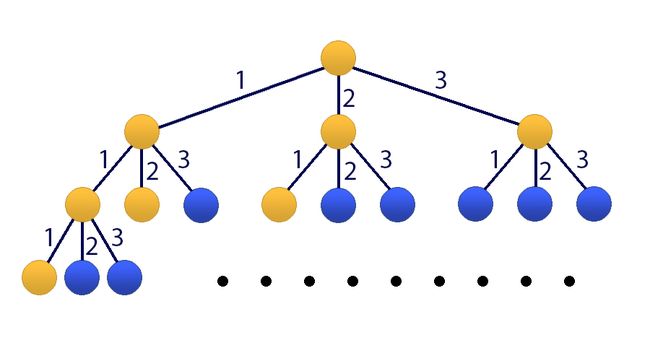
3 3 1 2 3
8
Pictures to the sample (the yellow color marks the nodes the distance to which is at most three)
/**
* Created by ckboss on 15-4-2.
*/
import java.util.*;
public class CF514E {
final int maxn = 100100;
final long mod = 1000000007L;
int n,x;
int[] dist = new int[maxn];
int[] cnt = new int[maxn];
long[] dp = new long[110];
class Matrix{
int nx,ny; long[][] m;
Matrix(){
nx=102;ny=102;m=new long[nx][ny];
}
void initE(){
for(int i=0;i<nx;i++) m[i][i]=1L;
}
void showM(int x,int y){
System.out.println(" let's show it ");
for(int i=0;i<x;i++)
for(int j=0;j<y;j++)
System.out.printf("%d%c",m[i][j],(j==y-1)?'\n':' ');
}
}
Matrix Mult(Matrix a,Matrix b){
Matrix ret = new Matrix();
int nx=a.nx; int ny = b.ny;
for(int i=0;i<nx;i++)
for(int j=0;j<ny;j++)
for(int k=0;k<nx;k++)
ret.m[i][j]=(ret.m[i][j]+(a.m[i][k]*b.m[k][j])%mod)%mod;
return ret;
}
Matrix QuickPow(Matrix M,int n){
Matrix E = new Matrix();
E.initE();
while(n!=0) {
if((n&1)!=0){
E = Mult(E,M);
}
M = Mult(M,M);
n/=2;
}
return E;
}
Matrix gouzhao() {
Matrix ret = new Matrix();
for(int i=0;i<=99;i++){
ret.m[i][99]=ret.m[i][100]=cnt[100-i];
if(i>=1) ret.m[i][i-1]=1;
}
ret.m[100][100]=1;
return ret;
}
CF514E(){
Scanner in = new Scanner(System.in);
n=in.nextInt(); x=in.nextInt();
for(int i=0;i<n;i++){
dist[i]=in.nextInt();
cnt[dist[i]]++;
}
dp[0]=1;
for(int i=1;i<=100;i++) {
for(int j=1;j<=i;j++) {
dp[i]=(dp[i]+cnt[j]*dp[i-j]%mod)%mod;
}
}
long ans=0;
if(x<=100){
for(int i=0;i<=x;i++) ans=(ans+dp[i])%mod;
}
else{
Matrix MX = gouzhao();
MX = QuickPow(MX,x-100);
long sum=0;
for(int i=0;i<=100;i++){
sum=(sum+dp[i])%mod;
}
for(int i=0;i<=99;i++){
ans=(ans+dp[i+1]*MX.m[i][100]%mod)%mod;
}
ans=(ans+sum*MX.m[100][100])%mod;
}
System.out.println(ans);
}
public static void main(String[] agrs) {
new CF514E();
}
}


