Project Euler Problem 91-100
Problem 91 Right triangles with integer coordinates
格点直角三角形
点P(x1, y1)和点Q(x2, y2)都是格点,并与原点O(0,0)构成ΔOPQ。
点P(x1, y1)和点Q(x2, y2)都是格点,并与原点O(0,0)构成ΔOPQ。
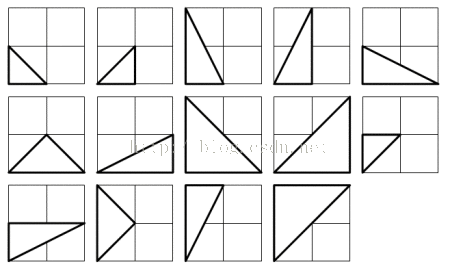
当点P和点Q的所有坐标都在0到2之间,也就是说0 ≤ x1, y1, x2, y2 ≤ 2时,恰好能构造出14个直角三角形。
如果0 ≤ x1, y1, x2, y2 ≤ 50,能构造出多少个直角三角形?
数据规模不大,直接枚举即可
#include<iostream>
using namespace std;
bool inline CHECK(int a,int b,int c,int d)
{
int x=a*a+b*b,y=c*c+d*d,z=(a-c)*(a-c)+(b-d)*(b-d);
return x+y==z||z+y==x||x+z==y;
}
const int limit=50;
int main()
{
int ans=0;
for(int x1=0;x1<=limit;++x1)
for(int y1=0;y1<=limit;y1++)
for(int x2=0;x2<=limit;++x2)
for(int y2=0;y2<=limit;y2++)
if(x1+y1!=0 && x2+y2!=0&& y2*x1!=x2*y1&&CHECK(x1,y1,x2,y2))
ans++;
cout<<ans/2<<endl;/*** divided by 2 is necessary ***/
return 0;
}
Problem 92 Square digit chains
平方数字链将一个数的所有数字的平方相加得到一个新的数,不断重复直到新的数已经出现过为止,这构成了一条数字链。
例如,
44 → 32 → 13 → 10 → 1 → 1
85 → 89 → 145 → 42 → 20 → 4 → 16 → 37 → 58 → 89
可见,任何一个到达1或89的数字链都会陷入无尽的循环。更令人惊奇的是,从任意数开始,最终都会到达1或89。
有多少个小于一千万的数最终会到达89?
暴力继续
#include<iostream>
using namespace std;
const int limit=10000001;
bool have[limit]={0};// true for 89
int tmp[500],cnt,sum;
int square[]={0,1,4,9,16,25,36,49,64,81};
inline bool calcu(int n)
{
cnt=0;
if(have[n]) return true;
while(!have[n])
{
if(n==1) return false;
tmp[cnt++]=n;
sum=0;
while(n)
{
sum+=square[n%10];
n/=10;
}
n=sum;
}
if(tmp[0]>1000) return true;
for(int i=0;i<cnt;i++)
have[tmp[i]]=true;
return true;
}
int main()
{
have[89]=true;
int ans=0;
for(int i=1;i<limit;i++)
if(calcu(i)) ans++;
cout<<ans<<endl;
return 0;
}
Problem 93 Arithmetic expressions
算术表达式
使用集合{1, 2, 3, 4}中每个数字恰好一次以及(+, −, *, /)四则运算和括号,可以得到不同的正整数。
例如,
8 = (4 * (1 + 3)) / 2
14 = 4 * (3 + 1 / 2)
19 = 4 * (2 + 3) − 1
36 = 3 * 4 * (2 + 1)
注意不允许直接把数字连起来,如12 + 34。
使用集合{1, 2, 3, 4},可以得到31个不同的数,其中最大值是36,以及1到28之间所有的数。
若使用包含有四个不同数字a < b < c < d的集合可以得到从1到n之间所有的数,求其中使得n最大的集合,并将你的答案写成字符串:abcd。
使用集合{1, 2, 3, 4}中每个数字恰好一次以及(+, −, *, /)四则运算和括号,可以得到不同的正整数。
例如,
8 = (4 * (1 + 3)) / 2
14 = 4 * (3 + 1 / 2)
19 = 4 * (2 + 3) − 1
36 = 3 * 4 * (2 + 1)
注意不允许直接把数字连起来,如12 + 34。
使用集合{1, 2, 3, 4},可以得到31个不同的数,其中最大值是36,以及1到28之间所有的数。
若使用包含有四个不同数字a < b < c < d的集合可以得到从1到n之间所有的数,求其中使得n最大的集合,并将你的答案写成字符串:abcd。
还是暴力题
#include<set>
#include<iostream>
#include<algorithm>
#define eps 0.0000000001
using namespace std;
int a,b,c,d,tmp;
set<int> st;
inline double operate(double a,double b,int opt) //opt 0~3 +-*/
{
if(opt<2)//binary search, 2 comparsions on average,use case-switch or if-else 2.5 on average
return opt==0?a+b:a-b;
return opt==2?a*b:a/b;
}
void calcu(int n)
{
int opt1=n&3,opt2=(n&12)>>2,opt3=(n&48)>>4;
double ans[5];
ans[0]=operate(operate(a,b,opt1),operate(c,d,opt3),opt2);
ans[1]=operate(operate(operate(a,b,opt1),c,opt2),d,opt3);
ans[2]=operate(operate(a,operate(b,c,opt2),opt1),d,opt3);
ans[3]=operate(a,operate(operate(b,c,opt2),d,opt3),opt1);
ans[4]=operate(a,operate(b,operate(c,d,opt3),opt2),opt1);
for(int i=0; i<5; i++)
{
tmp=ans[i]+eps;
if(tmp>0&& tmp-ans[i] < eps && tmp -ans[i]> -eps)
st.insert(tmp);
}
}
int main()
{
int num[4],len=0,ans;
for(int i=1; i<7; i++)
for(int j=i+1; j<8; j++)
for(int k=j+1; k<9; k++)
for(int h=k+1; h<10; h++)
{
num[0]=i,num[1]=j,num[2]=k,num[3]=h;
st.clear();
for(int f=0; f<24; f++)//24=4!
{
a=num[0],b=num[1],c=num[2],d=num[3];
for(int g=0;g<64;g++)//64=4*4*4
calcu(g);
next_permutation(num,num+4);
}
tmp=0;
for(set<int> ::const_iterator it=st.begin(); it!=st.end(); ++it)
if(*it!=++tmp) break;
if(tmp-1>len)
{
len=tmp-1;
ans=i*1000+j*100+k*10+h;
}
}
cout<<len<<" "<<ans<<endl;
return 0;
}
/**a b c d
((a b) (c d))
(((a b) c) d)
((a(b c))d)
(a((b c)d))
(a(b(c d)))
***/
//24*64*5*C9,4
Problem 94 Almost equilateral triangles
几乎等边的三角形可以证明,不存在边长为整数的等边三角形其面积也是整数。但是,存在几乎等边的三角形 5-5-6,其面积恰好为12。
我们定义几乎等边的三角形是有两条边一样长,且第三边与这两边最多相差1的三角形。
对于所有边长和面积均为整数且周长不超过十亿(1,000,000,000)的三角形,求其中几乎等边的三角形的周长之和。
直接暴力,比较慢128s
#include<iostream>
#include<math.h>
#include<stdio.h>
#include<time.h>
using namespace std;
#define eps 0.000001
const long long limit=1e9;
long long ans=0;
int main()
{
int start=clock();
freopen("out.txt","w",stdout);
for(long long b,h,tmp, a=2;a<=limit/3;a++)
{
b=a-1;
tmp=4*a*a-b*b;
h=sqrt(tmp)+eps;
if(h*h==tmp&&(h*b)%8==0)
ans+=a+a+b;
b=a+1;
tmp=4*a*a-b*b;
h=sqrt(tmp)+eps;
if(h*h==tmp&&(h*b)%8==0)
ans+=a+a+b;
}
cout<<ans<<endl;
cout<<"time : "<<clock()-start<<endl;
return 0;
}
/***
518408346
128s
a a b
b*(4*a*a +b*b)^0.5/4
***/
Problem 95 Amicable chains
亲和数链
一个数除了本身之外的因数称为真因数。例如,28的真因数是1、2、4、7和14。这些真因数的和恰好为28,因此我们称28是完全数。
有趣的是,220的真因数之和是284,同时284的真因数之和是220,构成了一个长度为2的链,我们也称之为亲和数对。
有一些更长的序列并不太为人所知。例如,从12496出发,可以构成一个长度为5的链:
12496 → 14288 → 15472 → 14536 → 14264 (→ 12496 → …)
由于这条链最后又回到了起点,我们称之为亲和数链。
找出所有元素都不超过一百万的亲和数链中最长的那条,并给出其中最小的那个数。
直接暴力,8s
#include<iostream>
using namespace std;
const int limit=1000000;
bool have[limit+1]= {0};
int len=0,ans;
int amicable[limit+1];
int main()
{
for(int j,i=1; i<=limit; i++)
{
amicable[i]=1;
for(j=2; j*j<i; j++)
if(i%j==0)
amicable[i]+=(j+i/j);
if(j*j==i)
amicable[i]+=j;
if(amicable[i]>limit)
amicable[i]=0;
}
for(int i=1; i<=limit; i++)
{
int nxt=i,cnt=0;
while(amicable[nxt]&&!have[nxt])
{
have[nxt]=true;
nxt=amicable[nxt];
++cnt;
if(nxt==i)
{
if(len<cnt)
{
len=cnt;
ans=i;
}
break;
}
}
nxt=i;
while(cnt)
{
have[nxt]=false;
nxt=amicable[nxt];
--cnt;
}
}
cout<<ans<<" "<<len<<endl;
return 0;
}
Problem 96 Su Doku
数独
数独(日语原意为数的位置)是一种热门的谜题。它的起源已不可考,但是与欧拉发明的一种类似而更加困难的谜题拉丁方阵之间有着千丝万缕的联系。数独的目标是替换掉9乘9网格中的空白位置(或0),使得每行、每列以及每个九宫格中恰好都包含数字1~9。如下是一个典型的数独谜题以及它的解答。
0 0 3 0 2 0 6 0 0 * 4 8 3 9 6 7 2 5 1
9 0 0 3 0 5 0 0 1 * 9 2 1 3 4 5 8 7 6
0 0 1 8 0 6 4 0 0 * 6 5 7 8 2 1 4 9 3
0 0 8 1 0 2 9 0 0 * 5 4 8 7 2 9 1 3 6
7 0 0 0 0 0 0 0 8 * 1 3 2 5 6 4 7 9 8
0 0 6 7 0 8 2 0 0 * 9 7 6 1 3 8 2 4 5
0 0 2 6 0 9 5 0 0 * 3 7 2 8 1 4 6 9 5
8 0 0 2 0 3 0 0 9 * 6 8 9 2 5 3 4 1 7
0 0 5 0 1 0 3 0 0 * 5 1 4 7 6 9 3 8 2
一个构造精良的数独谜题应该包含有唯一解,且能够通过逻辑推断来解决,尽管有时可能必须通过“猜测并检验”来排除一些选项(这一要求目前还颇受争议)。寻找答案的复杂度决定了题目的难度;上面这个谜题被认为是简单的谜题,因为我们可以通过直截了当的演绎推理来解决它。
在这个6K的文本文件sudoku.txt(右击并选择“目标另存为……”)中包含有50个不同难度的数独谜题,但保证它们都只有唯一解(文件中的第一个谜题就是上述样例)。
解开这50个谜题,找出每个谜题解答左上角的三个数字并连接起来,给出这些数的和;举例来说,上述样例解答左上角的三个数字连接起来构成的数是483。
0 0 3 0 2 0 6 0 0 * 4 8 3 9 6 7 2 5 1
9 0 0 3 0 5 0 0 1 * 9 2 1 3 4 5 8 7 6
0 0 1 8 0 6 4 0 0 * 6 5 7 8 2 1 4 9 3
0 0 8 1 0 2 9 0 0 * 5 4 8 7 2 9 1 3 6
7 0 0 0 0 0 0 0 8 * 1 3 2 5 6 4 7 9 8
0 0 6 7 0 8 2 0 0 * 9 7 6 1 3 8 2 4 5
0 0 2 6 0 9 5 0 0 * 3 7 2 8 1 4 6 9 5
8 0 0 2 0 3 0 0 9 * 6 8 9 2 5 3 4 1 7
0 0 5 0 1 0 3 0 0 * 5 1 4 7 6 9 3 8 2
一个构造精良的数独谜题应该包含有唯一解,且能够通过逻辑推断来解决,尽管有时可能必须通过“猜测并检验”来排除一些选项(这一要求目前还颇受争议)。寻找答案的复杂度决定了题目的难度;上面这个谜题被认为是简单的谜题,因为我们可以通过直截了当的演绎推理来解决它。
在这个6K的文本文件sudoku.txt(右击并选择“目标另存为……”)中包含有50个不同难度的数独谜题,但保证它们都只有唯一解(文件中的第一个谜题就是上述样例)。
解开这50个谜题,找出每个谜题解答左上角的三个数字并连接起来,给出这些数的和;举例来说,上述样例解答左上角的三个数字连接起来构成的数是483。
用深搜,都不用怎么优化,速度还行
#include<iostream>
#include<algorithm>
#include<stdio.h>
#include<string>
using namespace std;
int data[9][9],tmp,ans=0,cnt;
bool rows[9][10]= {0},cols[9][10]= {0},rc33[3][3][10]= {0},done;
struct May
{
int cnt,may[9],x,y;
May():cnt(0),x(0),y(0) {}
bool operator < (const May & b) const
{
return this->cnt<b.cnt;
}
void add(int i)
{
may[cnt++]=i;
}
void setxy(int _x,int _y)
{
x=_x,y=_y;cnt=0;
}
} maybe[81];
void dfs(int lv=0)
{
if(lv==cnt||done)
{
if(!done)
{
ans+=data[0][0]*100+data[0][1]*10+data[0][2];
for(int i=0; i<9; i++)
{
for(int j=0; j<9; j++)
cout<<data[i][j]<<" ";
cout<<endl;
}
}
done=true;
return ;
}
int x,y,s;
x=maybe[lv].x;
y=maybe[lv].y;
for(int i=maybe[lv].cnt-1; i>=0; i--)
{
s=maybe[lv].may[i];
if(rows[x][s]&&cols[y][s]&&rc33[x/3][y/3][s])
{
rows[x][s]=cols[y][s]=rc33[x/3][y/3][s]=false;
data[x][y]=s;
dfs(lv+1);
rows[x][s]=cols[y][s]=rc33[x/3][y/3][s]=true;
}
}
}
bool read()
{
string str;
if(!(cin>>str)) return false;
cin>>str;
for(int i=0; i<9; i++)//init
for(int j=0; j<10; j++)
rows[i][j]=cols[i][j]=rc33[i/3][i%3][j]=true;
for(int i=0; i<9; i++)
{
cin>>str;
for(int j=0; j<9; j++)
{
int tmp=str[j]-'0';
rows[i][data[i][j]=tmp]=cols[j][tmp]=rc33[i/3][j/3][tmp]=false;
}
}
return true;
}
void deal()
{
cnt=0;
for(int i=0; i<9; i++)
for(int j=0; j<9; j++)
if(!data[i][j])
{
maybe[cnt].setxy(i,j);
for(int k=1; k<10; k++)
if(rows[i][k]&&cols[j][k]&&rc33[i/3][j/3])
maybe[cnt].add(k);
if(maybe[cnt].cnt>0)
++cnt;
}
// sort(maybe,maybe+cnt);// sorting does make it faster but why ?
done=false;// init
dfs();
}
//24702
int main()
{
//freopen("in.txt","r",stdin);
while(read())
deal();
cout<<ans<<endl;
return 0;
}
/**
3 0 0 2 0 0 0 0 0
0 0 0 1 0 7 0 0 0
7 0 6 0 3 0 5 0 0
0 7 0 0 0 9 0 8 0
9 0 0 0 2 0 0 0 4
0 1 0 8 0 0 0 5 0
0 0 9 0 4 0 3 0 1
0 0 0 7 0 2 0 0 0
0 0 0 0 0 8 0 0 6
1231
12
000000000
000000000
000000000
000000000
000000000
000000000
000000000
000000000
000000000
000000000
***/
Problem 97 Large non-Mersenne prime
非梅森大素数
1999年人们发现了第一个超过一百万位的素数,这是一个梅森素数,可以表示为26972593−1,包含有2,098,960位数字。在此之后,更多形如2p−1的梅森素数被发现,其位数也越来越多。
然而,在2004年,人们发现了一个巨大的非梅森素数,包含有2,357,207位数字:28433×2^7830457+1。
找出这个素数的最后十位数字
1999年人们发现了第一个超过一百万位的素数,这是一个梅森素数,可以表示为26972593−1,包含有2,098,960位数字。在此之后,更多形如2p−1的梅森素数被发现,其位数也越来越多。
然而,在2004年,人们发现了一个巨大的非梅森素数,包含有2,357,207位数字:28433×2^7830457+1。
找出这个素数的最后十位数字
使用快速幂,加大数取模就可以了
#include <stdio.h>
#define MOD 10000000000L
long long Multiply(long long a,long long b)
{
const long long mod = 100000;
long long a1 = a/mod;
long long a2 = a%mod;
long long b1 = b/mod;
long long b2 = b%mod;
long long ans = a2*b2;
ans += ((a2*b1)%mod)*mod;
ans %= MOD;
ans += ((b2*a1)%mod)*mod;
ans %= MOD;
return ans;
}
int main()
{
long long ans = 28433,mul = 2;
int power = 7830457;
while(power)
{
if(power&1)
ans = Multiply(ans,mul);
mul = Multiply(mul,mul);
power >>= 1;
}
printf("%lld",++ans);
return 0;
}
Problem 98 Anagramic squares
重排平方数
将单词CARE中的四个字母依次赋值为1、2、9、6,我们得到了一个平方数:1296 = 362。神奇的是,使用同样的数字赋值,重排后的单词RACE同样构成了一个平方数:9216 = 962。我们称CARE和RACE为重排平方单词对,同时规定这样的单词对不允许有前导零或是不同的字母赋相同的值。
在这个16K的文本文件words.txt(右击并选择“目标另存为……”)中包含了将近两千个常见英文单词,找出所有的重排平方单词对(一个回文单词不视为它自己的重排)。
重排平方单词对所给出的最大平方数是多少?
注意:所有的重排单词必须出现在给定的文本文件中。
#include<iostream>
#include<algorithm>
#include<stdio.h>
#include<math.h>
using namespace std;
char chr[20];
struct Word
{
string str,val;
Word(string s="",string v=""):str(s),val(v) {}
bool operator < (Word const & w) const
{
if(this->val!=w.val)
{
if(this->val.length()==w.val.length())
return this->val<w.val;
return this->val.length()>w.val.length();
}
return this->str<w.str;
}
bool operator ==(Word const &w) const
{
return this->val==w.val;
}
void output()
{
cout<<str<<" "<<val<<endl;
}
} words[2000];
int cnt=0;
bool getWord()
{
char tmp=0;
while(tmp!='"'&&tmp!=EOF)
tmp=getchar();
if(tmp==EOF) return false;
int n=0;
do
{
tmp=getchar();
chr[n++]=tmp;
}
while(tmp!='"');
chr[n-1]='\0';
string str(chr);
sort(chr,chr+n-1);
string val(chr);
words[cnt++]=Word(str,val);
return true;
}
int charValue[128]= {0},chars[20],nchar,ans=0, strValue[10],nstr;
string strs[10];
bool used[10]= {0};
void dfs(int lv=0)
{
if(lv==nchar)
{
int nsquare=0;
for(int i=0; i<nstr; i++)
{
if(charValue[int(strs[i][0])]==0)
continue;
strValue[i]=0;
for(int j=0; j<strs[i].length(); j++)
strValue[i]=strValue[i]*10+charValue[int(strs[i][j])];
int tmp=sqrt(strValue[i])+0.5;
if(tmp*tmp==strValue[i])
strValue[nsquare++]=strValue[i];
}
if(nsquare>1)
for(int i=0; i<nsquare; i++)
{
cout<<strValue[i]<<" ";
if(ans<strValue[i])
ans=strValue[i];
}
}
for(int i=0; i<10; i++)
if(!used[i])
{
used[i]=true;
charValue[chars[lv]]=i;
dfs(lv+1);
used[i]=false;
}
}
int main()
{
freopen("p098_words.txt","r",stdin);
while(getWord());///Read all
cout<<cnt<<endl;
sort(words,words+cnt);
int lenstr=0;
for(int i=1; i<cnt; i++)
{
if(words[i-1]==words[i])
{
if(ans!=0&&lenstr>words[i].str.length())
break;
lenstr=words[i].str.length();
nchar=nstr=0;
chars[nchar++]=words[i].val[0];
for(int j=1; j<words[i].val.length(); j++)
if(words[i].val[j]!=words[i].val[j-1])
chars[nchar++]=words[i].val[j];
strs[nstr++]=words[i-1].str;
while(words[i-1]==words[i])
strs[nstr++]=words[i++].str;
for(int i=0; i<10; i++)
used[i]=false;
dfs();
cout<<nstr<<" ";
words[i].output();
}
}
cout<<"Answer : "<<ans<<endl;
return 0;
}
/***
18769
***/
Problem 99 Largest exponential
最大的幂比较两个如211和37这样写成幂的形式的数并不困难,任何计算器都能验证211 = 2048 < 37 = 2187。
然而,想要验证632382518061 > 519432525806就会变得非常困难,因为这两个数都包含有超过三百万位数字。
22K的文本文件base_exp.txt(右击并选择“目标另存为……”)有一千行,每一行有一对底数和指数,找出哪一行给出的幂的值最大。
注意:文件的前两行就是上述两个例子。
直接取对数进行比较就可以了
ary=[ ...] >>> mx=0 >>> a,b,idx=0,0,0 >>> for i in range(1000): tmp=ary[i*2+1]*1.0*math.log(ary[i*2]) if tmp > mx: mx,a,b,idx=tmp,ary[i*2],ary[i*2+1],i+1 >>> idx 709
Problem 100 Arranged probability
安排概率
在一个盒子中装有21个彩色碟子,其中15个是蓝的,6个是红的。如果随机地从盒子中取出两个碟子,取出两个蓝色碟子的概率是P(BB) = (15/21)×(14/20) = 1/2。
下一组使得取出两个蓝色盘子的概率恰好为50%的安排,是在盒子中装有85个蓝色碟子和35个红色碟子。
当盒子中装有超过10^12 = 1,000,000,000,000个碟子时,找出第一组满足上述要求的安排,并求此时盒子中蓝色碟子的数量。
在一个盒子中装有21个彩色碟子,其中15个是蓝的,6个是红的。如果随机地从盒子中取出两个碟子,取出两个蓝色碟子的概率是P(BB) = (15/21)×(14/20) = 1/2。
下一组使得取出两个蓝色盘子的概率恰好为50%的安排,是在盒子中装有85个蓝色碟子和35个红色碟子。
当盒子中装有超过10^12 = 1,000,000,000,000个碟子时,找出第一组满足上述要求的安排,并求此时盒子中蓝色碟子的数量。
这是一个丢番图方程的问题设蓝色球的个数为x个总共有 n个球
则有2(x-1)x = n*(n-1) 通过换元 可以变成 2a*a-b*b = 25 这是典型的佩尔方程的形式可以直接求出公式解,亦可以求出递推解,我用的公式解然后求精得出的答案
import random
x0,y0 = 5,5
r2 = 2**0.5
c1 = (r2*x0+y0)
c2 = (r2*x0-y0)
limit = 10
def Xn(n):
xn = (c1*c1/25.0)**n/c1
xn += (c2*c2/25.0)**n/c2
xn /= r2
xn = xn*12.5
return xn
def Yn(n):
yn = (c1*c1/25.0)**n/c1
yn -= (c2*c2/25.0)**n/c2
yn *= 12.5
return yn
def findAns(x,y):
for i in xrange(0,limit):
if i%2 ==1:
nx = x + (i/2)*5
else:
nx = x - (i/2)*5
for j in xrange(0,limit):
if j%2 == 1:
ny = y + (j/2)*5
else:
ny = y - (j/2)*5
diff = 2*nx*nx -ny*ny
if diff == 25:
tx = nx/10+1
ty = ny/10+1
if tx*(tx-1)*2 == ty*(ty-1) and ty > 10**12:
print 'bule discs',tx,'all discs',ty
return True
break
for i in range(200):
x = Xn(i+1)
y = Yn(i+1)
ix = int(x)
iy = int(y)
#print 2*x*x-y*y ,'###',x,y,'>>>>',2*ix*ix-iy*iy,ix,iy
findAns((ix/10)*10,(iy/10)*10)