Project Euler Problem 81-90

Project Euler Problem 81-90

Project Euler 81-90题解

Problem 81 Path sum: two ways

路径和：两个方向
在如下的5乘5矩阵中，从左上方到右下方始终只向右或向下移动的最小路径和为2427，由标注红色的路径给出。

131 673 234 103 18
201 96 342 965 150
630 803 746 422 111
537 699 497 121 956
805 732 524 37 331
在这个31K的文本文件matrix.txt（右击并选择“目标另存为……”）中包含了一个80乘80的矩阵，求出从该矩阵的左上方到右下方始终只向右和向下移动的最小路径和。

简单的动态规划

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <vector>

using namespace std;

typedef long long LL;
typedef long double LD;

const int MAXN=102;
const int INF= 1e9;

int m,n,T;
int data[MAXN][MAXN],dp[MAXN][MAXN],dpp[MAXN][MAXN];

int getN()
{
    char tmp;
    int n=0;
    do
    {
        tmp=getchar();
        if(tmp>='0'&&tmp<='9')
            n=n*10+int(tmp-'0');
    }while(tmp>='0'&&tmp<='9');
    //cout<<n<<" ";

    return n;
}

int main()
{
    freopen("p81in.txt","r",stdin);
    m=n=80;
    for(int i=0; i<m; i++)
        for(int j=0; j<n; j++)
        {
            //scanf("%d",&data[i][j]);
            data[i][j]=getN();
            dp[i][j]=INF;
        }
    dp[0][0]=dpp[0][0]=data[0][0];       //init
    for(int i=1; i<m; i++) //init
        dp[i][0]=dpp[i][0]=dp[i-1][0]+data[i][0]; //init
    for(int j=1; j<n; j++)
    {
        for(int i=0; i<m; i++) //right
            dp[i][j]=dpp[i][j]=min(dp[i][j-1]+data[i][j],dp[i][j]);
        for(int i=1; i<m; i++) //down
            dp[i][j]=min(dp[i][j],dp[i-1][j]+data[i][j]);
        //for(int i=m-2; i>=0; i--) //up
          // dpp[i][j]=min(dpp[i][j],dpp[i+1][j]+data[i][j]);
        for(int i=0; i<m; i++) //comebine
            dp[i][j]=dpp[i][j]=min(dp[i][j],dpp[i][j]);
    }
    printf("Answer: %d",dp[n-1][n-1]);
    return 0;
}


/** 131 673 234 103 18 201 96 342 965 150 630 803 746 422 111 537 699 497 121 965 805 732 524 37 331 **/

Problem 82 Path sum: three ways

路径和：三个方向

注意：这是第81题的一个更具挑战性的版本。

在如下的5乘5矩阵中，从最左栏任意一格出发，始终只向右、向上或向下移动，到最右栏任意一格结束的最小路径和为994，由标注红色的路径给出。

131 673 234 103 18
201 96 342 965 150
630 803 746 422 111
537 699 497 121 956
805 732 524 37 331

在这个31K的文本文件matrix.txt（右击并选择“目标另存为……”）中包含了一个80乘80的矩阵，求出从最左栏到最右栏的最小路径和。
动态规划

#include <algorithm>
#include <cstdio>
const int MAXN=102;
const int INF= 1e9;
int m,n,ans;
int data[MAXN][MAXN],dp[MAXN][MAXN],dpp[MAXN][MAXN];
int getN()
{
    char tmp;
    int n=0;
    do
    {
        tmp=getchar();
        if(tmp>='0'&&tmp<='9')
            n=n*10+int(tmp-'0');
    }
    while(tmp>='0'&&tmp<='9');
    return n;
}
int main()
{
    freopen("p82in.txt","r",stdin);
    m=n=80;
    ans=INF;
    for(int i=0; i<m; i++)
        for(int j=0; j<n; j++)
        {
            data[i][j]=getN();
            dp[i][j]=INF;
        }
    for(int i=0; i<m; i++) //init
        dp[i][0]=dpp[i][0]=data[i][0]; //init
    for(int j=1; j<n; j++)
    {
        for(int i=0; i<m; i++) //right
            dp[i][j]=dpp[i][j]=min(dp[i][j-1]+data[i][j],dp[i][j]);
        for(int i=1; i<m; i++) //down
            dp[i][j]=min(dp[i][j],dp[i-1][j]+data[i][j]);
        for(int i=m-2; i>=0; i--) //up
            dpp[i][j]=min(dpp[i][j],dpp[i+1][j]+data[i][j]);
        for(int i=0; i<m; i++) //comebine
            dp[i][j]=dpp[i][j]=min(dp[i][j],dpp[i][j]);
    }
    for(int i=0; i<m; i++)
        if(ans>dp[i][n-1])
            ans=dp[i][n-1];
    printf("Answer: %d",ans);
    return 0;
}


/** 131 673 234 103 18 201 96 342 965 150 630 803 746 422 111 537 699 497 121 965 805 732 524 37 331 **/

Problem 83 Path sum: four ways

路径和：四个方向

注意：这是第81题的一个极具挑战性的版本。

在如下的5乘5矩阵中，从左上角到右下角任意地向上、向下、向左或向右移动的最小路径和为2297，由标注红色的路径给出。

131 673 234 103 18
201 96 342 965 150
630 803 746 422 111
537 699 497 121 956
805 732 524 37 331
在这个31K的文本文件matrix.txt（右击并选择“目标另存为……”）中包含了一个80乘80的矩阵，求出从左上角到右下角任意地向上、向下、向左或向右移动的最小路径和。

直接Dijkstra

#include<iostream>
#include<stdio.h>
#include<queue>
using namespace std;
#define INF 1e9
int const limit=80;

int mat[limit][limit],cnt=0;
int dist[limit*limit+5];
bool done[limit*limit+5]= {0};
struct Edge
{
    int to,cost;
    bool operator < (const Edge & e) const
    {
        return this->cost>e.cost;
    }
    Edge(int t=0,int c=INF):to(t),cost(c) {}
} edges[limit*limit][4];
int getN()
{
    char tmp;
    int n=0;
    do
    {
        tmp=getchar();
        if(tmp>='0'&&tmp<='9')
            n=n*10+int(tmp-'0');
    }
    while(tmp>='0'&&tmp<='9');
    return n;
}

void addEdge(int x,int y,int i,int j)
{
    if(i>=limit||j>=limit||i<0||j<0) return ;
    edges[x*limit+y][cnt++]=Edge(i*limit+j,mat[i][j]);
}

void read()
{
    for(int i=0; i<limit; i++) /// read from txt
        for(int j=0; j<limit; j++)
            mat[i][j]=getN();
    ///build Graph
    for(int i=0; i<limit; i++)
        for(int j=0; j<limit; j++)
        {
            cnt=0;
            addEdge(i,j,i,j+1);
            addEdge(i,j,i,j-1);
            addEdge(i,j,i-1,j);
            addEdge(i,j,i+1,j);
        }
}

void dijkstra(int s=0)
{
    priority_queue<Edge> pque;
    for(int i=0; i<limit*limit; i++) dist[i]=INF;
    dist[s]=mat[0][0];
    pque.push(Edge(s,mat[0][0]));
    while(!pque.empty())
    {
        Edge x=pque.top();pque.pop();
        int u=x.to;
        if(done[u]) continue;
        done[u]=true;
        for(int i=0; i<4; i++)
        {
            Edge & e=edges[u][i];
            if(dist[e.to]>dist[u]+e.cost)
            {
                dist[e.to]=dist[u]+e.cost;
                pque.push(Edge(e.to,dist[e.to]));
            }
        }
    }
    cout<<dist[limit*limit-1]<<endl;
}
int main()
{
    freopen("p83in.txt","r",stdin);
    read();
    dijkstra();
    return 0;
}

Problem 84 Monopoly odds

大富翁几率

大富翁游戏的标准棋盘大致如下图所示：

| GO | A1 | CC1 | A2 | T1 | R1 | B1 | CH1 B2| B3 | JAIL |
| H2 | :————————————————- | C1 |
| T2 | :————————————————- | U1 |
| H1 | :————————————————- | C2 |
| CH3 | :————————————————- | C3 |
| R4 | :————————————————- | R2 |
| G3 | :————————————————- | D1 |
| CC3 | :————————————————- | CC2 |
| G2 | :————————————————- | D2 |
| G1 | :————————————————- | D3 |
| G2J | F3 | U2 | F2 | F1 | R3 | E3 | E2 | CH2 | E1 | FP |
玩家从标记有“GO”的方格出发，掷两个六面的骰子并将点数和相加，作为本轮他们前进的步数。如果没有其它规则，那么落在每一格上的概率应该是2.5%。但是，由于“G2J”（入狱）、“CC”（宝箱卡）和“CH”（机会卡）的存在，这个分布会有所改变。

除了落在“G2J”上，或者在“CC”或“CH”上抽到入狱卡之外，如果玩家连续三次都掷出两个相同的点数，则在第三次时将会直接入狱。

游戏开始时，“CC”和“CH”所需的卡片将被洗牌打乱。当一个玩家落在“CC”或“CH”上时，他们从宝箱卡和机会卡的牌堆最上方取一张卡并遵循指令行事，并将该卡再放回牌堆的最下方。宝箱卡和机会卡都各有16张，但我们只关心会影响到移动的卡片，其它的卡片我们都将无视它们的效果。

宝箱卡 (2/16 张卡):
回到起点“GO”
进入监狱“JAIL”
机会卡 (10/16 张卡):
回到起点“GO”
进入监狱“JAIL”
移动到“C1”
移动到“E3”
移动到“H2”
移动到“R1”
移动到下一个“R”（铁路公司）
移动到下一个“R”
移动到下一个“U”（公共服务公司）
后退三步
这道题主要考察掷出骰子后停在某个特定方格上的概率。显然，除了停在“G2J”上的可能性为0之外，停在“CH”格的可能性最小，因为有5/8的情况下玩家会移动到另一格。我们不区分是被送进监狱还是恰好落在监狱“JAIL”这一格，而且不考虑需要掷出两个相同的点数才能出狱的要求，而是假定进入监狱的第二轮就会自动出狱。

从起点“GO”出发，并将方格依次标记00到39，我们可以将这些两位数连接起来表示方格的序列。

统计学上来说，三个最有可能停下的方格分别是“JAIL”（6.24%）或方格10，E3（3.18%）或方格24以及“GO”（3.09%）或方格00。这三个方格可以用一个六位数字串表示：102400。

如果我们不用两个六面的骰子而是用两个四面的骰子，求出三个最有可能停下的方格构成的数字串。
模拟题，直接按题目意思进行模拟就行

#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#include <algorithm>
using namespace std;

int chances[41] = {0, 0, 10, 11, 24, 39, 5};
int utilities[41] = {0};
int rails[41] = {0};
int limit = 1000000;
int result[41] = {0};
void init()
{
    rails[7] = 12;
    rails[22] = 25;
    rails[36] = 5;
    utilities[7] = 12;
    utilities[22] = 28;
    utilities[36] = 12;
}

int rand_int(int a, int b)
{
    return (rand() % b) + a;
}

int main()
{
    int pos = 0, num = 0;
    int r1, r2, r3, r4;
    srand(time(NULL));
    init();
    while(limit --)
    {
        r1 = rand_int(1, 4);
        r2 = rand_int(1, 4);
        pos += r1 + r2;
        pos %= 40;
        num = (r1 == r2) ? num + 1 : 0;
        if(pos == 2 || pos == 17 || pos == 33)
        {
            r3 = rand_int(1, 16);
            if(r3 == 1)
                pos = 0;
            else if(r3 == 2)
                pos = 10;
        }
        if(rails[pos])
        {
            r4 = rand_int(1, 16);
            if(r4 < 7)
                pos = chances[r4];
            else if(r4 == 7 || r4 == 8)
                pos = rails[pos];
            else if(r4 == 9 )
                pos = utilities[pos];
            if(r4 == 10)
                pos = (pos + 37) % 40;
        }
        if(pos == 30 || num == 3)
            pos = 10;
        if(num == 3)
            num = 0;
        result[pos] += 1;
    }
    for(int i = 0; i < 41; i++)
        result[i] = result[i] * 100 + i;
    sort(result, result + 41);
    int ans = 0;
    for(int i = 0; i < 3; i++)
        ans = ans * 100 + (result[40 - i]) % 100;
    printf("ans: %d\n", ans);
    return 0;
}

Problem 85 Counting rectangles

数长方形

如果数得足够仔细，能看出在一个3乘2的长方形网格中包含有18个不同大小的长方形，如下图所示：

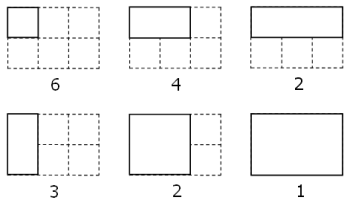
尽管没有一个长方形网格中包含有恰好两百万个长方形，但有许多长方形网格中包含的长方形数目接近两百万，求其中最接近这一数目的长方形网格的面积。
动态规划，可以求出递推公式

dp[j][i]=dp[i][j]=dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1]+i*j;
//dp[i][j]为边长为i,j的矩形包含的矩形的数目

#include<iostream>
#include<time.h>
using namespace std;

const int limit=500;
long long  rect[limit][limit]={0};
int ans,delt=200;
template<typename T>
T abs(T a)
{
    return a>0?a:-a;
}
int main()
{
    int start=clock();
    for(int i=1;i<limit;i++)
        for(int j=1;j<=i;j++)
        {
            rect[j][i]=rect[i][j]=rect[i-1][j]+rect[i][j-1]-rect[i-1][j-1]+i*j;
            if(abs(rect[i][j]-2000000)<= delt)
            {
                ans=i*j;
                delt=abs(rect[i][j]-2000000);
            }
        }
    cout<<ans<<endl;
    cout<<clock()-start<<"ms"<<endl;
    return 0;
}

Problem 86 Cuboid route

长方体路径

蜘蛛S位于一个6乘5乘3大小的长方体屋子的一角，而苍蝇F则恰好位于其对角。沿着屋子的表面，从S到F的最短“直线”距离是10，路径如下图所示：

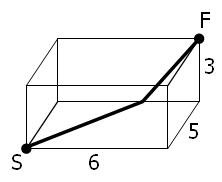
然而，对于任意长方体，“最短”路径实际上一共有三种可能；而且，最短路径的长度也并不一定为整数。

当M=100时，若不考虑旋转，所有长、宽、高均不超过M且为整数的长方体中，对角的最短距离是整数的恰好有2060个；这是使得该数目超过两千的最小M值；当M=99时，该数目为1975。

找出使得该数目超过一百万的最小M值。
暴力枚举

#include<iostream>
#include<math.h>
using namespace std;
#define eps 0.000000001
int cnt=0;
void inline check(int a,int b,int c)
{
    int x=a*a+(b+c)*(b+c),y=b*b+(a+c)*(a+c),z=c*c+(a+b)*(a+b);
    if(y<x) x=y;
    if(z<x) x=z;
    int tmp=sqrt(x)+eps;
    if(tmp*tmp==x) cnt++;
}
int main()
{
    for(int lim=1;lim<5000;lim++)
    {
        for(int j=1;j<=lim;j++)
            for(int k=j;k<=lim;k++)
                check(lim,j,k);
        if(cnt>1000000)
        {
            cout<<lim<<endl;
            cout<<cnt<<endl;
            break;
        }
    }
    return 0;
}

Problem 87 Prime power triples

素数幂三元组

最小的可以表示为一个素数的平方，加上一个素数的立方，再加上一个素数的四次方的数是28。实际上，在小于50的数中，一共有4个数满足这一性质：

28=22+23+24
33=32+23+24
49=52+23+24
47=22+33+24

有多少个小于五千万的数，可以表示为一个素数的平方，加上一个素数的立方，再加上一个素数的四次方？
暴力求解即可

#include<iostream>
#include<set>

using namespace std;
const int limit=50000000;
int prime[10000],nprime=0;
bool have[limit+1]={0};

int main()
{
    for(int i=2; i<10000; i++)
    {
        bool f=true;
        for(int j=2; j*j<=i; j++)
            if(i%j==0)
            {
                f=false;
                break;
            }
        if(f)
            prime[nprime++]=i;
    }
    for(int i=0; prime[i]<=7071; i++)
        for(int j=0; prime[j]<=386; j++)
            for(int k=0; prime[k]<=84; k++)
            {
                int tmp=prime[i]*prime[i]+prime[j]*prime[j]*prime[j]+prime[k]*prime[k]*prime[k]*prime[k];
                if(tmp<=50000000)
                   have[tmp]=true;
            }
    int ans=0;
    for(int i=1;i<=limit;i++)
        if(have[i]) ans++;
    cout<<ans<<endl;
    return 0;
}

Problem 88 Product-sum numbers

积和数

若自然数N能够同时表示成一组至少两个自然数{a1, a2, … , ak}的积和和，也即N = a1 + a2 + … + ak = a1 × a2 × … × ak，则N被称为积和数。

例如，6是积和数，因为6 = 1 + 2 + 3 = 1 × 2 × 3。

给定集合的规模k，我们称满足上述性质的最小N值为最小积和数。当 k=2、3、4、5、6 时，最小积和数如下所示：

k=2:4=2×2=2+2
k=3:6=1×2×3=1+2+3
k=4:8=1×1×2×4=1+1+2+4
k=5:8=1×1×2×2×2=1+1+2+2+2
k=6:12=1×1×1×1×2×6=1+1+1+1+2+6

因此，对于2≤k≤6，所有的最小积和数的和为 4+6+8+12=30 ；注意8只被计算了一次。

已知对于2≤k≤12，所有最小积和数构成的集合是{4, 6, 8, 12, 15, 16}，这些数的和是61。

对于2≤k≤12000，所有最小积和数的和是多少？
也是暴力的方法，不过反向生成，而不是枚举判断

#include<stdio.h>
#define MAXN 12000
int psnk[(MAXN + 5)] = {0};
int exist[MAXN << 2] = {0};

void getPSN(int n, int sum, int product_cnt)
{
    int k = n - sum + product_cnt, i;
    if(k > MAXN) return ;
    if(!psnk[k]  || psnk[k] > n)
        psnk[k] = n;
    for(i = 2; i * n <= MAXN * 2; i++)
        getPSN(n * i, sum + i, product_cnt + 1);
}

int main()
{
    int ans = 0, i;
    getPSN(1, 1, 1);
    for(i = 2; i <= MAXN; i++)
        if(!exist[psnk[i]])
        {
            exist[psnk[i]] = 1;
            ans += psnk[i];
        }
    printf("%d\n", ans);
    return 0;
}

Problem 89 Roman numerals

罗马数字

要正确地用罗马数字表达一个数，必须遵循一些基本规则。尽管符合规则的写法有时会多于一种，但对每个数来说总是存在一种“最好的”写法。

例如，数16就至少有六种写法：

IIIIIIIIIIIIIIII
VIIIIIIIIIII
VVIIIIII
XIIIIII
VVVI
XVI

然而，根据规则，只有XIIIIII和XVI是合理的写法，而后一种因为使用了最少的数字而被认为是最有效的写法。

在这个11K的文本文件roman.txt （右击并选择“目标另存为……”）中包含了一千个合理的罗马数字写法，但并不都是最有效的写法；有关罗马数字的明确规则，可以参考关于罗马数字。

求出将这些数都写成最有效的写法所节省的字符数。

注意：你可以假定文件中的所有罗马数字写法都不包含连续超过四个相同字符。
这个有简便方法，就直接找出冗余的写法，实际上只有少数几种冗余的写法如VIIII之类的，全部找出来，直接用正则表达式类的方法很好得到答案
如

X=((b'IIII',2),(b'XXXX',2),(b'CCCC',2),(b'VIIII',1),(b'LXXXX',1),(b'DCCCC',1))
with open('p089_roman.txt', 'rb') as f: s = f.read()
print(sum([s.count(num) * x for num, x in X]))

或者

print sum([len(x) - len(re.sub('DCCCC|LXXXX|VIIII|CCCC|XXXX|IIII','aa',x)) for x in  open("roman.txt")])

当然我用的是C写的普通方法,先将罗马数字转换成整数，再转换成罗马数字，虽然麻烦了点但是速度很快

#include <stdio.h>
#include <string.h>


int table[256] = {0};
int num[] = {1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1};
char chrs[][5] = {"M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"};
int roman2int( char * str)
{
    int ans = 0, last = 0, now = 0;
    while(*str)
    {
        now = table[*(str++)];
        ans += now;
        if(last < now)
            ans -= (last << 1);
        last = now;
    }
    return ans;
}

void int2roman(int n, char str[])
{
    int idx = 0, i = 0;
    while(n)
    {
        while(n < num[i]) i++;
        n -= num[i];
        str[idx++] = chrs[i][0];
        if(i & 1)
            str[idx++] = chrs[i][1];
    }
    str[idx] = 0;
}
void init()
{
    table['i'] = table['I'] = 1;
    table['v'] = table['V'] = 5;
    table['x'] = table['X'] = 10;
    table['l'] = table['L'] = 50;
    table['c'] = table['C'] = 100;
    table['d'] = table['D'] = 500;
    table['m'] = table['M'] = 1000;
}
char rmn[100] = {0};
char ans_char[100];
int main()
{
    init();
    freopen("p089_roman.txt", "r", stdin);
    //freopen("p089_roman_min.txt","w",stdout);
    int all_len = 0;
    int origin_len = 0;
    while(~scanf("%s", rmn))
    {
        //printf("%s ",rmn);
        int n = roman2int(rmn);
        origin_len += strlen(rmn);
        int2roman(n, ans_char);
      // printf("%s %s\n",rmn,ans_char);
        all_len += strlen(ans_char);
    }
    printf("origin %d minimal %d ans: %d\n",origin_len,all_len,origin_len - all_len);
    return 0;
}

Problem 90 Cube digit pairs

立方体数字对

在一个立方体的六个面上分别标上不同的数字（从0到9），对另一个立方体也如法炮制。将这两个立方体按不同的方向并排摆放，我们可以得到各种各样的两位数。

例如，平方数64可以通过这样摆放获得：

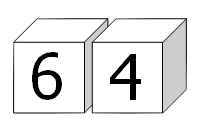
事实上，通过仔细地选择两个立方体上的数字，我们可以摆放出所有小于100的平方数：01、04、09、16、25、36、49、64和81。

例如，其中一种方式就是在一个立方体上标上{0, 5, 6, 7, 8, 9}，在另一个立方体上标上{1, 2, 3, 4, 8, 9}。

在这个问题中，我们允许将标有6或9的面颠倒过来互相表示，只有这样，如{0, 5, 6, 7, 8, 9}和{1, 2, 3, 4, 6, 7}这样本来无法表示09的标法，才能够摆放出全部九个平方数。

在考虑什么是不同的标法时，我们关注的是立方体上有哪些数字，而不关心它们的顺序。

{1, 2, 3, 4, 5, 6}等价于{3, 6, 4, 1, 2, 5}
{1, 2, 3, 4, 5, 6}不同于{1, 2, 3, 4, 5, 9}

但因为我们允许在摆放两位数时将6和9颠倒过来互相表示，这个例子中的两个不同的集合都可以代表拓展集{1, 2, 3, 4, 5, 6, 9}。

对这两个立方体有多少中不同的标法可以摆放出所有的平方数？

实际是暴力模拟题，枚举时使用二进位来表示每个数字是否出现在骰子上，复杂度并不高,6,9可以互换注意下就行

#include <stdio.h>

#define AB(x,y) (a[x]&b[y])
#define CC(x,y) (!(AB(x,y) || AB(y,x)))

#define A6 (a[6]|a[9])
#define B6 (b[6]|b[9])
#define C6(x) ( !((A6 & b[x])|| (B6 & a[x])))

int map[1<<22]={0};

int maybe(int n)
{
    int cnt=0;
    while(n)
    {
        cnt += n&1;
        n >>= 1;
    }
    return cnt == 6;
}
int check(int m,int n)
{
    int a[10]={0},b[10]={0},idx=0;
    while(m || n)
    {
        a[idx] = m & 1;
        b[idx++] = n & 1;
        m >>= 1;
        n >>= 1;
    }
    if(CC(0,1)) return 0;
    if(CC(0,4)) return 0;
    if(C6(0)) return 0;
    if(C6(1)) return 0;
    if(CC(2,5)) return 0;
    if(C6(3)) return 0;
    if(C6(4)) return 0;
    if(CC(1,8)) return 0;
    return 1;
}

int may[1024],may_cnt=0;
int main()
{
    int i,j,m,n,cnt = 0;
    for(i=1;i < 1024; i++)
        if(maybe(i))
            may[may_cnt++] = i;
    printf("%d\n",may_cnt);
    for(i=0;i < may_cnt; i++)
        for(j=0; j < may_cnt; j++)
            if(check(may[i],may[j]))
            {
                m = may[i]*1024 + may[j];///保存方案，来去重
                n = may[j]*1024 + may[i];
                if(map[m] || map[n]) continue;
                map[m]=map[n]=1;
                cnt ++;
            }
    printf("%d \n",cnt);
    return 0;
}