UVA 10163 Storage Keepers(两次DP)
UVA 10163 Storage Keepers(两次DP)
http://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=1104
题意:
有n个仓库(最多100个),m个管理员(最多30个),每个管理员有一个能力值P(接下来的一行有m个数,表示每个管理员的能力值).每个仓库只能由一个管理员看管,但是每个管理员可以看管k个仓库(但是这个仓库分配到的安全值只有p/k,k=0,1,..n. 其中p/k取整数部分), 每个月公司都要给看管员工资,雇用的管理员的工资即为他们的能力值p和,问,使每个仓库的安全值最高的前提下,使的工资总和最小。
输出最大安全值,并且输出最少的花费。
分析:
开始做这题的时候, 我没注意”每个仓库只能由一个管理员看管”.这个条件. 不过就算没有这个条件, 也可以证明最优情况下, 一定存在每个仓库只有一个管理员看管的解.证明如下:
假设存在安全值最高且工资总和最小的解, 且当前解存在某个仓库有2个人看管. 那么这个仓库的安全值肯定取决于给予该仓库安全值大的那个人, 所以另外一个人我们可以直接让他不要看管这个仓库了, 那么这个人要么还有其他仓库看管(那么其他仓库的安全值可能变得更高,可能得到一个更高的安全总值), 要么我们可以解雇他.(得到一个更少的工资数) 所以在每个仓库最多只有1个人看管的情况下, 我们得到的解反而可能更优. 所以我们只需要考虑每个仓库最多只有1个人看管的情况即可.
第一次DP过程,求最大安全总值.
令dp[i][j]==x表示前i个人看管j个仓库时, 能获得的最大安全总值为x.
状态转移: dp[i][j]= max( dp[i-1][j] , min( dp[i-1][k], p[i]/(j-k) ) ) 其中0<=k<j.
前者表示第i个人不看管任何仓库, 后者表示第i个人至少要看管j-k个仓库(j-k的范围为[1,j]).
最终所求为: 最大安全总值L=dp[m][n]的值.
第二次DP过程, 求在最大安全总值==L的情况下, 总花费最小.
令dp[i][j]==x表示前i个人看管j个仓库且最大安全总值==L时, 最小花费为x.
状态转移: dp[i][j]= min(dp[i-1][j], dp[i-1][k]+p[i]). 其中0<=k<=j-1且要求p[i]/k>=L.
前者表示第i个人不看管任何仓库, 后者表示第i个人至少要看管j-k个仓库.(j-k属于范围[1,j])
最终所求为: 最小开销为Y=dp[m][n]的值.
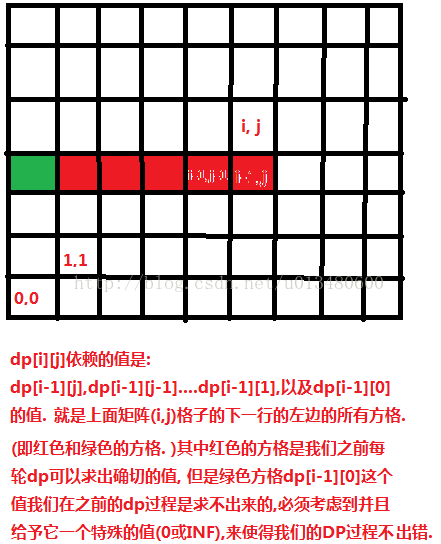
上面说完了dp过程, 但是最容易错的不在dp, 而在dp数组的初始化问题上. 下面源代码给了两份, 其中第一份是统一初始化dp数组, 但是对于边界特殊情况特殊处理了. 第二份是分类初始化dp数组, 但是就不用处理标记的特殊情况了. 具体原理其实就是一个二维矩阵:
AC代码1:统一初始化dp数组并作特殊处理
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define INF 1e8
const int maxn=100+5;
int n,m;
int p[maxn];
int dp[maxn][maxn];
int L,Y;
bool solve()
{
//dp[i][j]表前i个人看管j个仓库的最大安全总值
memset(dp,0,sizeof(dp));
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
{
dp[i][j]=dp[i-1][j];
if(i==1) //i==1,只有1个人时
dp[i][j]=max(dp[i][j],p[i]/j);
else //i>=2
{
for(int k=0;k<j;k++)//前i-1人管理k个仓库,第i人管理j-k个仓库
{
if(k==0) dp[i][j]=max(dp[i][j], p[i]/j);
else
dp[i][j]=max(dp[i][j], min(dp[i-1][k] , p[i]/(j-k)) );
}
}
}
if(!dp[m][n]) return false;
L=dp[m][n];
//dp[i][j]表前i个人看管j个仓库的最小花费
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
dp[i][j]=INF;
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
{
if(i==1)//i==1,只有1个人
{
if(p[i]/j>=L) dp[i][j]=p[i];
}
else //i>=2
{
dp[i][j]=min(dp[i][j], dp[i-1][j]);
for(int k=0;k<j;k++)//前i-1个人管理k个仓库
if(k==0)
{
if(p[i]/j>=L)
dp[i][j]=min(dp[i][j], p[i]);
}
else
{
if(p[i]/(j-k)>=L)
dp[i][j]=min(dp[i][j], dp[i-1][k]+p[i]);
}
}
}
Y=dp[m][n];
return true;
}
int main()
{
while(scanf("%d%d",&n,&m)==2 && n)
{
for(int i=1;i<=m;i++)
scanf("%d",&p[i]);
if(solve())
printf("%d %d\n",L,Y);
else printf("0 0\n");
}
return 0;
}
AC代码2:分类初始化, 不用处理边界.
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define INF 1e8
const int maxn=100+5;
int n,m;
int p[maxn];
int dp[maxn][maxn];
int L,Y;
bool solve()
{
//dp[i][j]表前i个人看管j个仓库的最大安全总值
for(int i=0;i<=m;i++)
dp[i][0]=INF;
for(int i=1;i<=n;i++)
dp[0][i]=0;
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
{
dp[i][j]=dp[i-1][j];
for(int k=0;k<j;k++)//前i-1人管理k个仓库,第i人管理j-k个仓库
dp[i][j]=max(dp[i][j], min(dp[i-1][k] , p[i]/(j-k)) );
}
if(!dp[m][n]) return false;
L=dp[m][n];
//dp[i][j]表前i个人看管j个仓库的最小花费
for(int i=0;i<=m;i++)
dp[i][0]=0;
for(int i=1;i<=n;i++)
dp[0][i]=INF;
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
{
dp[i][j]=dp[i-1][j];
for(int k=0;k<j;k++)//前i-1个人管理k个仓库
if(p[i]/(j-k)>=L)
dp[i][j]=min(dp[i][j], dp[i-1][k]+p[i]);
}
Y=dp[m][n];
return true;
}
int main()
{
while(scanf("%d%d",&n,&m)==2 && n)
{
for(int i=1;i<=m;i++)
scanf("%d",&p[i]);
if(solve())
printf("%d %d\n",L,Y);
else printf("0 0\n");
}
return 0;
}