POJ 1151 - Atlantis 线段树+扫描线..

   离散化: 将所有的x轴坐标存在一个数组里..排序.当进入一条线段时..通过二分的方式确定其左右点对应的离散值...

   扫描线..可以看成一根平行于x轴的直线..至y=0开始往上扫..直到扫出最后一条平行于x轴的边..但是真正在做的时候..不需要完全模拟这个过程..扫描线的做法是从最下面的边开始扫到最上面的边.

   线段树: 本题用于动态维护扫描线在往上走时..x哪些区域是有合法面积的..

   几个图说明扫描线扫描..线段树维护的过程..:

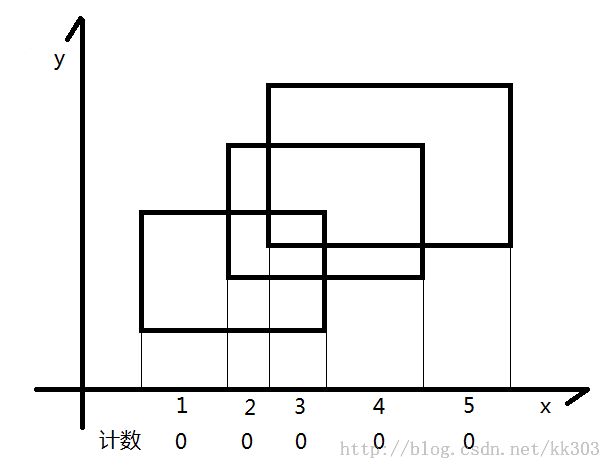
初始状态

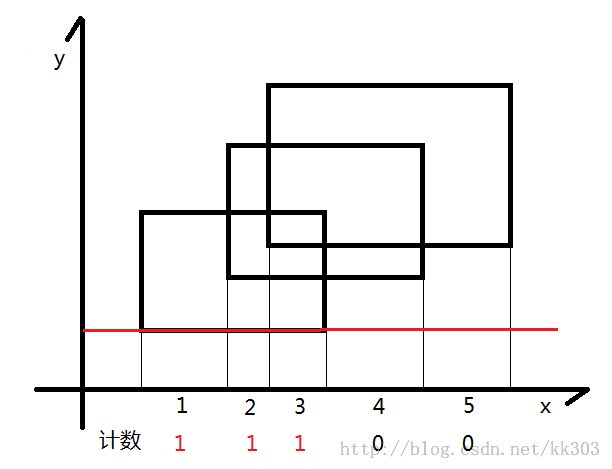
扫到最下边的线,点更新1~3为1

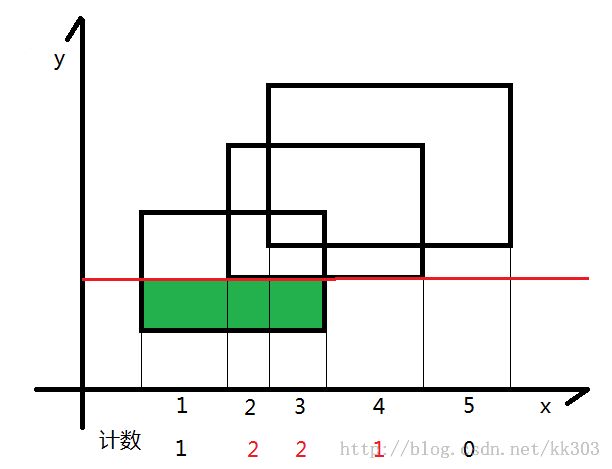
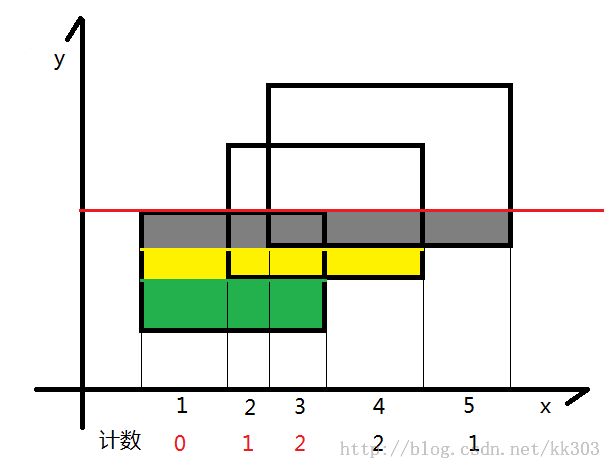
扫到第二根线,此时将计数器不为0的长度*上线两根线的长度,得到绿色的面积,加到答案中去.随后更新计数

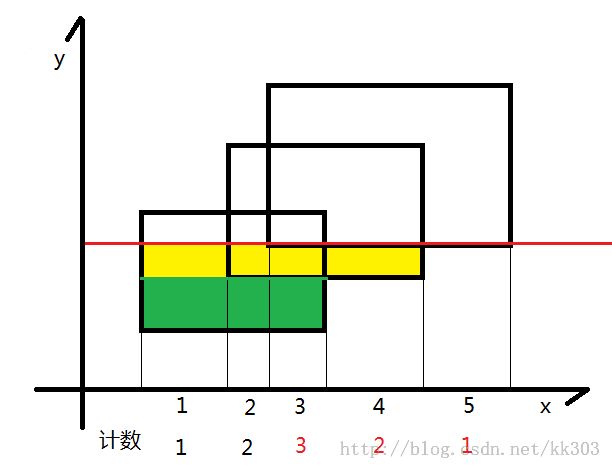
同上,将黄色的面积加到答案中去

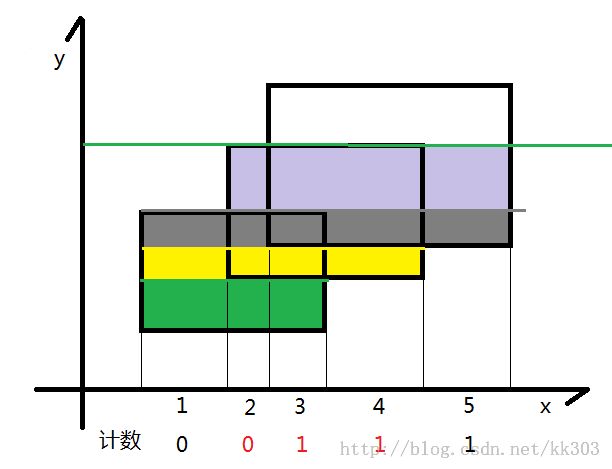
同上,将灰色的面积加到答案中去

同上,将紫色的面积加到答案中去

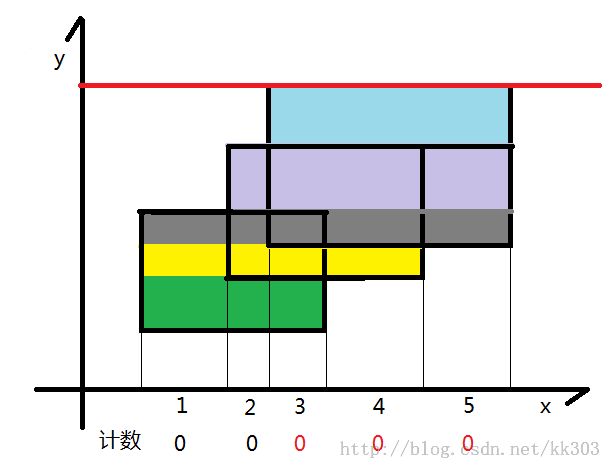
同上,将蓝色的面积加到答案中去

Program:

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<set>
#include <ctime>
#include<queue>
#include<algorithm>
#include<cmath>
#define oo 1000000007
#define ll long long
#define pi acos(-1.0)
#define MAXN 405
using namespace std;
struct node
{
      double l,r,y;
      int tp;
      bool operator <(node a) const
      {
            return y<a.y;
      }
}line[MAXN<<2];
int n,Times[MAXN<<2];
double X[MAXN<<2],sum[MAXN];
int b_search(double x)
{
      int l,r,mid;
      l=0,r=n+1;
      while (r-l>1)
      {
            mid=(l+r)>>1;
            if (X[mid]<=x) l=mid;
               else r=mid;
      }
      return l;
}
void update(int x,int c,int l,int r,int now)
{
      if (l==r)
      {
            Times[x]+=c;
            if (Times[x]) sum[now]=X[x+1]-X[x];
            if (!Times[x]) sum[now]=0;
            return;
      }
      int mid=(l+r)/2;
      if (x<=mid) update(x,c,l,mid,now<<1);
      if (mid<x)  update(x,c,mid+1,r,(now<<1)|1);
      sum[now]=sum[now<<1]+sum[(now<<1)|1];
      return;
}
int main()
{ 
      int i,j,num,T=0;
      double ans=0; 
      while (~scanf("%d",&n) && n)
      {
            num=0;
            for (i=1;i<=n;i++)
            {
                   double x1,y1,x2,y2;
                   scanf("%lf%lf%lf%lf",&x1,&y1,&x2,&y2);
                   line[i*2-1].y=y1,line[i*2-1].l=x1,line[i*2-1].r=x2,line[i*2-1].tp=1;
                   line[i*2].y=y2,line[i*2].l=x1,line[i*2].r=x2,line[i*2].tp=-1;
                   X[++num]=x1,X[++num]=x2;
            }
            n=n*2;
            sort(X+1,X+1+num);
            sort(line+1,line+1+n);
            memset(sum,0,sizeof(sum));
            memset(Times,0,sizeof(Times));
            ans=0;
            for (i=1;i<=n;i++)
            {
                   ans+=sum[1]*(line[i].y-line[i-1].y); 
                   int l,r;
                   l=b_search(line[i].l);
                   r=b_search(line[i].r)-1;
                   for (j=l;j<=r;j++) update(j,line[i].tp,1,n-1,1);
            }
            printf("Test case #%d\nTotal explored area: %.2f\n\n",++T,ans);
      }
      return 0;
}