DES加密实现(翻译自书籍《Wiley.Implementing.SSL.TLS.Using.Cryptography.and.PKI》)
理解BlockCipher加密算法
- 凯撒大帝被认为是最古老的对称加密算法。所谓的凯撒加密法(你也许可以从报纸上找到一个作为消遣来玩),它随机的给每一个字母分配一个数字。在这个简单的算法当中,字母到数字的映射就是key。现代加密算法比凯撒算法肯定复杂的多,以便抵御来自计算机的攻击。尽管基本原理是一样,替换一个字母或其它什么东西为另外一个字母或其它什么东西,后续都对替换后的东西进行处理,在几个世纪以来,更多的混淆和扩散(confusion and diffusion)要素被加入,从而创建了现代加密算法。一个很重要的技术就是同时操作一组字符,而不是一个。现在用的最多的对称加密算法类别就是块加密算法,它对固定数目的字节进行操作,而不是一个字符。
- 在这一部分我们来考察3种最流行的块加密算法,也是我们在工作中最可能碰到的现代加密算法。这些算法也许会在未来几十年还有意义,要修改加密标准,那个过程是非常非常慢的;需要密码专家进行大量的研究和分析。
实现DES加密算法
- DES是Data Encryption Standard(数据加密标准)的简称,它是1974年,在NSA的要求下,由IBM实现和提出的;它也是第一个可以公开获取的针对计算机的加密算法。尽管在后文你看可以看到,DES不再认为是足够安全的,但是它还在被广泛地使用着。并且它也是学习对称加密算法的好入口。DES中的绝大多数概念都会在其它加密算法中出现。
- DES将输入分成8字节的块,然后使用一个8字节的key来混淆它们。这个混淆的过程有一系列的固定置换(将第34位和28位互换,28位和17位互换等等)、轮换以及XORs。尽管DES的核心(也就是DES为什么是安全的)是因为S boxes的操作,经过它输入的每6个bit,都会固定地4bit的输出;但是这个过程是不可逆的(除非有key)。
- 和任何现代对称加密算法一样,DES也非常依赖于XOR操作。【异或操作介绍略】
- 异或一个非常有趣的属性就是它是可逆的,比如:

- 在实现DES的时候,我们一般操作的是字节数组,以便充分利用硬件对整数操作的优势。传统上,DES是使用大端来描述的,但是x86等架构都是小端的;为了充分利用硬件性能,我们需要对规范中的一些部分进行反转,不过在这里,我们不需要这么做
- 作为一个替代方案,我们操作byte数组。因为我们需要操作位,比如:得到64bit中的第39个bit的值;因此我们需要一些宏的支持,从而可以方便的对字节数组进行bit查找和操作。bit操作的宏如下所示:
#define GET_BIT( array, bit ) \
( array[( int ) ( bit /8 ) ] & ( 0x80 >> (bit % 8 ) ) )
#define SET_BIT( array, bit ) \
( array[( int ) ( bit /8 ) ] |= ( 0x80 >> (bit % 8 ) ) )
#define CLEAR_BIT( array, bit ) \
( array[( int ) ( bit /8 ) ] &= ~( 0x80>> ( bit % 8 ) ) )
- 因为这个例子是对字节数组求异或的,所以需要一个方法来支持异或操作。
static void xor( unsignedchar *target, constunsigned char *src, int len )
{
while ( len-- )
{
*target++^= *src++;
}
}
- 最后我们还需要一个置换(permute)函数,这个函数根据 permute_table数组对输入进行bit置换,比如:输入的第57bit放到输出的第14bit。正如你下面会看到的,这个函数是DES算法调用最频繁的地方;它被调用了10多次(使用不同的置换表permute_table)
/**
* Implement the initialand final permutation functions. permute_table
* and target must haveexactly len and len * 8 number of entries,
* respectively, but srccan be shorter (expansion function depends on this).
* NOTE: this assumesthat the permutation tables are defined as one-based
* rather than 0-basedarrays, since they’re given that way in the
* specification.
*/
static void permute( unsignedchar target[],
const unsigned char src[],
const int permute_table[],
int len )
{
int i;
for ( i = 0; i <len * 8; i++ )
{
if ( GET_BIT( src,( permute_table[ i ]- 1 ) ) )
{
SET_BIT(target, i );
}
else
{
CLEAR_BIT( target, i );
}
}
}
DES初始置换
- DES规范中要求对输入进行一个初始置换。这个置换的目的是什么还不是很清楚,因为它没有任何加密的效果(置换后的安全效果和置换前是一样的)。加入这个置换的目的,也许是为了对某些硬件类型进行优化。尽管如此,如果你不进行这个操作,你的DES加密结果将会是错误的,也不能够和其它实现进行交互。
- 在规范中,对这个置换的描述使用术语:input bits和output bits。它的操作如下:将input最后一个字节的第2个bit拷贝到output第一个字节的第一个bit;然后将input倒数第二个字节的第2个bit拷贝到output第一个字节的第2个bit等等。因此,output的第一个字节是由input左右字节中的第2个bit组成的(反向的)。output的第2个字节是input每个字节的第4个bit组成的(也是反向的)。output的第3个字节是input每个字节的第6个bit组成的,output的第4个字节由input每个字节的第8个bit组成,output的第5个字节由input每个字节的第1个字节组成,等等。
- 故给定8个字节作为输入,操作的结果如下:
- 实现这个置换可以使用前面的置换(permute)函数,其中permute_table如下:(注意:DES认为字节序是大端的)
比如:第一个字节是由原字节数组中,每个字节的第2个bit组成。
原字节数组位数的大小,从左到有为:1到64,上图字节数组中标识为1的为58,2为50等等
static const int ip_table[] = {
58, 50, 42, 34, 26, 18, 10, 2,
60, 52, 44, 36, 28, 20, 12, 4,
62, 54, 46, 38, 30, 22, 14, 6,
64, 56, 48, 40, 32, 24, 16, 8,
57, 49, 41, 33, 25, 17, 9, 1,
59, 51, 43, 35, 27, 19, 11, 3,
61, 53, 45, 37, 29, 21, 13, 5,
63, 55, 47, 39, 31, 23, 15, 7 };
- 在输入被置换之后, 它又被用key进行了16轮的操作组合,每一轮做的操作如下:
- 扩展输入的第32到第64位到48bits(下面会进行描述)
- 将扩展后的右边部分和key做XOR
- 使用上面的输出,查询8个s-box表,并使用这些内容来覆盖输入
- 根据特定的p表来对输出进行置换
- 将输出和输入的左边部分(1~32)做XOR,然后对左右部分交换;在下一轮,相同的操作被执行,但是左右部分被调换了
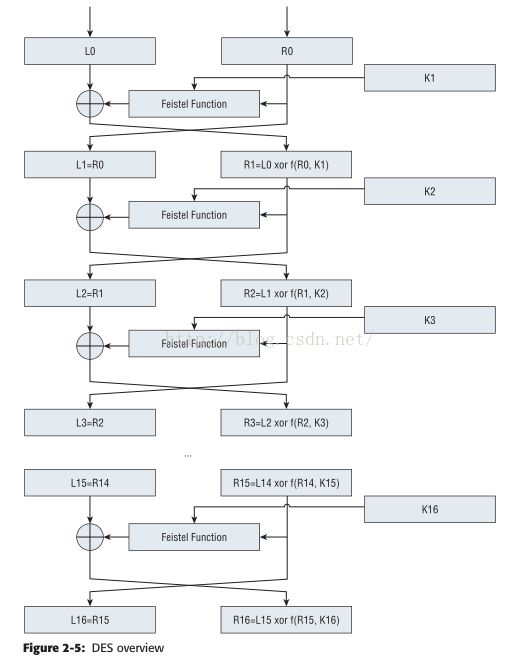
- 最终,前后部分做最后一次交换,然后对输出做初始置换的反操作,也就抵消了初始置换。
/**
* This just invertsip_table.
*/
static const int fp_table[] = { 40, 8, 48, 16, 56, 24, 64, 32,
39, 7, 47, 15, 55, 23, 63, 31,
38, 6, 46, 14, 54, 22, 62, 30,
37, 5, 45, 13, 53, 21, 61, 29,
36, 4, 44, 12, 52, 20, 60, 28,
35, 3, 43, 11, 51, 19, 59, 27,
34, 2, 42, 10, 50, 18, 58, 26,
33, 1, 41, 9, 49, 17, 57, 25 }
上面是最后使用的置换表。
DES Key Schedule
- 在算法描述的第2步中,“将扩展后的右边部分和key做XOR”。如果我们看了图,就会发现,图中的key,分别标记为K1,K2、K3…K15、K16. 也就是说有16个不同的48bit的key,他们都是通过原始的64bit的key产生的。
- key经过的初始之后和输入的初始置换很类似,但是还是有点不同,输出的第一个字节是由输入的每个字节的第一个bit组成的,输出的第二个字节是由输入的每个字节的第2个bit组成的,等等。
- 但是key本身使用2个28-bit部分来组成;第2个部分的第一个字节由输入的每个字节的第7个bit组成,第2个字节由输入的每个字节的第6个bit组成等等。由于key的一半是28bit(3个字节加上4个bit),最后的4个bit也是这个规则生成的,但是只对前4个bit这么做。最终,虽然输入的key为8个字节,输出的key只有2个28bit部分,也就是56bit。其余8个bit(每个字节的第8bit)没有被DES使用。
上面的操作可以使用下面的置换表来完成:
static const int pc1_table[] = { 57, 49, 41, 33, 25, 17, 9, 1,
58, 50, 42, 34, 26, 18, 10, 2,
59, 51, 43, 35, 27, 19, 11, 3,
60, 52, 44, 36,
63, 55, 47, 39, 31, 23, 15, 7,
62, 54, 46, 38, 30, 22, 14, 6,
61, 53, 45, 37, 29, 21, 13, 5,
28, 20, 12, 4 };
- 在上述算法中的每一轮中,56-bit的key的每个28bit部分,会被向左轮换1或2次,1次是在第1,2,9,16轮中,其它轮次2次。这些轮换后的部分会使用下面的置换表进行置换:
static const int pc2_table[] = { 14, 17, 11, 24, 1, 5,
3, 28, 15, 6, 21, 10,
23, 19, 12, 4, 26, 8,
16, 7, 27, 20, 13, 2,
41, 52, 31, 37, 47, 55,
30, 40, 51, 45, 33, 48,
44, 49, 39, 56, 34, 53,
46, 42, 50, 36, 29, 32 };
- 这个置换可以从轮换后的56bit key中产生48bit的subkey。因为做了轮换,所以算法的每一轮都有一个唯一key,K1、K2、K3.。。。K16。这些subkeys被称为key schedule。
- 注意到key schedule和加密操作是独立的,能够预先计算好,在加密或解密之前存储起来。绝大多数的DES实现为了提升性能都是这么做的。
- 56bit key的左轮换的代码如下:
/**
* Perform the leftrotation operation on the key. This is made fairly
* complex by the factthat the key is split into two 28-bit halves, each
* of which has to berotated independently (so the second rotation operation
* starts in the middleof byte 3).
*/
static void rol( unsigned char *target )
{
intcarry_left, carry_right;
carry_left= ( target[ 0 ] & 0x80 ) >> 3;
target[ 0 ] =( target[ 0 ]<< 1 ) | (( target[ 1 ]& 0x80 ) >> 7 );
target[ 1 ] =( target[ 1 ]<< 1 ) | (( target[ 2 ]& 0x80 ) >> 7 );
target[ 2 ] =( target[ 2 ]<< 1 ) | (( target[ 3 ]& 0x80 ) >> 7 );
// special handling forbyte 3
carry_right= ( target[ 3 ] & 0x08 ) >> 3;
target[ 3 ] =( ( ( target[ 3 ]<< 1 ) | (( target[ 4 ]& 0x80 ) >> 7 ) ) &~0x10 ) | carry_left;
target[ 4 ] =( target[ 4 ]<< 1 ) | (( target[ 5 ]& 0x80 ) >> 7 );
target[ 5 ] =( target[ 5 ]<< 1 ) | (( target[ 6 ]& 0x80 ) >> 7 );
target[ 6 ] =( target[ 6 ]<< 1 ) | carry_right;
}
通过上面我们可以看到,key的每个字节(在一个7字节数组中)都被左移一位。下一个字节的MSB是LSB;复杂的地方在于key是一个7字节数组,但是这7字节数组分割在第3个字节的中间。
DES Expansion Function
- 注意到前面提到的subkey是48bit长的,但是输入的一半是(L0或R0)32bit的。当前,我们不能够很好的将32bit的输入和48bit的key进行XORs操作。因此,为了和48bit的key进行XOR操作,输入需要进行扩充(对一些bit进行复制)。扩充的输出见下图:
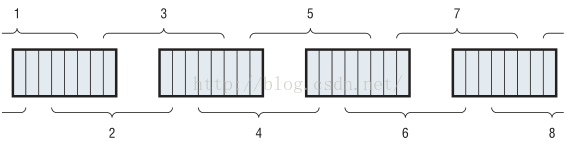
输出被分成8个6bit的块(也就是6个字节),每个块的前两个和后两个bit在前一个块和后一个块是重叠的。同时第一个块和最后一个块是循环重叠,使用输入的最后一个bit作为第一个块的第一个bit,使用输入的第一个bit作为最后一个块的最后一个bit。当然,这些操作也可以使用置换表来进行,表的结构如下:
static const intexpansion_table[] = {
32, 1, 2, 3, 4, 5,
4, 5, 6, 7, 8, 9,
8, 9, 10, 11, 12, 13,
12, 13, 14, 15, 16, 17,
16, 17, 18, 19, 20, 21,
20, 21, 22, 23, 24, 25,
24, 25, 26, 27, 28, 29,
28, 29, 30, 31, 32, 1 };
- 在每一轮中,输入的字节在和subkey进行XOR之后,结果被送入s-box进行查询。s-boxes是DES安全的关键所在。它的一个特性非常重要:输出和输入不是线性关系,否则的话,一个简单的统计分析就可以把key解密出来。比如:攻击者知道字母E是英语中出现频率最多的字符(如果他也知道文件是按照ASCII进行编码的),它可以对输出的字节进行频率统计,找到出现最频繁的,然后假定它就是E,然后进行反推(事实上,在ASCII编码的英文文档,出现最多的是空格,字符编码为32)。如果错了,他就对出现频率第二多的字符进行重试。这类密码分析,使用计算机的话只需要几秒钟就可以完成。因此,s-boxes不是置换表、轮换或XORs,而是由多个完全随机的表组成的。
- 输入的每6bit对应表中的4bit输出(expanded之后的右半部分和sub key进行XOR)。也就是说,每个6bit的输入作为索引去s-boxes去找对应的值。在DES规范中,s-boxes的描述很模糊。我们在这里使用更简洁,便于查询的方式来展示他们。注意:每6个bit都有它们自己的唯一sbox。
static const int sbox[8][64] = {
{ 14, 0, 4, 15, 13, 7, 1, 4, 2, 14, 15, 2, 11, 13, 8, 1,
3, 10, 10, 6, 6, 12, 12, 11, 5, 9, 9, 5, 0, 3, 7, 8,
4, 15, 1, 12, 14, 8, 8, 2, 13, 4, 6, 9, 2, 1, 11, 7,
15, 5, 12, 11, 9, 3, 7, 14, 3, 10, 10, 0, 5, 6, 0, 13 },
{ 15, 3, 1, 13, 8, 4, 14, 7, 6, 15, 11, 2, 3, 8, 4, 14,
9, 12, 7, 0, 2, 1, 13, 10, 12, 6, 0, 9, 5, 11, 10, 5,
0, 13, 14, 8, 7, 10, 11, 1, 10, 3, 4, 15, 13, 4, 1, 2,
5, 11, 8, 6, 12, 7, 6, 12, 9, 0, 3, 5, 2, 14, 15, 9 },
{ 10, 13, 0, 7, 9, 0, 14, 9, 6, 3, 3, 4, 15, 6, 5, 10,
1, 2, 13, 8, 12, 5, 7, 14, 11, 12, 4, 11, 2, 15, 8, 1,
13, 1, 6, 10, 4, 13, 9, 0, 8, 6, 15, 9, 3, 8, 0, 7,
11, 4, 1, 15, 2, 14, 12, 3, 5, 11, 10, 5, 14, 2, 7, 12 },
{ 7, 13, 13, 8, 14, 11, 3, 5, 0, 6, 6, 15, 9, 0, 10, 3,
1, 4, 2, 7, 8, 2, 5, 12, 11, 1, 12, 10, 4, 14, 15, 9,
10, 3, 6, 15, 9, 0, 0, 6, 12, 10, 11, 1, 7, 13, 13, 8,
15, 9, 1, 4, 3, 5, 14, 11, 5, 12, 2, 7, 8, 2, 4, 14 },
{ 2, 14, 12, 11, 4, 2, 1, 12, 7, 4, 10, 7, 11, 13, 6, 1,
8, 5, 5, 0, 3, 15, 15, 10, 13, 3, 0, 9, 14, 8, 9, 6,
4, 11, 2, 8, 1, 12, 11, 7, 10, 1, 13, 14, 7, 2, 8, 13,
15, 6, 9, 15, 12, 0, 5, 9, 6, 10, 3, 4, 0, 5, 14, 3 },
{ 12, 10, 1, 15, 10, 4, 15, 2, 9, 7, 2, 12, 6, 9, 8, 5,
0, 6, 13, 1, 3, 13, 4, 14, 14, 0, 7, 11, 5, 3, 11, 8,
9, 4, 14, 3, 15, 2, 5, 12, 2, 9, 8, 5, 12, 15, 3, 10,
7, 11, 0, 14, 4, 1, 10, 7, 1, 6, 13, 0, 11, 8, 6, 13 },
{ 4, 13, 11, 0, 2, 11, 14, 7, 15, 4, 0, 9, 8, 1, 13, 10,
3, 14, 12, 3, 9, 5, 7, 12, 5, 2, 10, 15, 6, 8, 1, 6,
1, 6, 4, 11, 11, 13, 13, 8, 12, 1, 3, 4, 7, 10, 14, 7,
10, 9, 15, 5, 6, 0, 8, 15, 0, 14, 5, 2, 9, 3, 2, 12 },
{ 13, 1, 2, 15, 8, 13, 4, 8, 6, 10, 15, 3, 11, 7, 1, 4,
10, 12, 9, 5, 3, 6, 14, 11, 5, 0, 0, 14, 12, 9, 7, 2,
7, 2, 11, 1, 4, 14, 1, 7, 9, 4, 12, 10, 14, 8, 2, 13,
0, 15, 6, 12, 10, 9, 13, 0, 15, 3, 3, 5, 5, 6, 8, 11 }
};
注意:sbox是一个二维数组,行为8,列为64; 其中列是6bit的索引值检索的。比如:
48bit的值为:101100 000011 110000 010100 001101 000110 001101 110000
也就是索引分别为:44 3 48 20 13 6 13 48
得到的数字为:找到sbox[0][44]为2,则输出的第一个字节的高4bit为2; 找到sbox[1][3]为6,则输出第一个字节的低4bit为6等等,最终组成一个4个字节(32bit)的输出。
- 经过上面的替换之后,输入块需要经过最后一次置换操作。置换表如下所示:
static const int p_table[] = { 16, 7, 20, 21,
29, 12, 28, 17,
1, 15, 23, 26,
5, 18, 31, 10,
2, 8, 24, 14,
32, 27, 3, 9,
19, 13, 30, 6,
22, 11, 4, 25 };
这个操作是对输入的右半部分进行的,做完这个操作之后,对结果和输入的左半部分进行XOR,然后得到的结果成为新的右半部分;在传输之前,原来的右半部分最为新的左半部分。
- 最后,完整的DES加密实现算法如下:
#defineDES_BLOCK_SIZE 8 // 64 bits, DES标准中定义的
#defineDES_KEY_SIZE 8 // 只使用了56bit,但是必须提供8个字节(其余8bit被忽略,见上文)
#defineEXPANSION_BLOCK_SIZE 6 //从32bit扩展到48bit,见上面的描述
#definePC1_KEY_SIZE 7// 最终使用了key的56bit
#defineSUBKEY_SIZE 6 //subkey都是48bit的
//plaintext:需要加密的数据,8个字节; ciphertext:加密后的密文,8个字节;key:密钥,8个字节
static void des_block_operate( const unsigned char plaintext[ DES_BLOCK_SIZE ],
unsigned char ciphertext[ DES_BLOCK_SIZE ],
const unsigned char key[DES_KEY_SIZE ] )
{
// 存储空间;从明文到密文之间经过的结果;不过为了提升性能可以复用这些空间
unsigned char ip_block[DES_BLOCK_SIZE ];
unsigned char expansion_block[ EXPANSION_BLOCK_SIZE ];
unsigned char substitution_block[ DES_BLOCK_SIZE / 2 ];
unsigned char pbox_target[ DES_BLOCK_SIZE / 2 ];
unsigned char recomb_box[ DES_BLOCK_SIZE / 2 ];
unsigned char pc1key[PC1_KEY_SIZE ];
unsigned char subkey[SUBKEY_SIZE ];
int round;
// 进行初始置换
permute(ip_block, plaintext,ip_table, DES_BLOCK_SIZE );
//64bit的key转换位56bit(2个28bit组成)的keyschedule
permute(pc1key, key,pc1_table, PC1_KEY_SIZE );
for ( round= 0; round< 16; round++ )
{
// “Feistel function” on the firsthalf of the block in ‘ip_block’
// “Expansion”. This permutation onlylooks at the first
// four bytes (32 bits of ip_block);16 of these are repeated
// in “expansion_table”.
permute(expansion_block, ip_block + 4, expansion_table, 6 );
// “Key mixing”
// rotate both halves of the initialkey
rol(pc1key );
if ( !(round <= 1 ||round == 8 ||round == 15 ) )
{
// Rotate twice except in rounds 1, 2,9 & 16
rol(pc1key );
}
permute(subkey, pc1key,pc2_table, SUBKEY_SIZE );
xor(expansion_block, subkey, 6 );
// Substitution; “copy” from updatedexpansion block to ciphertext block
memset( ( void* ) substitution_block, 0, DES_BLOCK_SIZE / 2 );
substitution_block[ 0 ] =
sbox[ 0 ][( expansion_block[ 0 ]& 0xFC ) >> 2 ] << 4;
substitution_block[ 0 ]|=
sbox[ 1 ][( expansion_block[ 0 ]& 0x03 ) << 4 |
( expansion_block[ 1 ] & 0xF0 ) >> 4 ];
substitution_block[ 1 ] =
sbox[ 2 ][( expansion_block[ 1 ]& 0x0F ) << 2 |
( expansion_block[ 2 ] & 0xC0 ) >> 6 ] << 4;
substitution_block[ 1 ]|=
sbox[ 3 ][( expansion_block[ 2 ]& 0x3F ) ];
substitution_block[ 2 ] =
sbox[ 4 ][( expansion_block[ 3 ]& 0xFC ) >> 2 ] << 4;
substitution_block[ 2 ]|=
sbox[ 5 ][( expansion_block[ 3 ]& 0x03 ) << 4 |
( expansion_block[ 4 ] & 0xF0 ) >> 4 ];
substitution_block[ 3 ] =
sbox[ 6 ][( expansion_block[ 4 ]& 0x0F ) << 2 |
( expansion_block[ 5 ] & 0xC0 ) >> 6 ] << 4;
substitution_block[ 3 ]|=
sbox[ 7 ][( expansion_block[ 5 ]& 0x3F ) ];
// Permutation
permute(pbox_target, substitution_block, p_table, DES_BLOCK_SIZE / 2 );
// Recombination. XOR the pbox withleft half and then switch sides.
memcpy( ( void* ) recomb_box, ( void *) ip_block, DES_BLOCK_SIZE / 2 );
memcpy( ( void* ) ip_block, ( void* ) ( ip_block + 4),
DES_BLOCK_SIZE/ 2 );
xor(recomb_box, pbox_target, DES_BLOCK_SIZE / 2 );
memcpy( ( void* ) ( ip_block + 4), ( void * )recomb_box,
DES_BLOCK_SIZE/ 2 );
}
// Swap one last time
memcpy( ( void* ) recomb_box, ( void *) ip_block, DES_BLOCK_SIZE / 2 );
memcpy( ( void* ) ip_block, ( void* ) ( ip_block + 4), DES_BLOCK_SIZE / 2 );
memcpy( ( void* ) ( ip_block + 4), ( void * )recomb_box,
DES_BLOCK_SIZE/ 2 );
// Final permutation (undo initialpermutation)
permute(ciphertext, ip_block,fp_table, DES_BLOCK_SIZE );
}
DES解密算法
- DES描述的方式有一个很好的地方是它的解密和加密是一样的,只有key schedule是相反的。在加密的每一轮中,对key是做左轮换;但是在解密时做的是右轮换。其它的都是相似的。我们很容易地对des_block_operate函数增加解密支持,如下面的代码所示:
typedef enum {OP_ENCRYPT, OP_DECRYPT } op_type;
static void des_block_operate( const unsigned char plaintext[ DES_BLOCK_SIZE ],
unsigned char ciphertext[ DES_BLOCK_SIZE ],
const unsigned char key[ DES_KEY_SIZE ],
op_type operation )
{
…
for ( round= 0; round< 16; round++ )
{
permute(expansion_block, ip_block + 4, expansion_table, 6 );
// “Key mixing”
// rotate both halves of the initialkey
if (operation == OP_ENCRYPT )
{
rol(pc1key );
if ( !(round <= 1 ||round == 8 ||round == 15 ) )
{
// Rotate twice except in rounds 1, 2,9 & 16
rol(pc1key );
}
}
permute(subkey, pc1key,pc2_table, SUBKEY_SIZE );
if (operation == OP_DECRYPT )
{
ror(pc1key );
if ( !(round >= 14 ||round == 7 ||round == 0 ) )
{
// Rotate twice except in rounds 1, 2,9 & 16
ror(pc1key );
}
}
xor(expansion_block, subkey, 6 );
...
}
ror的代码如下:
static void ror(unsignedchar *target )
{
int carry_left, carry_right;
carry_right= ( target[ 6 ] & 0x01 ) << 3;
target[ 6 ] =( target[ 6 ]>> 1 ) | ( ( target[5 ] & 0x01 ) << 7 );
target[ 5 ] =( target[ 5 ]>> 1 ) | ( ( target[4 ] & 0x01 ) << 7 );
target[ 4 ] =( target[ 4 ]>> 1 ) | ( ( target[3 ] & 0x01 ) << 7 );
carry_left= ( target[ 3 ] & 0x10 ) << 3;
target[ 3 ] =( ( ( target[ 3 ]>> 1 ) |
( ( target[2 ] & 0x01 ) << 7 ) ) & ~0x08 ) |carry_right;
target[ 2 ] =( target[ 2 ]>> 1 ) | ( ( target[1 ] & 0x01 ) << 7 );
target[ 1 ] =( target[ 1 ]>> 1 ) | ( ( target[0 ] & 0x01 ) << 7 );
target[ 0 ] =( target[ 0 ]>> 1 ) | carry_left;
}
块加密算法中的填充和分组
- 正如前面展示的,DES是对8个字节的块进行操作的。如果输入的字节长度大于8个字节,那么需要反复调用上面的 des_block_operate函数。如果输入没有按照8个字节对齐,那就得对输入进行填充。当然,填充的方案必须按照一定的约定,否则各种实现就不通用了。如果我们采用的传统的方式在后面加0,那我们就需要一种方式来确定输入是否真的是以0结尾还是这些0是填充的。NIST发布了800-38A ( http://csrc.nist.gov/publications/nistpubs/800-38a/sp800-38a.pdf )建议在输入的末尾填充bit 1,然后再后面跟上足够的0,使得输入时8字节对齐的。也就是说,如果输入不是8字节对齐的,我们需要在输入后面先增加一个128的字节(0x80),然后后续跟上足够多的值为0的字节。这样在解密的时候,我们对解密后的结果,从末尾开始,如果为0则删除,直到碰上了值为128的字节。比如:如果输入的是abcdef,为了使它成为8字节,填充之后的结果为:61 62 63 64 65 66 80 00【61为a的ascii值,其它类推】。
- 但是上述方式存在一个问题,如果输入就是8字节对齐的,并且是以0x80后跟0x00结尾时,我们在解密的时候会错误删除字节了。因此,当输入时8字节对齐的时候,我们需要填充一个8字节的块(0x80 0x0 0x0 0x0 0x0 0x0 0x0 0x0)。
- 现在我们就可以来实现 des_encrypt方法,它在对输入填充之后使用 了des_block_operate方法来进行加密。
static void des_operate( const unsigned char *input,
int input_len,
unsigned char *output,
const unsigned char *key,
op_typeoperation )
{
unsigned char input_block[ DES_BLOCK_SIZE ];
assert( !(input_len % DES_BLOCK_SIZE ) );
while (input_len )
{
memcpy( ( void* ) input_block, ( void *) input, DES_BLOCK_SIZE );
des_block_operate( input_block, output, key, operation );
input+= DES_BLOCK_SIZE;
output+= DES_BLOCK_SIZE;
input_len-= DES_BLOCK_SIZE;
}
}
des_encrypt方法如下所示:
void des_encrypt( const unsigned char *plaintext,
const int plaintext_len,
unsigned char *ciphertext,
const unsigned char *key )
{
unsigned char *padded_plaintext;
int padding_len;
// First, pad the input to a multipleof DES_BLOCK_SIZE
padding_len= DES_BLOCK_SIZE - ( plaintext_len %DES_BLOCK_SIZE );
padded_plaintext= malloc(plaintext_len + padding_len );
// This implements NIST 800-3A padding
memset(padded_plaintext, 0x0,plaintext_len + padding_len );
padded_plaintext[ plaintext_len ] = 0x80;
memcpy(padded_plaintext, plaintext,plaintext_len );
des_operate( padded_plaintext, plaintext_len + padding_len, ciphertext, key, OP_ENCRYPT );
free(padded_plaintext );
}
- 除了上面说的NIST 800-38A填充的方法,还有一种填充方法是:PKCS #5 ,它填充的值是需要填充的字节数。这种方式只需要看解密后的最后一个字节的值,然后删除对应数目的字节就可以了。比如:输入的是abcdef,填充之后就是:
6162 63 64 65 66 02 02
a b c d e f
因为需要填充2个字节,所以填充的值为2. 如果输入是8字节对齐 的,那么就增加:0x08 0x08 0x08 0x08 0x08 0x08 0x08 0x08
使用PKCS #5 填充方案,des_encrypt的实现如下:
// First, pad the inputto a multiple of DES_BLOCK_SIZE
padding_len = DES_BLOCK_SIZE - (plaintext_len % DES_BLOCK_SIZE );
padded_plaintext = malloc( plaintext_len + padding_len );
// This implements PKCS#5 padding.
memset( padded_plaintext,padding_len, plaintext_len + padding_len );
memcpy( padded_plaintext,plaintext, plaintext_len );
des_operate( padded_plaintext,plaintext_len + padding_len, ciphertext, key, OP_ENCRYPT );