[从头学数学] 第224节 带着计算机去高考(十六)
[机器小伟]在[工程师阿伟]的陪同下进入了[九转金丹]之第八转的修炼。设想一个场景:
如果允许你带一台不连网的计算机去参加高考,你会放弃选择一个手拿计算器和草稿本吗
?阿伟决定和小伟来尝试一下用计算机算高考题会是怎样的感觉。
正剧开始:
星历2016年05月26日 16:49:14, 银河系厄尔斯星球中华帝国江南行省。
[工程师阿伟]正在和[机器小伟]一起做着2015年的江苏省数学高考题]。
这一节是是[工程师阿伟]带着[机器小伟]去怀旧高考的收关节点。
所以多少会做几个题来表表心意。
这一年的题难度并不高,大部分很简单,只有少数几个难题撑撑门面,
阿伟给评为5.0环难度,比前几年都要低。
说到高考,重新看了这么多年的高考题,阿伟确立了自己的观点:高考题其实是以调戏大家为目的的。
事实上,这些题在生产、生活中很少有真正派上用场的,也就是说,到了现实生活,你会用其它办法去
获取你需要的数据,而不会有人给自己下套来这样调戏自己的。
打个比方,如果你有5个苹果,又买了4个,你有几个苹果?这个题很简单,生活中经常会需要类似的计算。
但到了高考场上卷子会怎样问你,它会这样问:你原来有的苹果数在x=5和y =3的交点上,现在又买了直线
y = x到直线y = x+4*2^[0.5]的距离的苹果,请问你现在有几个苹果啊?
看出来了吧,这就是调戏,你说实际生活中谁会这样玩。
很多人经受不住这种调戏,崩溃了,从而一生都畏惧数学,但其实,真实的数学是很善意的,并且很有用。
到了今年,据说高考又是一次大改革了,反正就像七年之痒一样,每隔几年都要折腾一下,不去管它啦。
如果你恰巧是今年要参加这种调戏试炼的道友,又恰巧来看到了这篇博文,那阿伟就在此提醒一句,
看完这篇,从下一篇开始就不要看了,因为[机器小伟]即将进入元婴期修炼,而后面的知识是不适合结丹期
道友们修习的。
事实上阿伟倾向于建议:在接下来几日内,保持头脑清醒,清心少欲,让自己的状态达到巅峰境界,多集几段气,
憋几个必杀技,没准到时候就能让自己能多冲个一环半环难度的,也是好几十分的出入。
好了,扯了这么多,还是贴题吧,毕竟,阿伟觉得高考已经人过中年了,正逐渐的日薄西山,以后也不会再看它了。
<span style="font-size:18px;">#题1
def tmp1():
A = set([1,2,3]);
B = set([2,4, 5]);
res = A | B;
print(res, len(res));
>>>
{1, 2, 3, 4, 5} 5</span>
<span style="font-size:18px;">#题2
def tmp2():
A = [4, 6, 5, 8, 7, 6];
print(sum(A)/len(A));
>>>
6.0
</span>
<span style="font-size:18px;">#题3
def tmp3():
z = (3+4j)**0.5;
print(abs(z));
>>>
2.23606797749979</span>
<span style="font-size:18px;">#题4
def tmp4():
S, I = 1, 1;
while I < 8:
S += 2;
I += 3;
print(S)
>>>
7</span>

<span style="font-size:18px;">#题8
def tmp8():
a = math.atan(-2);
ab = math.atan(1/7);
print(math.tan(ab-a));
>>>
3.0</span>
<span style="font-size:18px;">#题11
def tmp11():
a_1 = 1;
a = [];
a.append(a_1);
for i in range(1, 11):
a.append(a[-1]+i+1);
sum_ = 0;
for i in range(len(a)):
sum_ += 1/a[i];
print(a);
print(sum_);
>>>
[1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66]
1.8333333333333333
>>> 20/11
1.8181818181818181
</span>
这个题是个什么意思,阿伟觉得理解不能了。求了一下两个曲线的交点
<span style="font-size:18px;">>>>
step1: ['(1)*x', '(-1)*y', '(1)']
step1: ['(1)*x^[2]', '(-1)*y^[2]', '(-1)']
[['A_[1]', 0], ['B_[1]', 0], ['C_[1]', 0], ['D_[1]', 1], ['E_[1]', -1], ['F_[1]', 1], ['A_[2]', 1], ['B_[2]', 0], ['C_[2]', -1], ['D_[2]', 0], ['E_[2]', 0], ['F_[2]', -1]]
系数数组: [-2.0, -2.0]
解: [-1.]
step1: ['(1)*x', '(-1)*y', '(1)']
step1: ['(1)*x^[2]', '(-1)*y^[2]', '(-1)']
step2: ['(-1)', '(1)*x+(1)']
step2: ['(-1)', '0', '(1)*x^[2]+(-1)']
step3: ['((1)*x+(1))/((-((-1))))']
step3: ['(((((-4)*(((-1))*((1)*x^[2]+(-1)))))^[0.5]))/((2)*((-1)))', '((-((((-4)*(((-1))*((1)*x^[2]+(-1)))))^[0.5])))/((2)*((-1)))']
[[-1.0, 0.0]]
[[-1.0, -0.0]]
step4:
相交点:[-1.0, 0.0]
def tmp12():
solve = StringAlgSolve();
#一次方程
function_1 = alg.strformat(['x', '-y', '1']);
#二次方程
function_2 = alg.strformat(['x^[2]', '-y^[2]', '-1']);
print('step1: ', function_1);
print('step1: ', function_2);
valMap = solve.coefFill([function_1, function_2]);
print(valMap);
#解出的x的根
roots = solve.solveEquationExp2_2(valMap);
#两个方程
f = function_1;
print('step1: ', f);
g = function_2;
print('step1: ', g);
#以下部分是定式,可以不加改动
poly_y_f = solve.coefArray(f, 'y');
print('step2: ', poly_y_f);
poly_y_g = solve.coefArray(g, 'y');
print('step2: ', poly_y_g);
#求方程式<1>的y关于x的表达式
expr_y_root = solve.solvePoly(poly_y_f);
print('step3: ', expr_y_root);
expr_y_root2 = solve.solvePoly(poly_y_g);
print('step3: ', expr_y_root2);
#求相交点的坐标对组
points = [];
points2 = [];
for i in range(len(roots)):
real = abs(roots[i].real);
abs_ = abs(roots[i]);
#实数根
if abs(real-abs_) < 0.001:
for j in range(len(expr_y_root)):
x = roots[i].real;
y = solve.strEval(expr_y_root[j], 'x', x);
points.append([x, y]);
y = solve.strEval(expr_y_root2[j], 'x', x);
points2.append([x, y]);
print(points);
print(points2);
print('step4: ');
for i in range(len(points)):
if (abs(points[i][0]-points2[i][0]) < 1e-3 and abs(points[i][1]-points2[i][1])<1e-3):
print('相交点:[{0}, {1}]'.format(round(points[i][0], 3), round(points[i][1], 3)));
</span>
![[从头学数学] 第224节 带着计算机去高考(十六)_第2张图片](http://img.e-com-net.com/image/info5/2086bbff25fd4bd59dfbe2509f85429f.jpg)
<span style="font-size:18px;">>>> [1.0, 1.0] [0.8660254037844387, 1.3660254037844386] [0.5000000000000001, 1.3660254037844388] [6.123233995736766e-17, 1.0] [-0.4999999999999998, 0.36602540378443893] [-0.8660254037844387, -0.36602540378443876] [-1.0, -0.9999999999999999] [-0.8660254037844388, -1.3660254037844386] [-0.5000000000000004, -1.3660254037844388] [-1.8369701987210297e-16, -1.0000000000000002] [0.5000000000000001, -0.3660254037844385] [0.8660254037844384, 0.36602540378443793] ----- 15.588457268119898 >>> 9*1.732 15.588 </span>
![[从头学数学] 第224节 带着计算机去高考(十六)_第3张图片](http://img.e-com-net.com/image/info5/6f32986ae226492292d6460d9bec1836.jpg)
<span style="font-size:18px;">#题15
def tmp15():
Tri_ABC = geo.solveTriangle(['?', 3, 2, 60, '?', '?']);
BC = Tri_ABC[0];
C = Tri_ABC[5];
print('BC = {0}, sin2C = {1}'.format(BC, math.sin(2*C/180*math.pi)));
>>>
BC = 2.6457513110645903, sin2C = 0.989743318610787
>>> 7**0.5
2.6457513110645907
>>> 4*3**0.5/7
0.989743318610787
</span>
![[从头学数学] 第224节 带着计算机去高考(十六)_第4张图片](http://img.e-com-net.com/image/info5/f7a28af07c1048d7a263750769a990c5.jpg)
试卷贴完了,下面还是贴一下关于解二元二次方程组的后续补充吧。
上一节的解决方案不够全面,还没有考虑到一次式和二次式的交点,以及一次式的交点。
下面进行了补全。
来看一下两个椭圆交点的测试:
<span style="font-size:18px;">def tmp9():
solve = StringAlgSolve();
#椭圆方程
function_1 = alg.strformat(['1/16x^[2]', '1/4y^[2]', '-1']);
#椭圆方程
function_2 = alg.strformat(['1/4x^[2]', '1/16y^[2]', '-1']);
print('step1: ', function_1);
print('step1: ', function_2);
valMap = solve.coefFill([function_1, function_2]);
print(valMap);
#解出的x的根
roots = solve.solveEquationExp2_2(valMap);
#两个方程
f = function_1;
print('step1: ', f);
g = function_2;
print('step1: ', g);
#以下部分是定式,可以不加改动
poly_y_f = solve.coefArray(f, 'y');
print('step2: ', poly_y_f);
poly_y_g = solve.coefArray(g, 'y');
print('step2: ', poly_y_g);
#求方程式<1>的y关于x的表达式
expr_y_root = solve.solvePoly(poly_y_f);
print('step3: ', expr_y_root);
expr_y_root2 = solve.solvePoly(poly_y_g);
print('step3: ', expr_y_root2);
#求相交点的坐标对组
points = [];
points2 = [];
for i in range(len(roots)):
real = abs(roots[i].real);
abs_ = abs(roots[i]);
#实数根
if abs(real-abs_) < 0.001:
for j in range(len(expr_y_root)):
x = roots[i].real;
y = solve.strEval(expr_y_root[j], 'x', x);
points.append([x, y]);
y = solve.strEval(expr_y_root2[j], 'x', x);
points2.append([x, y]);
print(points);
print(points2);
print('step4: ');
for i in range(len(points)):
if (abs(points[i][0]-points2[i][0]) < 1e-3 and abs(points[i][1]-points2[i][1])<1e-3):
print('相交点:[{0}, {1}]'.format(round(points[i][0], 3), round(points[i][1], 3)));</span>
结果:
<span style="font-size:18px;">>>> step1: ['(1/16)*x^[2]', '(1/4)*y^[2]', '(-1)'] step1: ['(1/4)*x^[2]', '(1/16)*y^[2]', '(-1)'] [['A_[1]', 0.0625], ['B_[1]', 0], ['C_[1]', 0.25], ['D_[1]', 0], ['E_[1]', 0], ['F_[1]', -1], ['A_[2]', 0.25], ['B_[2]', 0], ['C_[2]', 0.0625], ['D_[2]', 0], ['E_[2]', 0], ['F_[2]', -1]] 系数数组: [0.054932, 0, -0.351562, 0, 0.5625] 解: [-1.78884936+0.00274031j -1.78884936-0.00274031j 1.78884936+0.00274031j 1.78884936-0.00274031j] step1: ['(1/16)*x^[2]', '(1/4)*y^[2]', '(-1)'] step1: ['(1/4)*x^[2]', '(1/16)*y^[2]', '(-1)'] step2: ['(1/4)', '0', '(1/16)*x^[2]+(-1)'] step2: ['(1/16)', '0', '(1/4)*x^[2]+(-1)'] step3: ['(((((-4)*(((1/4))*((1/16)*x^[2]+(-1)))))^[0.5]))/((2)*((1/4)))', '((-((((-4)*(((1/4))*((1/16)*x^[2]+(-1)))))^[0.5])))/((2)*((1/4)))'] step3: ['(((((-4)*(((1/16))*((1/4)*x^[2]+(-1)))))^[0.5]))/((2)*((1/16)))', '((-((((-4)*(((1/16))*((1/4)*x^[2]+(-1)))))^[0.5])))/((2)*((1/16)))'] [[-1.7888493573300557, 1.7888556381650844], [-1.7888493573300557, -1.7888556381650844], [-1.7888493573300557, 1.7888556381650844], [-1.7888493573300557, -1.7888556381650844], [1.7888493573300579, 1.7888556381650844], [1.7888493573300579, -1.7888556381650844], [1.7888493573300579, 1.7888556381650844], [1.7888493573300579, -1.7888556381650844]] [[-1.7888493573300557, 1.788874480538024], [-1.7888493573300557, -1.788874480538024], [-1.7888493573300557, 1.788874480538024], [-1.7888493573300557, -1.788874480538024], [1.7888493573300579, 1.788874480538024], [1.7888493573300579, -1.788874480538024], [1.7888493573300579, 1.788874480538024], [1.7888493573300579, -1.788874480538024]] step4: 相交点:[-1.789, 1.789] 相交点:[-1.789, -1.789] 相交点:[-1.789, 1.789] 相交点:[-1.789, -1.789] 相交点:[1.789, 1.789] 相交点:[1.789, -1.789] 相交点:[1.789, 1.789] 相交点:[1.789, -1.789] </span>
![[从头学数学] 第224节 带着计算机去高考(十六)_第17张图片](http://img.e-com-net.com/image/info5/ac230972305747f2a10bd10a62c19935.png)
<span style="font-size:18px;"> if (1) {
var r = 20;
config.setSector(1,1,1,1);
config.graphPaper2D(0, 0, r);
config.axis2D(0, 0,180);
//坐标轴设定
var scaleX = 2*r, scaleY = 2*r;
var spaceX = 1, spaceY = 1;
var xS = -10, xE = 10;
var yS = -10, yE = 10;
config.axisSpacing(xS, xE, spaceX, scaleX, 'X');
config.axisSpacing(yS, yE, spaceY, scaleY, 'Y');
var transform = new Transform();
//存放函数图像上的点
var a = [], b = [], c = [], d = [];
//需要显示的函数说明
//希腊字母表(存此用于Ctrl C/V
//ΑΒΓΔΕΖΗΘΙΚΛΜΝΞΟΠΡΣΤΥΦΧΨΩ
//αβγδεζηθικλμνξοπρστυφχψω
var f1 = 'x^[2]/16+y^[2]/4 = 1', f2 = 'x^[2]/4+y^[2]/16 = 1', f3 = '', f4 = '';
//函数描点
//参数方程
var x, y;
var pointA = [];
for (var thita = 0; thita < Math.PI*2; thita +=Math.PI/48) {
x = 4*Math.cos(thita);
y = 2*Math.sin(thita);
a.push([x, y]);
x = 2*Math.cos(thita);
y = 4*Math.sin(thita);
b.push([x, y]);
}
//存放临时数组
var tmp = [];
//显示变换
if (a.length > 0) {
a = transform.scale(transform.translate(a, 0, 0), scaleX/spaceX, scaleY/spaceY);
//函数1
tmp = [].concat(a);
shape.pointDraw(tmp, 'red');
tmp = [].concat(a);
shape.multiLineDraw(tmp, 'pink');
plot.setFillStyle('red');
plot.fillText(f1, 100, -90, 200);
}
//显示变换
if (b.length > 0) {
b = transform.scale(transform.translate(b, 0, 0), scaleX/spaceX, scaleY/spaceY);
//函数1
tmp = [].concat(b);
shape.pointDraw(tmp, 'green');
tmp = [].concat(b);
shape.multiLineDraw(tmp, 'green');
plot.setFillStyle('green');
plot.fillText(f2, 100, -120, 200);
}
}</span>
以下是一些中间产物,可忽略:
<span style="font-size:18px;">#如果二元二次方程组退化成二元一次方程组
def tmp11():
print('#如果二元二次方程组退化成二元一次方程组');
#用x来表示y, 消去y元
expr_y = alg.strformat(['-D_[1]E_[1]^[-1]x', '-F_[1]E_[1]^[-1]']);
print('step1: ', expr_y);
#代入第二个代数式
expr_y_2 = alg.strcombine(alg.strformat(['-D_[2]x', '-F_[2]'])+
alg.strdot(alg.strformat(['E_[2]']), expr_y));
print('step2: ', expr_y_2);
#如果二元二次方程组退化成二元一次方程组
step1: ['(-1)*D_[1]*E_[1]^[-1]*x', '(-1)*F_[1]*E_[1]^[-1]']
step2: ['(-1)*D_[2]^[1]*x^[1]', '(-1)*F_[2]^[1]', '(-1)*D_[1]^[1]*E_[1]^[-1]*E_[2]^[1]*x^[1]', '(-1)*E_[1]^[-1]*E_[2]^[1]*F_[1]^[1]']
//一元一次方程组系数(两方程都是一次式)
if (1) {
var mathText = new MathText();
//希腊字母表(存此用于Ctrl C/V
//ΑΒΓΔΕΖΗ ΘΙΚΛΜΝΞ ΟΠΡ ΣΤΥ ΦΧΨ Ω
//αβγδεζη θικλμνξ οπρ στυ φχψ ω
//希腊大小写字母
var GreekCaps = 'ΑΒΓΔΕΖΗΘΙΚΛΜΝΞΟΠΡΣΤΥΦΧΨΩ';
var GreakSmall = 'αβγδεζηθικλμνξοπρστυφχψω';
var s = [
'D_[1]x+E_[1]y+F_[1] = 0 _[(1)]',
'D_[2]x+E_[2]y+F_[2] = 0 _[(2)]',
' 系数阵列',
'(-1)*D_[2]^[1]*x^[1]',
'+(-1)*F_[2]^[1]',
'+(-1)*D_[1]^[1]*E_[1]^[-1]*E_[2]^[1]*x^[1]',
'+(-1)*E_[1]^[-1]*E_[2]^[1]*F_[1]^[1] = 0'
];
var x =40, y=40;
var r1 = 40;
var len = s.length;
for (var i = 0; i < len; i++) {
if (s[i] == '') {
if (x < 100) {
x += 300;
y-=r1*3;
}
else {
x = 20;
y += r1;
}
}
else {
mathText.print(s[i], x, y, 'red', '|');
y+=r1;
}
}
}</span>
<span style="font-size:18px;">#题9
def tmp9():
solve = StringAlgSolve();
#直线方程
function_1 = alg.strformat(['1/16x^[2]', '1/4y^[2]', '-1']);
#圆方程
function_2 = alg.strformat(['1/4x^[2]', '1/16y^[2]', '-1']);
print('step1: ', function_1);
print('step1: ', function_2);
valMap = solve.coefFill([function_1, function_2]);
print(valMap);
#解出的x的根
roots = solve.solveEquationExp2_2(valMap);
#两个方程
f = function_1;
print('step1: ', f);
g = function_2;
print('step1: ', g);
#以下部分是定式,可以不加改动
poly_y_f = solve.coefArray(f, 'y');
print('step2: ', poly_y_f);
poly_y_g = solve.coefArray(g, 'y');
print('step2: ', poly_y_g);
#求方程式<1>的y关于x的表达式
expr_y_root = solve.solvePoly(poly_y_f);
print('step3: ', expr_y_root);
expr_y_root2 = solve.solvePoly(poly_y_g);
print('step3: ', expr_y_root2);
#求相交点的坐标对组
points = [];
points2 = [];
for i in range(len(roots)):
real = abs(roots[i].real);
abs_ = abs(roots[i]);
#实数根
if abs(real-abs_) < 0.001:
for j in range(len(expr_y_root)):
x = roots[i].real;
y = solve.strEval(expr_y_root[j], 'x', x);
points.append([x, y]);
y = solve.strEval(expr_y_root2[j], 'x', x);
points2.append([x, y]);
print(points);
print(points2);
print('step4: ');
for i in range(len(points)):
if (abs(points[i][0]-points2[i][0]) < 1e-3 and abs(points[i][1]-points2[i][1])<1e-3):
print('相交点:[{0}, {1}]'.format(round(points[i][0], 3), round(points[i][1], 3)));
#如果二元二次方程组中有一个不是二次式
def tmp10():
print('#如果二元二次方程组中有一个不是二次式');
#用x来表示y, 消去y元
expr_y = alg.strformat(['-D_[1]E_[1]^[-1]x', '-F_[1]E_[1]^[-1]']);
print('step1: ', expr_y);
#代入第二个代数式
expr_y_2 = alg.strcombine(alg.strformat(['A_[2]x^[2]', 'D_[2]x', 'F_[2]'])+
alg.strdot(alg.strformat(['B_[2]x']), expr_y)+
alg.strdot(alg.strformat(['C_[2]']), alg.strpow_n(expr_y, 2)));
print('step2: ', expr_y_2);
#如果二元二次方程组退化成二元一次方程组
def tmp11():
print('#如果二元二次方程组退化成二元一次方程组');
#用x来表示y, 消去y元
expr_y = alg.strformat(['-D_[1]E_[1]^[-1]x', '-F_[1]E_[1]^[-1]']);
print('step1: ', expr_y);
#代入第二个代数式
expr_y_2 = alg.strcombine(alg.strformat(['-D_[2]x', '-F_[2]'])+
alg.strdot(alg.strformat(['E_[2]']), expr_y));
print('step2: ', expr_y_2);
#测试
def tmp12():
solve = StringAlgSolve();
#直线方程
function_1 = alg.strformat(['x', '1/4y', '-1']);
#圆方程
function_2 = alg.strformat(['1/4x^[2]', '1/16y^[2]', '-1']);
print('step1: ', function_1);
print('step1: ', function_2);
valMap = solve.coefFill([function_1, function_2]);
print(valMap);
#解出的x的根
roots = solve.solveEquationExp2_2(valMap);
#两个方程
f = function_1;
print('step1: ', f);
g = function_2;
print('step1: ', g);
#以下部分是定式,可以不加改动
poly_y_f = solve.coefArray(f, 'y');
print('step2: ', poly_y_f);
poly_y_g = solve.coefArray(g, 'y');
print('step2: ', poly_y_g);
#求方程式<1>的y关于x的表达式
expr_y_root = solve.solvePoly(poly_y_f);
print('step3: ', expr_y_root);
expr_y_root2 = solve.solvePoly(poly_y_g);
print('step3: ', expr_y_root2);
#求相交点的坐标对组
points = [];
points2 = [];
for i in range(len(roots)):
real = abs(roots[i].real);
abs_ = abs(roots[i]);
#实数根
if abs(real-abs_) < 0.001:
for j in range(len(expr_y_root)):
x = roots[i].real;
y = solve.strEval(expr_y_root[j], 'x', x);
points.append([x, y]);
y = solve.strEval(expr_y_root2[j], 'x', x);
points2.append([x, y]);
print(points);
print(points2);
print('step4: ');
for i in range(len(points)):
if (abs(points[i][0]-points2[i][0]) < 1e-3 and abs(points[i][1]-points2[i][1])<1e-3):
print('相交点:[{0}, {1}]'.format(round(points[i][0], 3), round(points[i][1], 3)));
</span>
工具上的增改在这块:
<span style="font-size:18px;"> #解二元二次方程组的第二种方法尝试,最暴力的代入消元法
def solveEquationExp2_2(self, valueMap):
'''
#第一个方程
expr_1 = alg.strformat(['A_[1]x^[2]', 'B_[1]xy', 'C_[1]y^[2]', 'D_[1]x', 'E_[1]y', 'F_[1]']);
#第二个方程
expr_2 = alg.strformat(['A_[2]x^[2]', 'B_[2]xy', 'C_[2]y^[2]', 'D_[2]x', 'E_[2]y', 'F_[2]']);
'''
A_1 = valueMap[0][1];
B_1 = valueMap[1][1];
C_1 = valueMap[2][1];
D_1 = valueMap[3][1];
E_1 = valueMap[4][1];
F_1 = valueMap[5][1];
A_2 = valueMap[6][1];
B_2 = valueMap[7][1];
C_2 = valueMap[8][1];
D_2 = valueMap[9][1];
E_2 = valueMap[10][1];
F_2 = valueMap[11][1];
#消元一次要从二次项y^[2]的系数不为0的那个方程消起,除非某个方程完全没有二次项
#所以第一个方程二次项y^[2]的系数不要为0
#否则应该调换方程顺序
if (C_1 != 0 and C_2 != 0):
#一共63项的关于未知数x的最高四次方的系数矩阵
coefArray = ['(1.0)*A_[2]^[1]*B_[1]^[2]*C_[1]^[-2]*C_[2]^[1]*x^[4]',
'(1.0)*B_[1]^[2]*C_[1]^[-2]*C_[2]^[1]*D_[2]^[1]*x^[3]',
'(1.0)*B_[1]^[2]*C_[1]^[-2]*C_[2]^[1]*F_[2]^[1]*x^[2]',
'(2.0)*A_[2]^[1]*B_[1]^[1]*C_[1]^[-2]*C_[2]^[1]*E_[1]^[1]*x^[3]',
'(2.0)*B_[1]^[1]*C_[1]^[-2]*C_[2]^[1]*D_[2]^[1]*E_[1]^[1]*x^[2]',
'(2.0)*B_[1]^[1]*C_[1]^[-2]*C_[2]^[1]*E_[1]^[1]*F_[2]^[1]*x^[1]',
'(1.0)*A_[2]^[1]*C_[1]^[-2]*C_[2]^[1]*E_[1]^[2]*x^[2]',
'(1.0)*C_[1]^[-2]*C_[2]^[1]*D_[2]^[1]*E_[1]^[2]*x^[1]',
'(1.0)*C_[1]^[-2]*C_[2]^[1]*E_[1]^[2]*F_[2]^[1]',
'(1.0)*A_[1]^[2]*C_[1]^[-2]*C_[2]^[2]*x^[4]',
'(2.0)*A_[1]^[1]*C_[1]^[-2]*C_[2]^[2]*D_[1]^[1]*x^[3]',
'(2.0)*A_[1]^[1]*C_[1]^[-2]*C_[2]^[2]*F_[1]^[1]*x^[2]',
'(-1.0)*A_[1]^[1]*B_[1]^[1]*B_[2]^[1]*C_[1]^[-2]*C_[2]^[1]*x^[4]',
'(-1.0)*A_[1]^[1]*B_[2]^[1]*C_[1]^[-2]*C_[2]^[1]*E_[1]^[1]*x^[3]',
'(-1.0)*A_[1]^[1]*B_[1]^[1]*C_[1]^[-2]*C_[2]^[1]*E_[2]^[1]*x^[3]',
'(-1.0)*A_[1]^[1]*C_[1]^[-2]*C_[2]^[1]*E_[1]^[1]*E_[2]^[1]*x^[2]',
'(-2.0)*A_[1]^[1]*A_[2]^[1]*C_[1]^[-1]*C_[2]^[1]*x^[4]',
'(-2.0)*A_[1]^[1]*C_[1]^[-1]*C_[2]^[1]*D_[2]^[1]*x^[3]',
'(-2.0)*A_[1]^[1]*C_[1]^[-1]*C_[2]^[1]*F_[2]^[1]*x^[2]',
'(1.0)*C_[1]^[-2]*C_[2]^[2]*D_[1]^[2]*x^[2]',
'(2.0)*C_[1]^[-2]*C_[2]^[2]*D_[1]^[1]*F_[1]^[1]*x^[1]',
'(-1.0)*B_[1]^[1]*B_[2]^[1]*C_[1]^[-2]*C_[2]^[1]*D_[1]^[1]*x^[3]',
'(-1.0)*B_[2]^[1]*C_[1]^[-2]*C_[2]^[1]*D_[1]^[1]*E_[1]^[1]*x^[2]',
'(-1.0)*B_[1]^[1]*C_[1]^[-2]*C_[2]^[1]*D_[1]^[1]*E_[2]^[1]*x^[2]',
'(-1.0)*C_[1]^[-2]*C_[2]^[1]*D_[1]^[1]*E_[1]^[1]*E_[2]^[1]*x^[1]',
'(-2.0)*A_[2]^[1]*C_[1]^[-1]*C_[2]^[1]*D_[1]^[1]*x^[3]',
'(-2.0)*C_[1]^[-1]*C_[2]^[1]*D_[1]^[1]*D_[2]^[1]*x^[2]',
'(-2.0)*C_[1]^[-1]*C_[2]^[1]*D_[1]^[1]*F_[2]^[1]*x^[1]',
'(1.0)*C_[1]^[-2]*C_[2]^[2]*F_[1]^[2]',
'(-1.0)*B_[1]^[1]*B_[2]^[1]*C_[1]^[-2]*C_[2]^[1]*F_[1]^[1]*x^[2]',
'(-1.0)*B_[2]^[1]*C_[1]^[-2]*C_[2]^[1]*E_[1]^[1]*F_[1]^[1]*x^[1]',
'(-1.0)*B_[1]^[1]*C_[1]^[-2]*C_[2]^[1]*E_[2]^[1]*F_[1]^[1]*x^[1]',
'(-1.0)*C_[1]^[-2]*C_[2]^[1]*E_[1]^[1]*E_[2]^[1]*F_[1]^[1]',
'(-2.0)*A_[2]^[1]*C_[1]^[-1]*C_[2]^[1]*F_[1]^[1]*x^[2]',
'(-2.0)*C_[1]^[-1]*C_[2]^[1]*D_[2]^[1]*F_[1]^[1]*x^[1]',
'(-2.0)*C_[1]^[-1]*C_[2]^[1]*F_[1]^[1]*F_[2]^[1]',
'(-1.0)*A_[2]^[1]*B_[1]^[1]*B_[2]^[1]*C_[1]^[-1]*x^[4]',
'(-1.0)*B_[1]^[1]*B_[2]^[1]*C_[1]^[-1]*D_[2]^[1]*x^[3]',
'(-1.0)*B_[1]^[1]*B_[2]^[1]*C_[1]^[-1]*F_[2]^[1]*x^[2]',
'(-1.0)*A_[2]^[1]*B_[2]^[1]*C_[1]^[-1]*E_[1]^[1]*x^[3]',
'(-1.0)*B_[2]^[1]*C_[1]^[-1]*D_[2]^[1]*E_[1]^[1]*x^[2]',
'(-1.0)*B_[2]^[1]*C_[1]^[-1]*E_[1]^[1]*F_[2]^[1]*x^[1]',
'(-1.0)*A_[2]^[1]*B_[1]^[1]*C_[1]^[-1]*E_[2]^[1]*x^[3]',
'(-1.0)*B_[1]^[1]*C_[1]^[-1]*D_[2]^[1]*E_[2]^[1]*x^[2]',
'(-1.0)*B_[1]^[1]*C_[1]^[-1]*E_[2]^[1]*F_[2]^[1]*x^[1]',
'(-1.0)*A_[2]^[1]*C_[1]^[-1]*E_[1]^[1]*E_[2]^[1]*x^[2]',
'(-1.0)*C_[1]^[-1]*D_[2]^[1]*E_[1]^[1]*E_[2]^[1]*x^[1]',
'(-1.0)*C_[1]^[-1]*E_[1]^[1]*E_[2]^[1]*F_[2]^[1]',
'(1)*A_[2]^[2]*x^[4]',
'(2)*A_[2]^[1]*D_[2]^[1]*x^[3]',
'(2)*A_[2]^[1]*F_[2]^[1]*x^[2]',
'(1)*D_[2]^[2]*x^[2]',
'(2)*D_[2]^[1]*F_[2]^[1]*x^[1]',
'(1)*F_[2]^[2]',
'(1.0)*A_[1]^[1]*B_[2]^[2]*C_[1]^[-1]*x^[4]',
'(1.0)*B_[2]^[2]*C_[1]^[-1]*D_[1]^[1]*x^[3]',
'(1.0)*B_[2]^[2]*C_[1]^[-1]*F_[1]^[1]*x^[2]',
'(2.0)*A_[1]^[1]*B_[2]^[1]*C_[1]^[-1]*E_[2]^[1]*x^[3]',
'(2.0)*B_[2]^[1]*C_[1]^[-1]*D_[1]^[1]*E_[2]^[1]*x^[2]',
'(2.0)*B_[2]^[1]*C_[1]^[-1]*E_[2]^[1]*F_[1]^[1]*x^[1]',
'(1.0)*A_[1]^[1]*C_[1]^[-1]*E_[2]^[2]*x^[2]',
'(1.0)*C_[1]^[-1]*D_[1]^[1]*E_[2]^[2]*x^[1]',
'(1.0)*C_[1]^[-1]*E_[2]^[2]*F_[1]^[1]']; #这整个是一个和为零的多项式
#如果某一个方程没有二次项,适用这套系数
elif (C_1 == 0 and B_1 == 0 and A_1 == 0):
if (E_1 != 0):
coefArray = ['(1)*A_[2]^[1]*x^[2]',
'(1)*D_[2]^[1]*x^[1]',
'(1)*F_[2]^[1]',
'(-1)*B_[2]^[1]*D_[1]^[1]*E_[1]^[-1]*x^[2]',
'(-1)*B_[2]^[1]*E_[1]^[-1]*F_[1]^[1]*x^[1]',
'(1)*C_[2]^[1]*D_[1]^[2]*E_[1]^[-2]*x^[2]',
'(2)*C_[2]^[1]*D_[1]^[1]*E_[1]^[-2]*F_[1]^[1]*x^[1]',
'(1)*C_[2]^[1]*E_[1]^[-2]*F_[1]^[2]'];
else:
print('无穷多解或无解。');
return [];
elif (C_1 == 0 and B_1 == 0 and A_1 == 0 and
C_2 == 0 and B_2 == 0 and A_2 == 0):
if (E_1 != 0):
coefArray = ['(-1)*D_[2]^[1]*x^[1]',
'(-1)*F_[2]^[1]',
'(-1)*D_[1]^[1]*E_[1]^[-1]*E_[2]^[1]*x^[1]',
'(-1)*E_[1]^[-1]*E_[2]^[1]*F_[1]^[1]'];
else:
print('无穷多解或无解。');
return [];
else:
print('或许需要调换位置,保证第一个方程的y^[2]的系数存在,可调换x和y参数实现。');
print('如果两个方程中找不出一个x^[2]或y^[2],则可以考虑消去xy项得一次方程组。');
#赋值系数,应该有12个
len_ = len(valueMap);
size = len(coefArray);
result = [];
for i in range(size):
s = coefArray[i];
#由于字母排序原因,一般x会排在最后,各系数ABCDEF会排在前面,
#这会带来一些方便
index = s.find('x');
if (index != -1):
#系数部分
part1 = s[:index-1];
#参数x部分
part2 = s[index-1:];
else:
part1 = s;
part2 = '';
for j in range(len_):
part1 = part1.replace(valueMap[j][0], '('+str(valueMap[j][1])+')');
part1 = part1.replace('^[', '**(');
part1 = part1.replace(']', ')');
#print(part1);
part1 = '('+str(eval(part1))+')';
result.append(part1+part2);
#print(result);
result = alg.strcombine(result);
#print(result);
coef_x = self.coefPoly(result, 'x');
print('系数数组:', coef_x);
roots = np.roots(coef_x);
print('解: ', roots);
return roots;
#填充二元二次方程组的系数阵列,一共十二个
def coefFill(self, functions, element1 = 'x', element2 = 'y'):
#functions是两个方程的多项式组成的数组[fun1, func2],
#具有格式化后的多项式样式fun1, 2 = [mono1, mono2, ...]
func1 = functions[0];
func2 = functions[1];
if (element1 != 'x'):
for i in range(len(func1)):
func1[i] = func1[i].replace(element1, 'x');
for i in range(len(func2)):
func2[i] = func2[i].replace(element1, 'x');
if (element2 != 'y'):
for i in range(len(func1)):
func1[i] = func1[i].replace(element2, 'y');
for i in range(len(func2)):
func2[i] = func2[i].replace(element2, 'y');
'''
#第一个方程
expr_1 = alg.strformat(['A_[1]x^[2]', 'B_[1]xy', 'C_[1]y^[2]', 'D_[1]x', 'E_[1]y', 'F_[1]']);
#第二个方程
expr_2 = alg.strformat(['A_[2]x^[2]', 'B_[2]xy', 'C_[2]y^[2]', 'D_[2]x', 'E_[2]y', 'F_[2]']);
'''
#用参数值填充,注意按照同类项来填系数
valMap = [['A_[1]', 0], ['B_[1]', 0],['C_[1]', 0],
['D_[1]', 0], ['E_[1]', 0],['F_[1]', 0],
['A_[2]', 0], ['B_[2]', 0],['C_[2]', 0],
['D_[2]', 0], ['E_[2]', 0],['F_[2]', 0]];
coefs = len(valMap);
cycle = 0;
for i in range(len(func1)):
s = func1[i];
xIndex = s.find('x');
yIndex = s.find('y');
if (xIndex != -1):
if (yIndex != -1):
min_ = min(xIndex, yIndex);
else:
min_ = xIndex;
else:
if (yIndex != -1):
min_ = yIndex
else:
min_ = -1;
if (min_ != -1):
#参数式
s_1 = s[min_:];
#系数
s_2 = s[:min_-1];
else:
s_1 = '';
s_2 = s;
if (s_1 == 'x^[2]'):
valMap[0+cycle*6][1] = eval(s_2);
elif (s_1 == 'x^[1]y^[1]' or s_1 == 'xy' ):
valMap[1+cycle*6][1] = eval(s_2);
elif (s_1 == 'y^[2]'):
valMap[2+cycle*6][1] = eval(s_2);
elif (s_1 == 'x^[1]' or s_1 == 'x'):
valMap[3+cycle*6][1] = eval(s_2);
elif (s_1 == 'y^[1]' or s_1 == 'y'):
valMap[4+cycle*6][1] = eval(s_2);
elif (s_1 == ''):
valMap[5+cycle*6][1] = eval(s_2);
cycle = 1;
for i in range(len(func2)):
s = func2[i];
xIndex = s.find('x');
yIndex = s.find('y');
if (xIndex != -1):
if (yIndex != -1):
min_ = min(xIndex, yIndex);
else:
min_ = xIndex;
else:
if (yIndex != -1):
min_ = yIndex
else:
min_ = -1;
if (min_ != -1):
#参数式
s_1 = s[min_:];
#系数
s_2 = s[:min_-1];
else:
s_1 = '';
s_2 = s;
if (s_1 == 'x^[2]'):
valMap[0+cycle*6][1] = eval(s_2);
elif (s_1 == 'x^[1]y^[1]' or s_1 == 'xy' ):
valMap[1+cycle*6][1] = eval(s_2);
elif (s_1 == 'y^[2]'):
valMap[2+cycle*6][1] = eval(s_2);
elif (s_1 == 'x^[1]' or s_1 == 'x'):
valMap[3+cycle*6][1] = eval(s_2);
elif (s_1 == 'y^[1]' or s_1 == 'y'):
valMap[4+cycle*6][1] = eval(s_2);
elif (s_1 == ''):
valMap[5+cycle*6][1] = eval(s_2);
return valMap;</span>
现在的工具完整度已经达到可以解80%以上最高次是二次的二元方程组了。
也就是说最多只能是二元,可以是一次,或者二次,并且还没有穷尽所有系数配置。
不过一般来说,应该够用了,至少,所有圆锥曲线,直线这块是没问题了。
可惜只能在平面内,到了空间就是三元了。
看一个直线和椭圆交点的测试:
<span style="font-size:18px;">#测试
def tmp12():
solve = StringAlgSolve();
#直线方程
function_1 = alg.strformat(['x', '1/4y', '-1']);
#圆方程
function_2 = alg.strformat(['1/4x^[2]', '1/16y^[2]', '-1']);
print('step1: ', function_1);
print('step1: ', function_2);
valMap = solve.coefFill([function_1, function_2]);
print(valMap);
#解出的x的根
roots = solve.solveEquationExp2_2(valMap);
#两个方程
f = function_1;
print('step1: ', f);
g = function_2;
print('step1: ', g);
#以下部分是定式,可以不加改动
poly_y_f = solve.coefArray(f, 'y');
print('step2: ', poly_y_f);
poly_y_g = solve.coefArray(g, 'y');
print('step2: ', poly_y_g);
#求方程式<1>的y关于x的表达式
expr_y_root = solve.solvePoly(poly_y_f);
print('step3: ', expr_y_root);
expr_y_root2 = solve.solvePoly(poly_y_g);
print('step3: ', expr_y_root2);
#求相交点的坐标对组
points = [];
points2 = [];
for i in range(len(roots)):
real = abs(roots[i].real);
abs_ = abs(roots[i]);
#实数根
if abs(real-abs_) < 0.001:
for j in range(len(expr_y_root)):
x = roots[i].real;
y = solve.strEval(expr_y_root[j], 'x', x);
points.append([x, y]);
y = solve.strEval(expr_y_root2[j], 'x', x);
points2.append([x, y]);
print(points);
print(points2);
print('step4: ');
for i in range(len(points)):
if (abs(points[i][0]-points2[i][0]) < 1e-3 and abs(points[i][1]-points2[i][1])<1e-3):
print('相交点:[{0}, {1}]'.format(round(points[i][0], 3), round(points[i][1], 3)));
</span>
结果:
这里还是有一点小问题,因为明明是两个交点,却只给出了一个,这个先放着。
本节到此结束,欲知后事如何,请看下回分解。
注:阿伟来预测一下2016年的高考难度:5.5环 难度 概率 80%; 6环难度, 概率10%, 5环难度10%,
诸位道友依据5.5环难度制定应对策略,应该没什么问题,如果碰到变态的6环难度,那就是命不好了。
![[从头学数学] 第224节 带着计算机去高考(十六)_第1张图片](http://img.e-com-net.com/image/info5/923d302e9f774cc295a9a0f3e237d6a1.jpg)




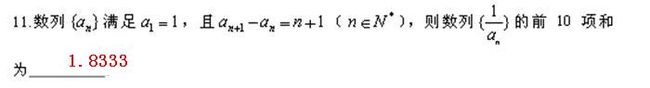
![[从头学数学] 第224节 带着计算机去高考(十六)_第5张图片](http://img.e-com-net.com/image/info5/c699384f2bbd45549619ddc9e9c0400d.jpg)
![[从头学数学] 第224节 带着计算机去高考(十六)_第6张图片](http://img.e-com-net.com/image/info5/d085339985ef4a829f5ea880e69f5972.jpg)
![[从头学数学] 第224节 带着计算机去高考(十六)_第7张图片](http://img.e-com-net.com/image/info5/d230248b26984ea0bba043ebf00d08d2.jpg)
![[从头学数学] 第224节 带着计算机去高考(十六)_第8张图片](http://img.e-com-net.com/image/info5/60caa3fa51ce43af8b0082081e3c7f3f.jpg)
![[从头学数学] 第224节 带着计算机去高考(十六)_第9张图片](http://img.e-com-net.com/image/info5/4b20e2ab1a35483484cf68e7eeb72a8b.jpg)
![[从头学数学] 第224节 带着计算机去高考(十六)_第10张图片](http://img.e-com-net.com/image/info5/fb3f5e174087490d88ec1a61dc897a44.jpg)
![[从头学数学] 第224节 带着计算机去高考(十六)_第11张图片](http://img.e-com-net.com/image/info5/30567eb82f764b9585785f86fa3ad420.jpg)
![[从头学数学] 第224节 带着计算机去高考(十六)_第12张图片](http://img.e-com-net.com/image/info5/5dbbcfa3c8c24ffd9167db0c1e7a2e3b.jpg)
![[从头学数学] 第224节 带着计算机去高考(十六)_第13张图片](http://img.e-com-net.com/image/info5/48b0d2d4a44540f8956224ffb1a1bb35.jpg)
![[从头学数学] 第224节 带着计算机去高考(十六)_第14张图片](http://img.e-com-net.com/image/info5/4a7ec70e4b5847c3ab1f2175dde6051d.jpg)
![[从头学数学] 第224节 带着计算机去高考(十六)_第15张图片](http://img.e-com-net.com/image/info5/bef3930476604712a5ffc580dd91becf.png)
![[从头学数学] 第224节 带着计算机去高考(十六)_第16张图片](http://img.e-com-net.com/image/info5/5c57829f78a742edab92e8360408ed3f.jpg)
![[从头学数学] 第224节 带着计算机去高考(十六)_第18张图片](http://img.e-com-net.com/image/info5/aa9bd27762b64036a9f9dbeed516ef6f.jpg)
![[从头学数学] 第224节 带着计算机去高考(十六)_第19张图片](http://img.e-com-net.com/image/info5/0f70f58e145f4f94ad6a110ae920bb2a.png)