第一章 绪论
1. 贝叶斯概率公式
加法规则: p(X)=∑Yp(X,Y)
乘法规则: p(X,Y)=p(Y|X)p(X)
贝叶斯公式: p(Y|X)=p(X|Y)p(Y)p(X)
2. 用贝叶斯的观点解释多项式拟合
本节对应PRML (Pattern Recognition and Machine Learning)的1.2.5节。给定训练集 x=(x1,x2,…,xN)T ,样本标签 t=(t1,t2,…,tN)T ,可以用一个高斯分布来描述目标值 t 的不确定性。对于多项式拟合来说,我们有
其中 M 是多项式的阶数, xj 是 x 的 j 次幂。拟合误差
按照贝叶斯理论的观点,拟合误差服从均值为 0 方差为 σ2 的高斯分布,记 β=1σ2 ,即 en∼N(0,β−1) 。下图显示了这种描述关系
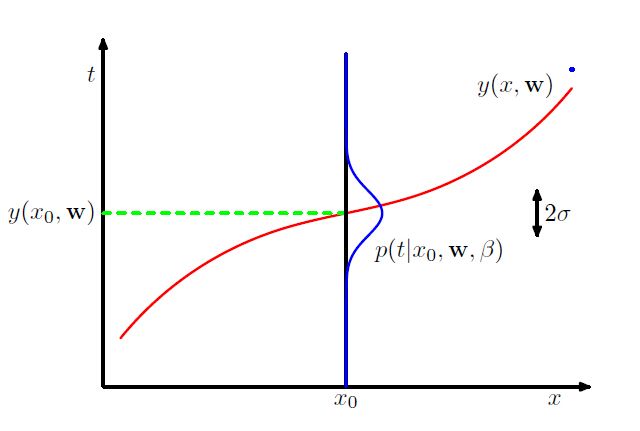
因此训练数据 {x,t} 可以用来估计 x 和 β 的最大似然估计值。似然函数
对似然函数取对数,得
当取 β=1 时,对数似然函数可以简化为
最大化对数函数等价于最小化误差平方和函数,此时与多项式拟合的目标变的一致。当参数 β 不是固定值时,我们精度参数,因为 β 与误差的方差有关,从上图也可以看出。同样,对数似然函数对 β−1 (将 β−1 看成一个整体,而不是一个数的倒数)求偏导,令偏导数等于0,可求得 β−1 的最大似然估计值
其中 wML 是参数 w 的最大似然估计值。
估计出参数 w 和 β 之后,我们可以对测试集中的 x 做预测,并且可以给出预测值等于 t 的概率,这是利用贝叶斯方法估计参数的优点之一。
此时是相对于测试集来说的。
下面用贝叶斯的观点来解释模型参数正则化,来解决过拟合问题。假定多项式系数 w 也服从如下的高斯分布
其中 α 称之为超参数,控制参数 w 的分布。应用贝叶斯定理, w 后验分布正比于先验分布和似然函数的成绩
原因是: p(w|x,t,α,β)=p(w,x,t,α,β)/p(x,t,α,β)=p(t|w,x,α,β)p(w,x,α,β)/p(x,t,α,β) =p(t|w,x,b)p(w|x,β,α)p(x,β,α)/p(x,t,α,β)=p(t|w,x,β)p(w|α)p(x,β,α)/p(x,t,α,β) , α 与 t 无关,故 p(t|w,x,b,α) 中 α 可省略,因为 α 是 w 的超参故 p(w|x,β,α)=p(w|α) 。
通过最大化后验概率(MAP),我们可以估计出所有的参数,其对数似然函数是
上式省略了与参数无关“常数项”。此时相当于正则项的惩罚系数 λ=α/β 。
3. 贝叶斯曲线拟合
前面的分析我们加入了先验分布 p(w|α) ,但是我们对 w 估计任然是点估计,因此还不能将其视为贝叶斯解法。在整套贝叶斯方法下,我们将运用概率的求和法则和乘积法则,对 w 求积分得到关于 w 的边缘分布,这才是模式识别中贝叶斯方法的核心。
在曲线拟合中,我们给定训练集 x 和 t ,估计出模型参数 w ,对于预测集中的点 x ,我们的目标是用这个模型预测出与这个点相对应的目标值 t 。这里我们假定 α 和 β 是固定并且已知的(在后面的章节中我们将讨论如何在贝叶斯的框架下面从训练数据中估计这两个参数)。
我们最终需要在预测集上得到如下的分布
推导过程是:根据贝叶斯求和法则(对连续型变量来说相当于积分) p(t|x,x,t)=∫p(t,w|x,x,t)dw , p(t,w|x,x,t)=p(t,w,x,x,t)p(x,x,t)=p(t,w,x,x,t)p(w,x,x,t)p(w,x,x,t)p(x,x,t) =p(t|w,x,x,t)p(w|x,x,t) , 由于 t 关于 x 和 t 条件独立,因此 p(t|w,x,x,t) 可以简化为 p(t|w,x) ,而 w 与测试集中的点 x 无关,所以 p(w|x,x,t)=p(w|x,t) ,综合起来 p(t|x,x,t)=∫p(t|x,w)p(w|x,t)dw 。
参考文献
[1] Christopher M. Bishop, Pattern Recognition and Machine Learning, Springer, 2006.