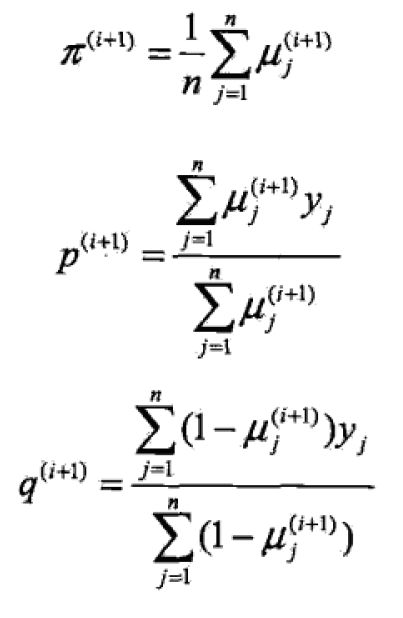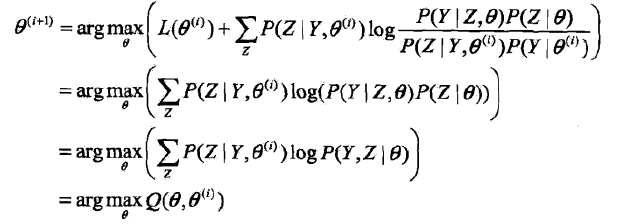EM算法

简介

ＥＭ算法是一种迭代算法，用于含有隐含变量（hidden variable）的概率模型参数的极大似然估计，或极大后验概率估计。EM算法的每次迭代由两部组成：E步，求期望（expectation）；M步，求极大值（maximization）。所以又称为期望极大算法（expectation maximization），简称ＥＭ算法

概率模型有时候同时含有观测变量和隐含变量，如果只含有观测变量，对于给定的数据，可直接根据极大似然估计或者贝叶斯估计模型参数。EM算法就是含有隐含变量的概率模型参数的极大似然估计。

极大似然估计

对于有 n 条样本的数据 X= { x1,x2,...,xn }, xi 是数据集中的第 i 条数据，模型参数是 Θ
似然函数是：
为了计算方便一般对上式去对数 logP(X|Θ)=logL(Θ|X)

上式取最大值时候的 Θ 就是模型参数的最优解

对 logL(Θ|X) 中的每个 Θk 求导 令等于0，求出所有的解，就是所求的 Θ

引例

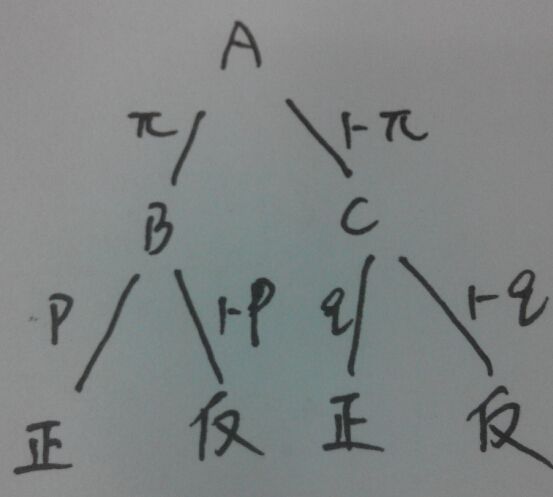
根据上图，能够很好的得出上面的等式。随机变量 y 是观测变量，就是我们上面输出的10次结果，表示输出结果0 或1 ，随机变量 z 是隐含变量，是我们无法观测到的，表示未观测到的掷硬币A的结果； Θ=(π,p,q) 是模型参数。

将观测数据表示为： Y=(Y1,Y2,...,Yn)T ，未观测数据表示为： Z=(Z1,Z2,...,Zn)T ，观测数据的似然函数为;
P(Y|Θ)=∑ZP(Z|Θ)P(Y|Z,Θ)
即：
求关于 Θ 的极大似然估计，即求

上面的问题没有解析解，只有通过迭代来实现。
ＥＭ算法首先选取参数的初值，记作 Θ(0)=(π(0),p(0),q(0)) ，然后通过下面的迭代计算参数的估计值，直到收敛。其中第i次迭代参数的估计值为 Θ(i)=(π(i),p(i),q(i))

E步：计算在模型参数 Θ(i)=(π(i),p(i),q(i)) 下观测数据 yj 来自掷硬币B的概率：

M步：计算模型参数的新估计值

对上面的问题：

一般地：用Y表示观测随机变量的数据，Z 表示隐含随机变量的数据。 Y和Z 在一起称为完全数据 (complete−data) ，观测数据 Y 又称为不完全数据。假设给定观测数据 Y ,和概率分布是 P(Y|θ) ，其中 |Theta 是需要估计的模型参数，那么不完全数据 Y 的似然函数是 P(Y|θ) ，对数似然函数 L(θ)=logP(Y|θ) ；假设 Y 和 Z 的联合概率分布是 P(Y,Z|θ) ，那么完全数据的对数似然函数是 logP(Y,Z|θ)

EM 算法通过迭代求 L(θ)=logP(Y,Z|θ) 的极大似然估计，每次迭代分为两步： E 步：求期望； M 步，求极大值。

EM 算法

输入：观测数据 Y ，隐含变量数据 Z ，联合分布 P(Y,Z|Θ) ，条件分布 P(Z|Y,θ)
输出：模型参数 θ
(1):选择参数的初始值 θ(0) ，开始迭代
(2): E 步：记 θ(i) 是第 i 次迭代参数 θ 的估计值，在第 i+1 次迭代的 E 步，计算

这里， P(Z|Y,θ(i)) 是在给定观测数据 Y 和当前的参数估计 θ(i) 下隐含变量 Z 的条件概率分布
(3): M 步：求使 Q(θ,θ(i)) 极大化的 θ ，确定第 i+1 次迭代的参数的估计值 θ(i+1)

EM 算法的导出

对含有隐含变量的概率模型，我们无法知道隐含变量，只有能利用到观测到的数据，我们极大化观测数据 Y 关于参数 θ 的对数似然函数，即极大化：
L(θ)=logP(Y|θ)=log∑zP(Y,Z|θ)
= log(∑zP(Y|Z,θ)P(Z|θ))
由于上式包含了隐含变量 Z ，直接简单的极大化上式是不可取的，所有只有通过迭代逐步近似极大化 L(θ)

设第 i 次迭代后的 θ 的估计值是 θ(i) ，我们希望新估计值 θ 能使 L(θ) 增加，即使 L(θ)>L(θ(i)) ，并逐步达到极大值。
L(θ)−L(θ(i))=log(∑zP(Y|Z,θ)P(Z|θ))−logP(Y|θ(i))
利用Jensen不等式
L(θ)−L(θ(i))=log(∑zP(Y|Z,θ)P(Z|θ))−logP(Y|θ(i))

=log(∑zP(Y|Z,θ(i))logP(Y|Z,θ)P(Z|θ)P(Y|Z,θ(i)))−logP(Y|θ(i))

>=∑zP(Z|Y,θ(i))logP(Y|Z,θ)P(Z|θ)P(Y|Z,θ(i))−logP(Y|θ(i))

=∑zP(Z|Y,θ(i))logP(Y|Z,θ)P(Z|θ)P(Z|Y,θ(i))P(Y|θ(i))

令 B(θ,θ(i))=L(θ(i))+∑zP(Z|Y,θ(i))logP(Y|Z,θ)P(Z|θ)P(Z|Y,θ(i))P(Y|θ(i))

则 ： L(θ)>=B(θ,θ(i))

即：函数 B(θ,θ(i)) 是 L(θ) 的一个下界

当 θ=θ(i) 时 L(θ(i))=B(θ(i),θ(i))

对任何可以使 B(θ,θ(i)) 增大的 θ ，也可以增大 L(θ) ，为了使 L(θ) 尽可能的增大，所有要选择 θ(i+1) 使 B(θ,θ(i)) 达到极大值，即

θ(i+1)=argmaxB(θ,θ(i))

现在求 θ(i+1) 的表达式

在上式的计算过程中， θ(i) 是已知的常数，我们求得是对于上式去的最大值时候的 θ ，可以在计算过程中消去无关常数项。

以上过程等价于 EM 算法的一次迭代，即求Q函数和及其最大化。 EM 算法就是在不断的求解下界的极大化逼近求解对数似然函数极大化大算法。

注意：
EM 算法不能保证所求的结果是全局最优解，这可能与选的初值有关系的。如下图的情况

应用

EM 算法可用于分类，回归，标注等问题，这个时候训练数据中的每个样本点由输入和输出对组成。
在用于分监督学习中，如分类问题时候，隐含变量就是类标签。

一个很好的例子：
http://www.r-bloggers.com/lang/chinese/1111

参考：《统计学习方法》李航