经典回溯——POJ 2488
对应POJ题目:点击打开链接
A Knight's Journey
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 30562 | Accepted: 10470 |
Description
 Background
Background
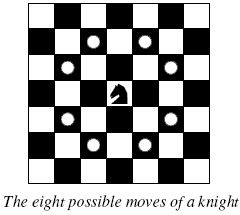
The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans?
Problem
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.
Input
The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .
Output
The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number.
If no such path exist, you should output impossible on a single line.
If no such path exist, you should output impossible on a single line.
Sample Input
3 1 1 2 3 4 3
Sample Output
Scenario #1: A1 Scenario #2: impossible Scenario #3: A1B3C1A2B4C2A3B1C3A4B2C4
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <map>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
const int MAXN=30;
int go[8][2] = {{-2, -1}, {-2, 1}, {-1, -2}, {-1, 2},{1, -2}, {1, 2}, {2, -1}, {2, 1}};
int G[MAXN][MAXN];
int res[MAXN][2];
int p,q,u;
char s[MAXN][3];
bool dfs(int i, int j)
{
if(i<1 || i>q || j<1 || j>p || G[i][j]) return 0;
res[u][0]=i+64;
res[u][1]=j;
if(++u==p*q)
{
for(i=0;i<u;++i) printf("%c%d", res[i][0],res[i][1]);
printf("\n");
return 1;
}
G[i][j]=1;
for( int d=0;d<8;++d)
{
int dx=i+go[d][0],dy=j+go[d][1];
if( dfs(dx,dy) ) return 1;
}
G[i][j]=0;
--u;
return 0;
}
int main()
{
//freopen("in.txt","r",stdin);
int T,w=0;
scanf("%d", &T);
while(T--)
{
printf("Scenario #%d:\n", ++w);
memset(res,0,sizeof(res));
scanf("%d%d", &p,&q);
int f=0;
for(int i=1; i<=q; i++){
for(int j=1; j<=p; j++){
memset(G,0,sizeof(G));
u=0;
if(dfs(i,j))
{
f=1;
break;
}
}
if(f) break;
}
if(!f) printf("impossible\n");
if(T) printf("\n");
}
return 0;
}