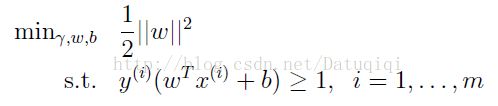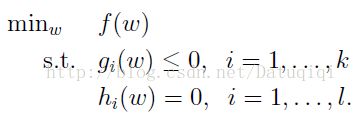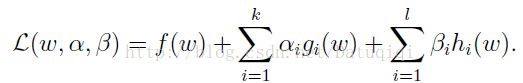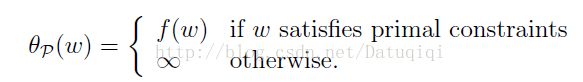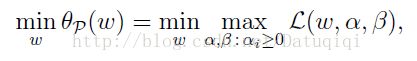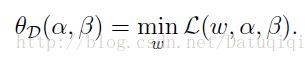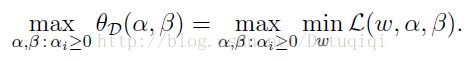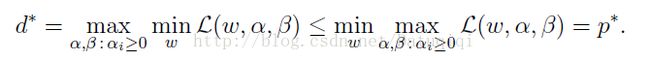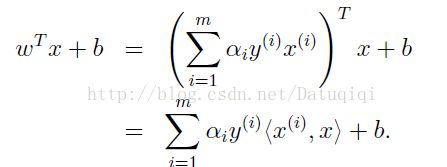Andrew NG机器学习课程笔记(七)
回想前面我们提到我们的目标是寻找一个超平面,使得离超平面比较近的点能有更大的间距。也就是我们不考虑所有的点都必须远离超平面,我们关心求得的超平面能够让所有点
中离它最近的点具有最大间距。形象的说,我们将上面的图看作是一张纸,我们要找一条折线,按照这条折线折叠后,离折线最近的点的间距比其他折线都要大。形式化表示为:
这里用||w||=1规约w,使得wTx+b是几何间隔。 到此,我们已经将模型定义出来了。如果求得了w和b,那么来一个特征x,我们就能够分类了,称为最优间隔分类器。接下的问题就是如何求解w和b的问题了。由于||w||=1不是凸函数,我们想先处理转化一下,考虑几何间隔和函数间隔的关系,γ=γ^/||w||,我们改写一下上面的式子:
这时候其实我们求的最大值仍然是几何间隔,只不过此时的w不受||w||=1的约束了。然而这个时候目标函数仍然不是凸函数,没法直接代入优化软件里计算。我们还要改写。前面说到同时扩大w和b对结果没有影响,但我们最后要求的仍然是w和b的确定值,不是他们的一组倍数值,因此,我们需要对γ^做一些限制,以保证我们解是唯一的。这里为了简便我们取γ^=1。这样的意义是将全局的函数间隔定义为1,也即是将离超平面最近的点的距离定义为1||w||。由于求
1||w||的最大值相当于求1/2||w||^2的最小值,因此改写后结果为:
这下好了,只有线性约束了,而且是个典型的二次规划问题(目标函数是自变量的二次函数)。代入优化软件可解。
到这里发现,这个讲义虽然没有像其他讲义一样先画好图,画好分类超平面,在图上标示出间隔那么直观,但每一步推导有理有据,依靠思路的流畅性来推导出目标函数和约束。 接下来介绍的是手工求解的方法了,一种更优的求解方法。
拉格朗日对偶
先抛开上面的二次规划问题,先来看看存在等式约束的极值问题求法,比如下面的最优化问题: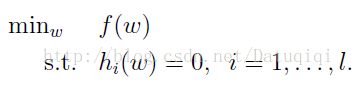
目标函数是f(w),下面是等式约束。通常解法是引入拉格朗日算子,这里使用β来表示算子,得到拉格朗日公式为
L是等式约束的个数。 然后分别对w和β求偏导,使得偏导数等于0,然后解出w和βi。至于为什么引入拉格朗日算子可以求出极值,原因是f(w)的dw变化方向受其他不等式的约束,dw的变化方向与f(w)的梯度垂直时才能获得极值,而且在极值处,f(w)的梯度与其他等式梯度的线性组合平行,因此他们之间存在线性关系。
然后我们探讨有不等式约束的极值问题求法,问题如下:
我们定义一般化的拉格朗日公式 :
这里的αi和βi都是拉格朗日算子。如果按这个公式求解,会出现问题,因为我们求解的是最小值,而这里的..i(..)≤0,我们可以将....调整成很大的正值,来使最后的函数结果是负无穷。因此我们需要排除这种情况,我们定义下面的函数:
这里的P代表primal。假设gi(w)>0或者hi(w)≠0,那么我们总是可以调整αi和βi来使得theta p(w)有最大值为正无穷。而只有
g和h满足约束时,theta p(w)为f(w)。这个函数的精妙之处在于αi≥0,而且求极大值。 因此我们可以写作
这样我们原来要求的min f(w)可以转换成求min theta p(w)了。
我们使用p*来表示min theta p(w)。如果直接求解,首先面对的是两个参数,而αi也是不等式约束,然后再在w上求最小值。这个过程不容易做,那么怎么办呢? 我们先考虑另外一个问题 :
D的意思是对偶,将问题转化为先求拉格朗日关于w的最小值,将α和β看作是固定值。之后再求最大值的话:
这个问题是原问题的对偶问题,相对于原问题只是更换了min和max的顺序,而一般更换顺序的结果是Max Min(X) <= Min Max(X)。然而在这里两者相等。用...来表示对偶问题如下:
下面解释在什么条件下两者会等价。假设f和g都是凸函数,h是仿射的(affine)。并且存在w使得对于所有的i,gi(w)<0。在这种假设下,一定存在w*,α*,β*使得w.是原问题的解,α*,β*是对偶问题的解。还有另外p*=d*=L(w*,α*,β*),w*,α*,β*满足库恩
-塔克条件(Karush-Kuhn-Tucker, KKT condition),该条件如下:
所以如果w*,α*,β*满足了库恩-塔克条件,那么他们就是原问题和对偶问题的解。让我们再次上述公式,这个条件称作是KKT dual complementarity条件。这个条件隐含了如果α*>0,那么gi(w*)=0。也就是说,gi(w*)=0时,w处于可行域的边界上,这时才是起作用的约束。而其他位于可行域内部(gi(w*)<0的)点都是不起作用的约束,其α*=0。这
个KKT双重补足条件会用来解释支持向量和SMO的收敛测试。
这部分内容思路比较凌乱,还需要先研究下《非线性规划》中的约束极值问题,再回头看看。KKT的总体思想是认为
极值会在可行域边界上取得,也就是不等式为0或等式约束里取得,而最优下降方向一般是这些等式的线性组合,其中每个元素要么是不等式为0的约束,要么是等式约束。对于在可行域边界内的点,对最优解不起作用,因此前面的系数为0。
我们通篇考虑问题的出发点是wTx+b,根据求解得到的αi,我们代入前式得到
也就是说,以前新来的要分类的样本首先根据w和b做一次线性运算,然后看求的结果是大于0还是小于0,来判断正例还是负例。现在有了αi,我们不需要求出w,只需将新来的样本和训练数据中的所有样本做内积和即可。