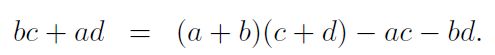算法课笔记系列（一）—— 分治算法

首先必须强调的是，我是个算法渣，多少年了~~还是渣/(ㄒoㄒ)/~~

这学期在上英文算法课，机缘巧合选了英文，觉得老师讲得还不错，所以没换到中文。想要通过这样总结一下加深算法理解，考试时也方便复习。

第一次课是对学习算法课需要的数学基础知识的复习，如集合以及集合的操作，函数，关系等，和一些数学证明方法的介绍，包括通过构造证明，通过对照证明（举反例，找矛盾），通过案例证明（可以理解为分情况讨论证明同一个结论对任一情况都成立），通过数学归纳法证明（包含最小反例法则，数学归纳的强法则）。

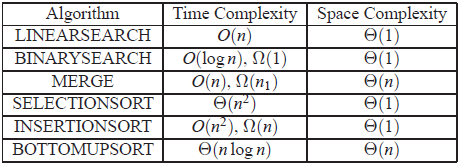
第二次课是接触算法必须的算法复杂度分析，包括时间和空间上的复杂度分析。通过列举了几个算法实际案例进行的分析，包括两种搜索方法（线性搜索，二分搜索），一个合并算法（将两个已经排好序的列表合并）和三种排序算法（选择排序，插入排序和合并排序）。

                                        

 第一个详细讲的算法是分治算法，该算法主要用于解决这样条件下的问题：

（1）      可以被分解成若干个相同的更小的子问题，即该问题具有最优子结构性质；分解到一定的程度就会很容易解决；

（2）      可以循环解决这些子问题；

（3）      最后可以合适的将子问题的解合并为该问题的解；

（4）      该问题分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题

实际问题就是逐一地解决这三个步骤：在将问题分解成子问题；在递归的最后一步，当问题变得足够小的时候，可以被直接解决了；以及将子问题的答案合并。

使用分治算法的经典例子如下：

（一）  乘法运算

（二）  Merge排序

（三）  求中位数

（四）  矩阵的乘法

先就乘法操作进行一下推导。

（一）  乘法操作

该算法是根据高斯的一个发现，将两个复数的乘法

                 

原本的四个乘法操作现在将其转化为三个，

                 

简单看来，认为减少的复杂度并不多。但是当应用到迭代中，会发现可以大大减小复杂度。

         对这个的证明可以将其从复数一般化到整型的乘法。假设x和y是两个n位的整数，为了方便假设n都是2的幂。由以上条件，我们可以将x和y转化为如下形式：

                  

这样一来，x和y的乘积可以表示为：

通过转化后的式子来计算xy，加法操作和这里的2的幂都是线性的复杂度，因为对2求幂就是一个左移的位操作。现在，乘法操作就变成了对四个n/2位的数进行乘法操作的迭代（子问题是原来大小的一半），然后在O(n)时间内将之前的结果进行整合。这样，使用master theorem来计算整个过程的复杂度的话就是

                  

计算得到算法的复杂度为O(n^2).

（备注：master theorem如下：

为了提升算法的运行效率，只用之前高斯提到的方法。原来的四个乘法操作可以转化为三个，

                

即

                                

这样的话，使用master theorem来计算整个过程的复杂度的话就是

                

，在每一次迭代中，常量从4变为3，计算出来复杂度为。

该问题的迭代过程可以通过一棵树来描述。

在子问题的每一次迭代中，问题的规模就减小一半。在次的迭代中，子问题的规模减小到1，迭代终止。因此，数的高度为。每一次迭代，问题的分支因子为3，也就是每次问题被分解为3个子问题，在第k层问题数目为3^k,每一个子问题的规模为在树的第k层需要的时间为

                     

在树的最高层，k=0，则复杂度为O(n)。在最底层，k=，计算出来为，可以写成，大约就是.

使用之前的思路，则这棵迭代数的分支因子为4，则计算，最后复杂度也需要这么多。

因此，在分治算法中，子问题的数目可以被解释为迭代树的分支因子（master theorem中的a），每一次问题规模的变化系数为b（减小一半就是1/2），最后将子问题的所有解合并起来的复杂度中n的幂指数即为d。

例如，二分查找中，在一个已经排好序的序列z[0,1,…,n-1]中找到数k，首先将k与z[2/n]进行比较，根据结果在决定是在前半部分继续比较还是后半部分继续比较。这样得到的迭代公式为，可以容易计算出该问题的复杂度为。

最后一部分讲了关于Sorting Network的画法，上课的时候听得比较模糊。下来整理一下之后，过程如下：

1）首先创建一个Bitonic Sorter

先说Bitonic sequence，中文翻译为双调序列，也就是单调递增和单调递减的的序列，也可以循环转换先单调递增再单调递减。

例如：

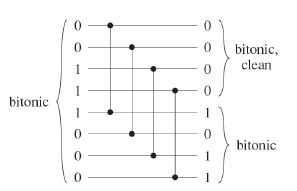
Half-cleaner是长度为1的比较网络，是第i个输入与第i+n/2个输入比较（假设n是偶数，i = 1,2,...n/2）

如下图：

          

这样得到的双调序列上半部分是更小的值，下半部分是更大的值。上下两部分都是双调的。

然后就可以画Bitonic Sorter的结构：

下面右图为n = 8时的Bitonic Sorter

              

2）第二步构造一个Merger

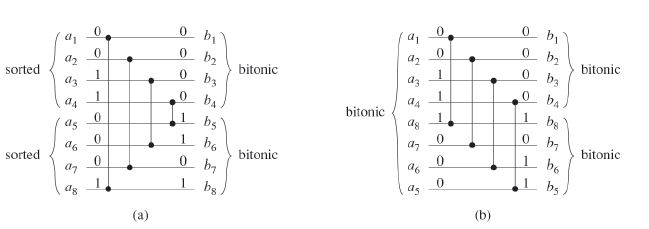
Merger与Half-cleaner是有区别的，Merger[n]是将两个单调的输入序列和转换成和..bn>, 而Half-CLeaner则是将转换成。其区别如下图：

             

于是构建的Merger如下：

                                

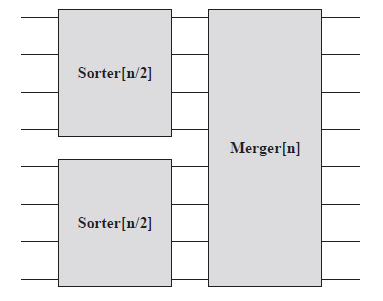
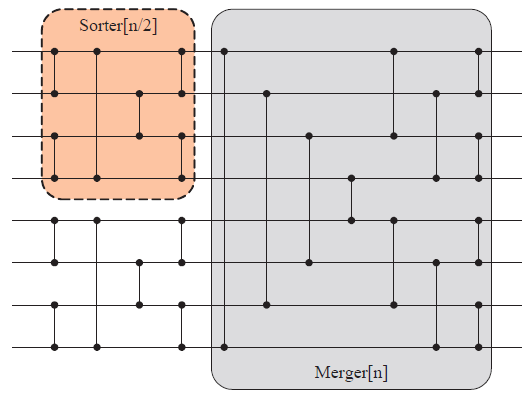
3）最后一步就是构造Sorter

                                

下面给出n=8和n=16时的sorting network：

n = 8:

                  

n = 16: