数据结构基础 之 最短路径 贪心算法
Dijkstra算法是解单源最短路径问题的贪心算法。其基本思想是,设置顶点集合点集合S并不断地做贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。初始时,S中仅含有源。设u是G的其一顶点。把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径,并用数组Distance记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶占,Distance就记录了从源到所有其它顶点之间最短路径长度。
例如下图中的有向图,应用Dijkstra算法计算从源顶点1到其它顶点最短路径的过程列表在下表中。
表格中默认选取的起始顶点为1顶点,所以本问题就转化为求解1顶点到2, 3, 4, 5这几个顶点的最短路径。首先初始条件列出1顶点到2, 3, 4, 5各个顶点的距离,这个距离直接在图的存储邻接矩阵中得到,选取距离最近的一个也就是2顶点加入集合S,下面要进行的是比较关键的一步,这个时候应该去获取3, 4, 5三个顶点到集合S的最短距离(从1顶点出发,可以经过S中的任意顶点):将1到2顶点的距离加上2到各个点的距离,然后用这个距离来同1到各个顶点的距离相比较,谁小就取谁,以此类推,然后每次取Distance[]最小的值进入集合S。
这样下去,Distance[]中存放的就是每个顶点到集合S的最短距离,比如当前的集合只有1, 2,按照规则顶点4应该入选进集合S,因为Distance[3]没有入选集合的顶点中对应的Distance[]最小的顶点。现在需要计算3和5到新集合S={1, 2, 4}的最短距离,这个时候就只需要将Distance[2]和Distance[4]中的值(现在这里面的值表示集合S={1, 2}到顶点3和5顶点的最短距离),但是现在集合中加入了顶点4,怎么计算?计算方法如下:
Distance[3] + 邻接矩阵中顶点4到顶点3的距离 < Distance[2] ?
Distance[3]:(顶点4到S={1, 2}的最短距离)
Distance[2]: (顶点3到S={1, 2}的最短距离)
如果这个小于成立,那么很明显新的集合到顶点3的最小距离应该是先从S={1, 2}到顶点4的最短距离,然后再从顶点4到顶点3。
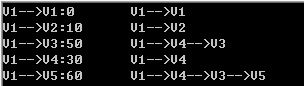
程序运行结果截图:
表格中默认选取的起始顶点为1顶点,所以本问题就转化为求解1顶点到2, 3, 4, 5这几个顶点的最短路径。首先初始条件列出1顶点到2, 3, 4, 5各个顶点的距离,这个距离直接在图的存储邻接矩阵中得到,选取距离最近的一个也就是2顶点加入集合S,下面要进行的是比较关键的一步,这个时候应该去获取3, 4, 5三个顶点到集合S的最短距离(从1顶点出发,可以经过S中的任意顶点):将1到2顶点的距离加上2到各个点的距离,然后用这个距离来同1到各个顶点的距离相比较,谁小就取谁,以此类推,然后每次取Distance[]最小的值进入集合S。
这样下去,Distance[]中存放的就是每个顶点到集合S的最短距离,比如当前的集合只有1, 2,按照规则顶点4应该入选进集合S,因为Distance[3]没有入选集合的顶点中对应的Distance[]最小的顶点。现在需要计算3和5到新集合S={1, 2, 4}的最短距离,这个时候就只需要将Distance[2]和Distance[4]中的值(现在这里面的值表示集合S={1, 2}到顶点3和5顶点的最短距离),但是现在集合中加入了顶点4,怎么计算?计算方法如下:
Distance[3] + 邻接矩阵中顶点4到顶点3的距离 < Distance[2] ?
Distance[3]:(顶点4到S={1, 2}的最短距离)
Distance[2]: (顶点3到S={1, 2}的最短距离)
如果这个小于成立,那么很明显新的集合到顶点3的最小距离应该是先从S={1, 2}到顶点4的最短距离,然后再从顶点4到顶点3。
由于每一次的比较都是在上一次集合的最优结果中计算的,所以新计算出来的顶点3到集合S={1, 2, 4}的最短距离也是全局最优的。
对应的C语言代码如下:
- #include <stdio.h>
- #define M 65535 //无穷大
- #define N 5 //顶点数
- //Dijkstra算法函数,求给定顶点到其余各点的最短路径
- //参数:邻接矩阵、出发点的下标、结果数组、路径前一点记录
- void Dijkstra(int Cost[][N], int v0, int Distance[], int prev[])
- {
- int s[N];
- int mindis,dis;
- int i, j, u;
- //初始化
- for(i=0; i<N; i++)
- {
- Distance[i] = Cost[v0][i];
- s[i] = 0;
- if(Distance[i] == M)
- prev[i] = -1;
- else
- prev[i] = v0;
- }
- Distance[v0] = 0;
- s[v0] = 1; //标记v0
- //在当前还未找到最短路径的顶点中,
- //寻找具有最短距离的顶点
- for(i=1; i < N; i++)
- {//每循环一次,求得一个最短路径
- mindis = M;
- u = v0;
- for (j=0; j < N; j++) //求离出发点最近的顶点
- if(s[j]==0 && Distance[j]<mindis)
- {
- mindis = Distance [j];
- u = j;
- } // if语句体结束,j循环结束
- s[u] = 1;
- for(j=0; j<N; j++) //修改递增路径序列(集合)
- if(s[j]==0 && Cost[u][j]<M)
- { //对还未求得最短路径的顶点
- //求出由最近的顶点 直达各顶点的距离
- dis = Distance[u] +Cost[u][j];
- // 如果新的路径更短,就替换掉原路径
- if(Distance[j] > dis)
- {
- Distance[j] = dis;
- prev[j] = u;
- }
- } // if 语句体结束,j循环结束
- } // i循环结束
- }
- // 输出最短路径
- // 参数:路径前一点记录、出发点的下标、到达点下标
- void PrintPrev(int prev[],int v0,int vn)
- {
- int tmp = vn;
- int i, j;
- //临时存路径
- int tmpprv[N];
- //初始化数组
- for(i=0; i < N; i++)
- tmpprv[i] = 0;
- //记录到达点下标
- tmpprv[0] = vn+1;
- //中间点用循环记录
- for(i =0, j=1; j < N ;j++)
- {
- if(prev[tmp]!=-1 && tmp!=0)
- {
- tmpprv[i] = prev[tmp]+1;
- tmp = prev[tmp];
- i++;
- }
- else break;
- }
- //输出路径,数组逆向输出
- for(i=N-1; i >= 0; i--)
- {
- if(tmpprv[i] != 0)
- { //排除0元素
- printf("V%d", tmpprv[i]);
- if(i) //不是最后一个输出符号
- printf("-->");
- }
- }
- printf("-->V%d", vn+1);
- }
- //主函数
- int main()
- {
- //给出有向网的顶点数组
- charchar *Vertex[N]={"V1", "V2", "V3", "V4", "V5"};
- //给出有向网的邻接矩阵
- int Cost[N][N]={
- {0, 10, M, 30, 100},
- {M, 0, 50, M, M},
- {M, M, 0, M, 10},
- {M, M, 20, 0, 60},
- {M, M, M, M, 0},
- };
- int Distance[N]; //存放求得的最短路径长度
- int prev[N]; //存放求得的最短路径
- int i;
- //调用Dijkstra算法函数,求顶点V1到其余各点的最短路径
- //参数:邻接矩阵、顶点数、出发点的下标、 结果数组
- Dijkstra(Cost, 0, Distance, prev);
- for(i=0; i < N; i++)
- {
- //输出最短路径长度
- printf("%s-->%s:%d\t", Vertex[0], Vertex[i], Distance[i]);
- //输出最短路径
- PrintPrev(prev, 0, i);
- printf("\n");
- }
- return 0;
- }