zoj zju 2994 Tiling a Grid With Dominoes 状压dp

Tiling a Grid With Dominoes Time Limit: 2 Seconds       Memory Limit: 65536 KB

We wish to tile a grid 4 units high and N units long with rectangles (dominoes) 2 units by one unit (in either orientation). For example, the figure shows the five different ways that a grid 4 units high and 2 units wide may be tiled.

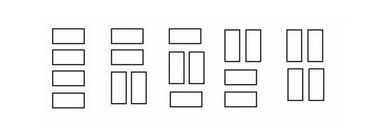
Write a program that takes as input the width, W, of the grid and outputs the number of different ways to tile a 4-by-W grid.

Input

The first line of input contains a single integer N, (1 <= N <= 1000) which is the number of datasets that follow.

Each dataset contains a single decimal integer, the width, W, of the grid for this problem instance.

Output

For each problem instance, there is one line of output: The problem instance number as a decimal integer (start counting at one), a single space and the number of tilings of a 4-by-W grid. The values of W will be chosen so the count will fit in a 32-bit integer.

Sample Input

3
2
3
7

Sample Output

1 5
2 11
3 781

题意，4*w的矩形放满1*2的矩形可以有多少种放法

从左往右状压dp。状态中的1表示横着放，且要占用该行下一列一格。0表示这个状态正好放满这列。

#include<stdio.h>
#include<string>
#include<iostream>
#include<map>
#include<string.h>
#include<algorithm>
using namespace std;

int dp[1200][20];// 1表示 需要下一行一个位子
int okling(int z)//判断z状态 是否 0 都是连续成对出现
{
	int flag=0; 
	int yiyi=3;
	for(int i=0;i<3;i++)
	{
		if(((z>>i)&yiyi)==0)
		{
			z|=(yiyi<<i);
		}
		else if(!(((z>>i)&yiyi)==3||(((z>>i)&yiyi)==1&&i!=2)))
			return 0;
	}
	return 1;
}
int ok(int z1,int z2)//左边列状态z1 右边列状态z2 可以匹配返回1
{
	for(int i=0;i<4;i++)
	{
		if(((z1>>i)&1)==1&&((z2>>i)&1)==1)
			return 0;
		else if(((z1>>i)&1)==1)
			z2=(z2|(1<<i));
	}

	if(okling(z2))
		return 1;
	else
		return 0;
}
int find(int wei,int m)//wei 这行 满足 wei+1行状态m的方法数。
{
	int ans=0;
	for(int i=0;i<16;i++)
	{
		if(ok(i,m))
			ans+=dp[wei][i];
	}
	return ans;
}
void init()
{
	memset(dp,0,sizeof dp);
	dp[0][0]=1;
	for(int i=1;i<=1000;i++)
	{
		for(int j=0;j<16;j++)//本行
		{
			dp[i][j]+=find(i-1,j);
		}
	}
}
int main()
{
	int t;  
	int cas=1; 
	int n;
	int op;
	init();
	scanf("%d",&t);

	while(t--)
	{
		scanf("%d",&n);
		printf("%d %d\n",cas++,dp[n][0]);
		
	}

	return 0;
}