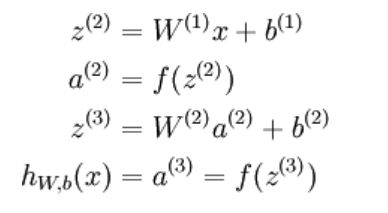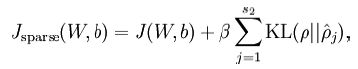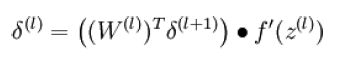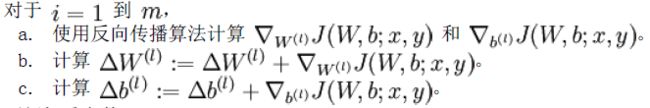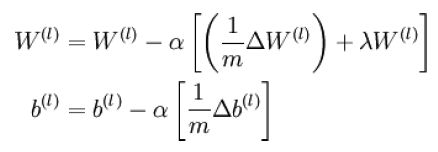UFLDL教程答案(1):Exercise:Sparse_Autoencoder

教程网址：http://deeplearning.stanford.edu/wiki/index.php/UFLDL%E6%95%99%E7%A8%8B

练习网址：http://deeplearning.stanford.edu/wiki/index.php/Exercise:Sparse_Autoencoder

自己实现代码的过程收获还是很多的，建议大家自己实现，我的答案给大家对比参考下。

1.重点公式回顾：

先列出教程中一些公式，方便与代码对应。

公式(1):

公式(2):

公式(3)：

公式(4):

公式(5):

公式(6):

公式(7):

公式(8):

公式(9):

公式(10):

公式(11):

 

2.反向传播推导过程中第l层第i个节点残差的推导过程：

教程中反向传播算法的推导中对于第3.步的推导(ng并没有在教程中给出推导，但是译者进行了推导)，我用了不同于译者的推导过程：

教程回顾及译者对第3步的推导：

我的推导过程：

等等，我找张纸。。。

当时每纸，一直没写上来，结果拖了好久，最近发现教程上这里的推导已经完全修改正确了，大家看教程就可以了。。。

3.进入正题：练习答案

Step 1: Generate training set

[x,y,z]=size(IMAGES);
imageNum=randi(z,1,numpatches);
patchX=randi(x-patchsize+1,1,numpatches);
patchY=randi(y-patchsize+1,1,numpatches);
for i=1:numpatches %1：10000
patch=IMAGES(patchX(i):patchX(i)+patchsize-1,patchY(i):patchY(i)+patchsize-1,imageNum(i));%取出一块patch
patches(:,i)=patch(:);%转为列向量放入patches
end

结果图如下：（运行时间用用tic，toc测得）

Step 2: Sparse autoencoder objective

m=size(data,2);
B1=repmat(b1,1,m);
B2=repmat(b2,1,m);
z2=W1*data+B1;
a2=sigmoid(z2);%(25,10000)
z3=W2*a2+B2;
a3=sigmoid(z3);%(64,10000)
%这几句：公式(1)%--------------
rho=sparsityParam;
rho_hat=sum(a2,2)/m;  %这句：公式(2)
KL=rho.*log(rho./rho_hat)+(1-rho).*log((1-rho)./(1-rho_hat));  %这句：公式(3)
cost=1/m*sum(sum((data-a3).^2)/2)+lambda/2*(sum(sum(W1.^2))+sum(sum(W2.^2)))+beta*sum(KL);   %这句：公式(4)公式(5)
%--------------
delta_sparsity=beta*(-rho./rho_hat+((1-rho)./(1-rho_hat)));  %公式(6)
delta3=(a3-data).*a3.*(1-a3);  %公式(7)
delta2=(W2'*delta3+repmat(delta_sparsity,1,m)).*a2.*(1-a2);   %公式(8)
W2grad=delta3*a2'/m+lambda*W2;  %后面这几句：公式(9)(10)(11)注意：矩阵相乘delta3*a2'和delata*data'隐含着公式(10)的m个样本求和
W1grad=delta2*data'/m+lambda*W1;
b2grad=sum(delta3,2)/m;
b1grad=sum(delta2,2)/m;

step2需step3完成后再进行验证。

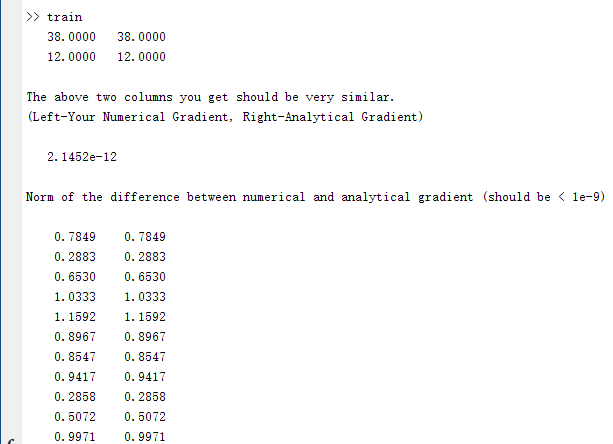
Step 3: Gradient checking

eps=0.0001;
thetaLen=length(theta);
thetaMat1=repmat(theta,1,thetaLen)+eye(thetaLen)*eps;
thetaMat2=repmat(theta,1,thetaLen)-eye(thetaLen)*eps;
for i=1:thetaLen
numgrad(i)=(J(thetaMat1(:,i))-J(thetaMat2(:,i)))/(2*eps);
end

用教程压缩包里提供的checkNumericalGradient.m文件测试step3，结果图如下，可以看到数值计算所得梯度与解析解所得梯度基本完全一致：

Step 4: Train the sparse autoencoder

压缩包中minFunc文件夹提供了L-BFGS方法代替简单的梯度下降，更好更快地奔向最小值。
step4 train.m文件没有什么需要写的地方，如果你觉得sparseAutoencoderCost.m文件写得没问题的话，直接运行train.m就可以得到结果了，大部分运行都花在时间train.m中STEP 3: Gradient Checking这里了，如果你已经验证好了你的梯度计算没有问题，那么之后可以把这部分注释掉。

train.m运行效果图如下：

可以看到数值计算的梯度和sparseAutoencoderCost计算的梯度完全一样，Function Val项为cost，越小越好，可以看到迭代400次，cost下降到了4.46213e-01（有时候到4.45......）。左为教程W1效果图，右为我的效果图，可以看到图像的边缘信息被提取了出来：