UFLDL教程答案(6):Exercise:Implement deep networks for digit classification
教程地址:http://deeplearning.stanford.edu/wiki/index.php/UFLDL%E6%95%99%E7%A8%8B
练习地址:http://deeplearning.stanford.edu/wiki/index.php/Exercise:_Implement_deep_networks_for_digit_classification
1.教程要点总结
1.预训练与微调
预训练(pre-training):在训练获得模型最初参数(利用自动编码器训练第一层,利用 logistic/softmax 回归训练第二层);
微调(fine-tune):我们可以进一步修正模型参数,进而降低训练误差。
微调具体来说是在现有参数的基础上采用梯度下降或者 L-BFGS 来降低已标注样本集 ![]() 上的训练误差。
上的训练误差。
微调的作用在于,已标注数据集可以用来修正权值 ![]() ,这样可以对隐藏单元所提取的特征
,这样可以对隐藏单元所提取的特征![]() 做进一步调整。
做进一步调整。
在什么时候应用微调?通常仅在有大量已标注训练数据的情况下使用。在这样的情况下,微调能显著提升分类器性能。然而,如果有大量未标注数据集(用于非监督特征学习/预训练),却只有相对较少的已标注训练集,微调的作用非常有限。
2.训练深度网络的困难
数据获取问题:我们需要依赖于有标签的数据才能进行训练。然而有标签的数据通常是稀缺的,在不充足的数据上进行训练将会导致过拟合。
局部极值问题:高度非凸的优化问题充斥着大量“坏”的局部极值。
梯度弥散问题:在使用随机初始化权重的深度网络上效果不好的技术原因是:随着网络的深度的增加,反向传播的梯度(从输出层到网络的最初几层)的幅度值会急剧地减小。整体的损失函数相对于最初几层的权重的导数非常小。当使用梯度下降法的时候,最初几层的权重变化非常缓慢,以至于它们不能够从样本中进行有效的学习。
3.逐层贪婪训练方法
逐层贪婪算法的主要思路是每次只训练网络中的一层,即我们首先训练一个只含一个隐藏层的网络,仅当这层网络训练结束之后才开始训练一个有两个隐藏层的网络,以此类推。在每一步中,我们把已经训练好的前![]() 层固定,然后增加第
层固定,然后增加第![]() 层(也就是将我们已经训练好的前
层(也就是将我们已经训练好的前![]() 的输出作为输入)。
的输出作为输入)。
每一层的训练可以是有监督的(例如,将每一步的分类误差作为目标函数),但更通常使用无监督方法(例如自动编码器,我们会在后边的章节中给出细节)。这些各层单独训练所得到的权重被用来初始化最终(或者说全部)的深度网络的权重,然后对整个网络进行“微调”(即把所有层放在一起来优化有标签训练集上的训练误差)。
数据获取:虽然获取有标签数据的代价是昂贵的,但获取大量的无标签数据是容易的。
更好的局部极值:当用无标签数据训练完网络后,相比于随机初始化而言,各层初始权重会位于参数空间中较好的位置上从而得到更好的局部极值。
4.栈式(多层)自编码神经网络
输入+自编码+自编码+softmax
栈式自编码神经网络的第一层会学习得到原始输入的一阶特征(比如图片里的边缘),第二层会学习得到二阶特征,该特征对应一阶特征里包含的一些模式(比如在构成轮廓或者角点时,什么样的边缘会共现)。栈式自编码神经网络的更高层还会学到更高阶的特征。
5.使用反向传播法进行微调(没有稀疏限制)
公式(1):对输出层(![]() 层),这里输出层是指第二层自编码层,
层),这里输出层是指第二层自编码层,![]()
(当使用softmax分类器时,softmax层满足:![]() ,其中
,其中![]() 为输入数据对应的类别标签, 为条件概率向量。)
为输入数据对应的类别标签, 为条件概率向量。)
公式(1)推导:见1.6
公式(2):对![]() ,
,![]()
公式(3):
6.公式(1)推导
![]() ,其中
,其中![]()
这个公式一开始没太明白如何得到的,经过与教程反向传导算法那部分及softmax回归那部分的反复对比,最终推导出了这个公式,对神经网络中的代价函数也有了更深的理解,下面来推导这个公式。
(a)先看看softmax回归那节的一个推导过程:
代价函数:
Softmax回归中将 ![]() 分类为类别
分类为类别![]() 的概率为:
的概率为:
梯度公式:
现在来推导这个梯度公式(为了避免混淆,把下标 j 改为了n):字丑勿怪
(b)我们想求残差![]() ,根据反向传导算法那节,需要先确定代价函数J,网络最后一层是softmax层,所以我们去softmax那节寻找代价函数:
,根据反向传导算法那节,需要先确定代价函数J,网络最后一层是softmax层,所以我们去softmax那节寻找代价函数:
此代价函数目的是使判断为真实类别的概率最大,由于极小化代价函数,所以前面加负号。对于残差的计算,是分别对每个样本求残差,所以上式前面的m个样本求和平均应该不要。
对比反向传导算法那节的代价函数:
极小化此代价函数使预测结果与真实值的差别尽可能小。
。。。好吧,想复制公式,打开了教程,发现新版的教程这里已经修改得这么好了,我之前在自编码器那个练习中提到的不太正确的残差推导也完全修改正确了,牛逼的译者。
残差计算:
同理:残差=代价函数对z求偏导,根据求导链式法则,代价函数先对a求导:(对于残差的计算,是分别对每个样本求残差,所以公式前面的m个样本求和平均不计算。)
然后再乘上a对z求导:(负号应该是代价函数中的那个负号,之前求导没有包含进来)
![]()
这样,就求得了最后一层自编码(就2层,就是第二层。。)的残差。之前层的残差按照反向传导算法那节公式计算即可。
2.进入正题
Step 1: Train the data on the first stacked autoencoder
使用了sparseAutoencoderCost.m
训练第一层自编码器,输入大小为inputSize(784),输出大小为hiddenSizeL1(200),输入数据为trainData(784*60000)
% Use minFunc to minimize the function
addpath minFunc/
options.Method = 'lbfgs';
options.maxIter = 400;
options.display = 'on';
[sae1OptTheta, sae1cost] = minFunc( @(p) sparseAutoencoderCost(p, ...
inputSize, hiddenSizeL1, ...
lambda, sparsityParam, ...
beta,trainData), ...
sae1Theta, options);
Step 2: Train the data on the second stacked autoencoder
使用了sparseAutoencoderCost.m
训练第二层自编码器,输入大小为hiddenSizeL1(200),输出大小为hiddenSizeL2(200),输入数据为sae1Features(200*60000,数据通过第一层自编码器的激活值)
[sae2OptTheta, sae2cost] = minFunc( @(p) sparseAutoencoderCost(p, ...
hiddenSizeL1, hiddenSizeL2, ...
lambda, sparsityParam, ...
beta,sae1Features), ...
sae2Theta, options);
Step 3: Train the softmax classifier on the L2 features
使用了softmaxCost.m
训练softmax,输入大小为hiddenSizeL2(200),输出大小为numClasses(10),输入数据为sae2Features(200*60000,第二层自编码的激活值) trainLabels(60000*1,样本类别,有监督学习),注意可以修改lambda的值,softmax那个练习用的lambda=1e-4,与训练自编码器时不同,其实我当时也忘了,用的lambda=3e-3,得出的结果并没有影响,训练还是挺耗时间的,我也没有试验lambda大小对结果的影响。
%lambda=1e-4;
[saeSoftmaxOptTheta, saeSoftmaxcost] = minFunc( @(p) softmaxCost(p, ...
numClasses, hiddenSizeL2, lambda, ...
sae2Features, trainLabels), ...
saeSoftmaxTheta, options);
Step 4: Implement fine-tuning
stackedAECost.m文件
计算微调时所需的梯度。softmax的参数按照之前softmax练习中的方法计算梯度;自编码器的参数梯度根据1.5中公式计算,由于自编码器预训练时已经考虑了稀疏性和正则化项,所有微调时自编码部分没有加入正则化项,教程中有提到:
Note: When adding the weight decay term to the cost, you should regularize only the softmax weights (do not regularize the weights that compute the hidden layer activations).
这段代码的实现纠结了好久,就是在这个z=cell{aeNumber,1}还是z=cell{aeNumber+1,1}上面,第二种会z{1},delta{1}这些都没使用,让我这种强迫症十分难受,但是用第一种会让代码和公式的标号对应得不好,代码读起来老觉得和公式不一样,最后还是用了第二种,代码标号和公式标号是一致的。
代码中有几个for循环其实就循环了一次,但是为了代码适用于任意层隐层,还是使用for循环。
aeNumber=numel(stack); %前向传播
m=size(data,2);
z = cell(aeNumber+1, 1);
a = cell(aeNumber+1, 1);
a{1}=data;
for i=2:aeNumber+1
z{i}=stack{i-1}.w*a{i-1}+repmat(stack{i-1}.b, 1, m);
a{i}=sigmoid(z{i});
end
%---------------------------------------------------------softmax参数的梯度
M=softmaxTheta*a{aeNumber+1};
M = bsxfun(@minus,M,max(M,[],1));
M=exp(M);
H = bsxfun(@rdivide,M,sum(M));
M=log(H);
M=M.*groundTruth;
cost=-1/m*sum(sum(M,1),2)+lambda/2*sum(sum(softmaxTheta.^2));
softmaxThetaGrad=-1/m*(groundTruth-H)*a{aeNumber+1}'+lambda*softmaxTheta;
%----------------------------------------------------------------自编码层参数梯度
delta=cell(aeNumber+1);
delta{aeNumber+1}=-(softmaxTheta'*(groundTruth-H)).*a{aeNumber+1}.*(1-a{aeNumber+1}); %公式(1)
for l=aeNumber:-1:2
delta{l}=(stack{l}.w'*delta{l+1}).*a{l}.*(1-a{l}); %公式(2)
end
for l=aeNumber:-1:1
stackgrad{l}.w=delta{l+1}*a{l}'/m; %公式(3)注意这里矩阵相乘隐含了m个样本求和
stackgrad{l}.b=sum(delta{l+1},2)/m;
end
stackedAEExercise.m
输入大小为inputSize(784),输入数据为trainData(784*60000)trainLabels(60000*1,样本类别,有监督学习)
[stackedAEOptTheta, cost3] = minFunc( @(p) stackedAECost(p, ...
inputSize, hiddenSizeL2, ...
numClasses, netconfig, ...
lambda, trainData, trainLabels), ...
stackedAETheta, options);
Step 5: Test the model
stackedAEPredict.m
aeNumber=numel(stack);
m=size(data,2);
z=cell(aeNumber+1,1);
a=cell(aeNumber+1,1);
a{1}=data;
for i=2:aeNumber+1
z{i}=stack{i-1}.w*a{i-1}+repmat(stack{i-1}.b,1,m);
a{i}=sigmoid(z{i});
end
theta_x=softmaxTheta * a{aeNumber+1};
[max_theta_x, pred]=max(theta_x);
结果和教程一致:
教程:对10类分类:about 87.7% before finetuning and 97.6% after finetuning
我:


![\begin{align}J(\theta) = - \frac{1}{m} \left[ \sum_{i=1}^{m} \sum_{j=1}^{k} 1\left\{y^{(i)} = j\right\} \log \frac{e^{\theta_j^T x^{(i)}}}{\sum_{l=1}^k e^{ \theta_l^T x^{(i)} }}\right]\end{align}](http://img.e-com-net.com/image/info5/d6dd48674ee1448490b4661b72aea9ec.png)
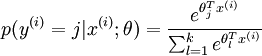
![\begin{align}\nabla_{\theta_j} J(\theta) = - \frac{1}{m} \sum_{i=1}^{m}{ \left[ x^{(i)} \left( 1\{ y^{(i)} = j\} - p(y^{(i)} = j | x^{(i)}; \theta) \right) \right] }\end{align}](http://img.e-com-net.com/image/info5/4cc7343b1f8549a78356edb907085047.png)


