Fisher vector学习笔记

1，背景

     现有的模式分类方法主要分为两类，一类是生成式方法，比如GMM，这类方法主要反映同类数据之间的相似度；一类是判别式方法，比如SVM，主要是反映异类数据之间的差异。fisher kernel是想要结合二者的优势（1，生成式方法可以处理长度不一的输入数据，2，判别式方法不能处理长度不一的数据但是分类效果较好。），将生成式模型用于判别式分类器中。

     关于处理长度不一的数据，举例说明如下：
     我们要对一个图片集 I=X1,X2... 中的图片做分类，考虑生成式的方法，GMM，是对每一幅图片 Xi=x1,...xT 的特征 xi 建模(每个 xi 是D维特征向量)，T代表一幅图片中提取的特征点个数，所以T的大小变化，不影响GMM建模。但是判别式分类器如SVM中是要计算样本X之间的距离，如果每个X的特征点个数T不一样，那么他们的维度也就不一样，无法计算他们之间的距离。

     论文《Exploiting generative models in discriminative classifiers》中对fisher kernel进行了理论上的一系列推导和阐述。论文《Fisher Kernel on Visual Vocabularies for Image Categorization》中fisher kernel被应用于图像分类，本文主要参考这篇。论文《Improving the Fisher Kernel for Large-Scale Image Classification》中对fisher vector做改进。

     fisher kernel被应用于图像分类的主要思路是，用生成式模型(GMM)对样本输入进行建模，进而得到样本的一种表示(fisher vector)，再将这种表示(fisher vector)输入判别式分类器(SVM)得到图像分类结果。fisher vector是fisher kernel中对样本特征的一种表示，它把一幅图片表示成一个向量。
     本文主要关注fisher vector。

2，fisher kernel

     核方法可以定义一种基于核函数的判别式分类器，可表示如下：

Snew=sign(∑iSiλiK(Xi,Xnew))

      Xi,Si 是训练集中样本i的值和它的label值，label值只能取+1和-1，也就是分成两类， λi 是样本i在训练集中所占的权重；
      Xnew，Snew 是一个新来的样本值和分类器预测出得它的label值；
     这里的 K(Xi,Xnew) 是一个核函数，度量新样本 Xnew 和训练集样本 Xi 之间的相似度。

     所以需要确定 λ 和核函数 K(Xi,Xj) 就可以确定一种基于核的分类方法。其中 λ 可以通过做一些优化得到，而在fisher kernel中，就是利用fisher信息矩阵得到一个核函数来度量样本相似度。

     对于一个核函数，有如下的形式：

K(Xi,Xj)=ϕTXiϕXj.

     这里是一个内积的形式，我们将一幅图片的特征们X映射到一个新的特征向量，也就是 ϕX ，那么这个内积就是这两个新特征向量 ϕXi,ϕXj 的欧式距离，很直观地反映了样本i,j之间的相似度。

     这个 ϕX 就是fisher kernel中的样本表示方法，它就是fisher vector，它由fisher score归一化得到， Fλ 是fisher信息矩阵：

ϕX=F−12λUx.

     定义fisher score:
     

Ux=∇λlogp(X|λ).

     X服从分布p，p的参数是 λ ，在fisher kernel中，p是一个GMM， X=x1,...xT 是一幅图片的特征集合（可以用sift特征）， λ ={ wi,μi,∑i,i=1...N }，它是GMM的模型参数， wi 是GMM中第i个component的权重， μi,∑i 是均值和协方差，由高斯模型的原理可知这两个都是向量，且和特征向量 xt 的维度一致，都是D维（如果 xt 是一个sift特征向量，那么它们就是128维）。
     这个log似然函数对 λ 的梯度，描述了参数 λ 在p生成特征点集合X的过程中如何作用，所以这个fisher score中也包含了GMM生成X的过程中的一些结构化的信息。

      F−12λ 是用来对 Ux 做归一化的，所以 Fλ=UXUTX ，这里来证明一下这个归一化，记 V=UX :

[(VVT)−12V]T[(VVT)−12V]=VT[(VVT)−12]T(VVT)−12V=VT(VVT)−1VVTV=1

     所以核函数就有了如下分解形式：

K(Xi,Xj)=UTXiF−1λUXj

     这里要求 F−1λ 是半正定的，所以给F求期望： Fλ=Ex(UXUTX).

     至此，我们就能对一幅图片的特征点集合计算出fisher vector了。

3，计算fisher vector

     首先定义：

L(X|λ)=logp(X|λ)=∑t=1Tlogp(xt|λ).

     由于一幅图片中的特征点是相互独立的，所以：

p(xt|λ)=∑i=1Nwipi(xt|λ).

      pi 是GMM中第i个component的pdf， wi 是其权值， ∑Ni=1wi=1.
component pi 的pdf是多元高斯函数，如下：

     再定义特征 xt 由第i个Gaussian component生成的概率：

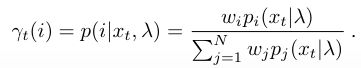
     首先对参数求偏导可得到:

UX=[∂L(X|λ)∂wi,∂L(X|λ)∂μdi,∂L(X|λ)σdi]T,i=1...N.

     其中

     注意这里i是指第i个component，d是指特征 xt 的第d维，偏导是对每个component，对特征每个维度都要计算，所以此时 UX 的维度是(2D+1)*N，D是 xt 维度，N是component个数。又由于 wi 有约束 ∑iwi=1 ，所以会少一个自由变量，所以 UX 最终的维度是(2D+1)*N-1.

     求得 UX 后，就可以求 Fλ ，设F中对角线上的元素可以表示为 fwi,fμdi,fσdi , 通过简单的求期望运算就可以得到它们的值：

     这里算得的矩阵F两个维度都是(2D+1)*N-1.

     所以fisher vector

ϕX=[Xw,d,i,Xμ,d,i,Xσ,d,i]=[f−1/2wi∂L(X|λ)∂wi,f−1/2μdi∂L(X|λ)∂μdi,f−1/2σdi∂L(X|λ)∂σdi].

     维度和 UX 一样，也是(2D+1)*N-1.

4，总结

     fisher vector的结果是对原图像特征升维了（从D到(2D+1)*N-1），它从图像的一种特征向量中挖掘了出更丰富的信息，最终对 ϕX 我们可以算得对均值和协方差的梯度:

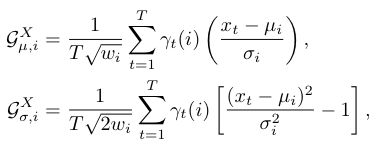
     可以看到，D维向量 xt 中的每一个值，都与均值和方差做运算，并加上权重，fisher vector中包含了原特征向量每一维的值，并且包含了生成式建模过程的结构性信息，对图片的表达更加细致。