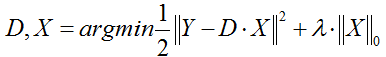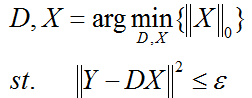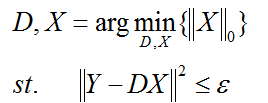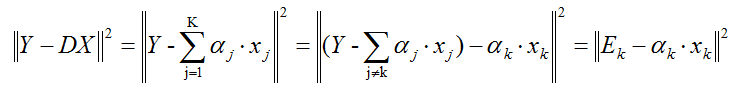机器学习(十三)k-svd字典学习
k-svd字典学习
原文地址:http://blog.csdn.net/hjimce/article/details/50810129
作者:hjimce
一、字典学习
字典学习也可简单称之为稀疏编码,字典学习偏向于学习字典D。从矩阵分解角度,看字典学习过程:给定样本数据集Y,Y的每一列表示一个样本;字典学习的目标是把Y矩阵分解成D、X矩阵:
同时满足约束条件:X尽可能稀疏,同时D的每一列是一个归一化向量。
D称之为字典,D的每一列称之为原子;X称之为编码矢量、特征、系数矩阵;字典学习可以有三种目标函数形式
(1)第一种形式:
这种形式因为L0难以求解,所以很多时候用L1正则项替代近似。
(2)第二种形式:
ε是重构误差所允许的最大值。
(3)第三种形式:
L是一个常数,稀疏度约束参数,上面三种形式相互等价。
因为目标函数中存在两个未知变量D、X,K-svd是字典学习的一种经典算法,其求解方法跟lasso差不多,固定其中一个,然后更新另外一个变量,交替迭代更新。
如果D的列数少于Y的行数,就相当于欠完备字典,类似于PCA降维;如果D的列数大于Y的行数,称之为超完备字典;如果刚好等于,那么就称之为完备字典。
二、k-svd字典学习算法概述
给定训练数据Y,Y的每一列表示一个样本,我们的目标是求解字典D的每一列(原子)。K-svd算法,个人感觉跟k-means差不多,是k-means的一种扩展,字典D的每一列就相当于k-means的聚类中心。其实球面k-means也是一种特殊的稀疏编码(具体可参考文献《Learning Feature Representations with K-means》),只不过k-means的编码矩阵X是一个高度稀疏的矩阵,X的每一列就只有一个非零的元素,对应于该样本所归属的聚类中心;而稀疏编码X的每一列允许有几个非零元素。
1、随机初始化字典D(类似k-means一样初始化)
从样本集Y中随机挑选k个样本,作为D的原子;并且初始化编码矩阵X为0矩阵。
2、固定字典,求取每个样本的稀疏编码
编码过程采用如下公式:
ε是重构误差所允许的最大值。
假设我们的单个样本是向量y,为了简单起见我们就假设原子只有这4个,也就是字典D=[α1、α2、α3、α4],且D是已经知道的;我们的目标是计算y的编码x,使得x尽量的稀疏。
(1)首先从α1、α2、α3、α4中找出与向量y最近的那个向量,也就是分别计算点乘:
α1*y、α2*y、α3*y、α4*y
然后求取最大值对应的原子α。
(2)假设α2*y最大,那么我们就用α2,作为我们的第一个原子,然后我们的初次编码向量就为:
x1=(0,b,0,0)
b是一个未知参数。
(3)求解系数b:
y-b*α2=0
方程只有一个未知参数b,是一个高度超静定方程,求解最小二乘问题。
(4)然后我们用x1与α2相乘重构出数据,然后计算残差向量:
y’=y-b*α2
如果残差向量y’满足重构误差阈值范围ε,那么就结束,否则就进入下一步;
(5)计算剩余的字典α1、α3、α4与残差向量y’的最近的向量,也就是计算
α1*y’、α3*y’、α4*y’
然后求取最大值对应的向量α,假设α3*y’为最大值,那么就令新的编码向量为:
x2=(0,b,c,0)
b、c是未知参数。
(6)求解系数b、c,于是我们可以列出方程:
y-b*α2-c*α3=0
方程中有两个未知参数b、c,我们可以进行求解最小二乘方程,求得b、c。
(7)更新残差向量y’:
y’=y-b*α2-c*α3
如果y’的模长满足阈值范围,那么就结束,否则就继续循环,就这样一直循环下去。
3、逐列更新字典、并更新对应的非零编码
通过上面那一步,我们已经知道样本的编码。接着我们的目标是更新字典、同时还要更新编码。K-svd采用逐列更新的方法更新字典,就是当更新第k列原子的时候,其它的原子固定不变。假设我们当前要更新第k个原子αk,令编码矩阵X对应的第k行为xk,则目标函数为:
上面的方程,我们需要注意的是xk不是把X一整行都拿出来更新(因为xk中有的是零、有的是非零元素,如果全部抽取出来,那么后面计算的时候xk就不再保持以前的稀疏性了),所以我们只能抽取出非零的元素形成新的非零向量,然后Ek只保留xk对应的非零元素项。
上面的方程,我们可能可以通过求解最小二乘的方法,求解αk,不过这样有存在一个问题,我们求解的αk不是一个单位向量,因此我们需要采用svd分解,才能得到单位向量αk。进过svd分解后,我们以最大奇异值所对应的正交单位向量,作为新的αk,同时我们还需要把系数编码xk中的非零元素也给更新了(根据svd分解)。
然后算法就在1和2之间一直迭代更新,直到收敛。
#更新字典第k列,<span style="font-family: Arial, Helvetica, sans-serif;">phi为字典,y为样本集、sparse为上面稀疏编码矩阵X</span>
def dict_update(phi, matrix_y, matrix_sparse, k):
indexes = np.where(matrix_sparse[k, :] != 0)[0]#取出稀疏编码中,第k行不为0的列的索引
phi_temp = phi
sparse_temp = matrix_sparse
if len(indexes) > 0:
phi_temp[:, k][:] = 0#把即将更新的字典的第k列先给设置为0
matrix_e_k = matrix_y[:, indexes] - phi_temp.dot(sparse_temp[:, indexes])#取出样本数据中,字典第k列有贡献的值,并求Ek
u, s, v = svds(np.atleast_2d(matrix_e_k), 1)
phi_temp[:, k] = u[:, 0]
sparse_temp[k, indexes] = np.asarray(v)[0] * s[0]
return phi_temp, sparse_temp
参考文献:
1、《Learning Feature Representations with K-means》
2、Restauration parcimonieuse d'unsignal multidimensionnel :algorithme K-SVD
**********作者:hjimce 联系qq:1393852684 原创文章,转载请保留原文地址、作者信息******************