SparkML之聚类(一)Kmeans聚类

------------------------------目录--------------------------------------------------

Kmeans理论

Matlab实现

Spark源码分析

Spark源码

Spark实验

------------------------------------------------------------------------------------

Kmeans聚类理论可以访问http://cs229.stanford.edu/notes/cs229-notes7a.pdf

可以总结下面三点

1、初始化K个聚类中心点

2、计算每个点到K个聚类中心的距离

3、根据距离，寻找更好的K个聚类中心点

问题1：怎么确定这K个了？随机选择还是有算法确定

解答：我们可以随机选择这K个点，也可以用算法确定这K个点，一般用K-mean++算法进行对K个点的选择

详细的K-mean++算法访问（https://en.wikipedia.org/wiki/K-means%2B%2B和http://theory.stanford.edu/~sergei/papers/vldb12-kmpar.pdf.），具体流程如下：

1、从输入的数据集中随机选择一个点作为第一个聚类中心C1

2、计算每个数据点到C1的距离,保存在D（x）中

3、选择D（x）中最大距离的那个数据点作为第二个聚类中心C2

4、计算每个数据点到C1、C2的距离，那个聚类中心里这个数据点近，那么这个数据点就数据这个聚类中心

那么此时，所有的数据点分为2类，一类是依附于C1，另一类是依附于C2

问题2：当K大于2怎么办？那么是不是我们依附于C1、C2的距离都放在一个D(X),在按照那个距离最大，选哪个

解答：這是可以的！算法嘛，总是希望做的和别人有更优之处，要想更优，那么就得考虑更多，下面就是考虑更多的

结果

5、计算每个数据点到最近聚类中心的距离（比如4中，计算C1类的点到C1的距离，C2类的点到C2的距离），之后

对所有的距离进行求和得到Sum

6、取(0,sum)之间的一个随机值记为temp，让temp = temp -  (i = 1,2,...),当temp <0 的那一刻，就取这个（i）

点，那么这个i点就是下一个聚类中心

7、就這样一直寻找到第K个点

现在结合matlab编写函数进行讲解

数据和代码，百度云链接;链接：http://pan.baidu.com/s/1mh9ldnM 密码：dcz4

%导入数据
filename = 'C:\Users\andrew\Desktop\kmeans\IrisData.txt';
delimiter = '\t';
startRow = 2;
formatSpec = '%f%f%f%f%s%[^\n\r]';
fileID = fopen(filename,'r');
dataArray = textscan(fileID, formatSpec, 'Delimiter', delimiter, 'HeaderLines' ,startRow-1, 'ReturnOnError', false);
VarName1 = dataArray{:, 1};
Sepalwidth = dataArray{:, 2};%萼片宽
Petallength = dataArray{:, 3};%花瓣长度
Petalwidth = dataArray{:, 4};%花瓣宽度
Species = dataArray{:, 5};%种类

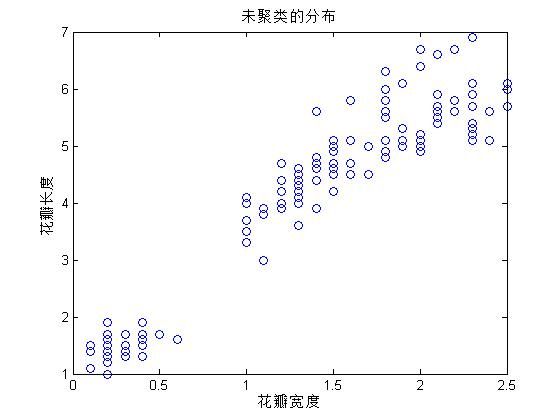
%查看样本的分布情况
figure(1)
plot(Petalwidth,Petallength,'o')
xlabel('花瓣宽度')
ylabel('花瓣长度')
title('未聚类的分布')

%为了更加直观，把不同的种类用不同的符号标记出来
%1到50的种类为：   I. setosa
%51到100的种类为： I. versicolor
%101到150的种类为：I. virginica
figure(2)
hold on
plot(Petalwidth(1:50),Petallength(1:50),'rs','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g','MarkerSize',10)
plot(Petalwidth(51:100),Petallength(51:100),'mo','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor',[.49 1 .63],'MarkerSize',10)
plot(Petalwidth(101:end),Petallength(101:end),'rh','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','r','MarkerSize',10)
xlabel('花瓣宽度')
ylabel('花瓣长度')
title('实际类别分布情况')
hold off


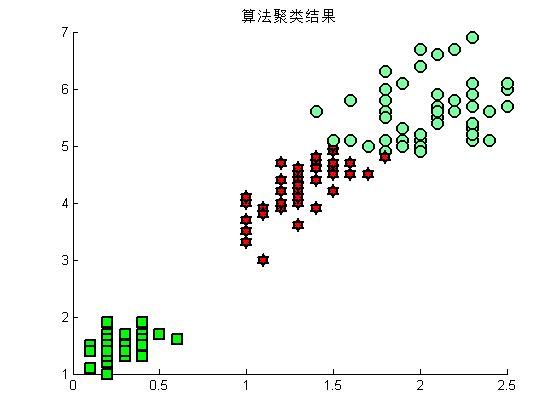
%调用 自己编写的kmeans，看看效果
X = [Petalwidth,Petallength];
[cid,nr,centers] = mykmeans(X,3);
figure(3)
hold on
for i = 1:length(Petalwidth)
    if cid(i) ==1
        plot(Petalwidth(i),Petallength(i),'rs','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','g','MarkerSize',10)
    end
    if cid(i) ==2
        plot(Petalwidth(i),Petallength(i),'mo','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor',[.49 1 .63],'MarkerSize',10)
    end
    if cid(i) ==3
        plot(Petalwidth(i),Petallength(i),'rh','LineWidth',2,'MarkerEdgeColor','k','MarkerFaceColor','r','MarkerSize',10)
    end
end
title('算法聚类结果')
hold off
        
%centers =
%
%    2.0478    5.6261
%    0.2460    1.4620
%    1.3593    4.2926

function [cid,nr,centers] = mykmeans(X,k)
%参数说明
%   X：数据集（n*m）
%   k：输入的聚类中心个数
%   cid:每一个数据输入那一类
%    nr:每个数据的个数
%   centers:每个类的聚合中心（集合）

%%寻找初始的k个聚类中心


[n,m]=size(X);
cid = zeros(1,n);
nr = zeros(1,k);

%从输入的数据集中随机找出k个聚类中心
temp = randperm(n);
a = temp(1:k);
nc= X(a',:);

%开始对k个聚类中心进行优化
maxIter = 100;
iter = 1;
while iter < maxIter
    for i = 1:n
         dist = sum((repmat(X(i,:),k,1)-nc).^2,2); 
         [~,ind] = min(dist); 
          cid(i) = ind;
    end
    for i = 1:k
        ind = find(cid==i); 
        nc(i,:) = mean(X(ind,:)); 
        nr(i) = length(ind); 
    end
    iter = iter + 1;
end 
tempMaxiter = 2;
tempIter = 1;
tempMove = 1;
while tempIter < tempMaxiter && tempMove ~= 0 
    tempMove = 0; 
    for i = 1:n
        dist = sum((repmat(X(i,:),k,1)-nc).^2,2); 
        r = cid(i);
        dadj = nr./(nr+1).*dist';
        [~,ind] = min(dadj);
         if ind ~= r 
                   cid(i) = ind;
                   ic = find(cid==ind);
                   nc(ind,:) = mean(X(ic,:)); 
                   tempMove = 1; 
         end
    end
    tempIter = tempIter+1;
end
centers = nc;
end

SparkML源码分析

Spark对于Kmeans算法程序一共有：KMeans类和KMeans同名对象。

VectorWithNorm类（自行设定norm，为fastSquaredDistance函数服务）

KMeansModel类和KMeansModel同名对象

作用：

KMeans类：

设定训练的参数（聚类中心数目：k,最大迭代次数： maxIterations并行数：runs（默认是1），

初始化算法：initializationMode，种子：seed，收敛值：Epsilon等）

训练模型（run）:初始化中心（随机方法和K-mean++算法），聚类中心点计算（runAlogorithm）

初始化并行度（initKMeansParallel）

KMeans同名对象

对不同输入格式，书写train方法

找里各个聚类中心最近的点（findClosest）和计算距离（pointCost）

快速距离计算（fastSquaredDistance）

KMeansModel类

计算每个样本到最近聚类中心的距离（computeCost）

保存模型（save）

预测（predict）

KMeansModel同名对象

导入模型（load）

当前模型的版本号处理（object SaveLoadV1_0）

spark源码：

Kmeans类

@Since("0.8.0")
class KMeans private (
                       private var k: Int,
                       private var maxIterations: Int,
                       private var runs: Int,
                       private var initializationMode: String,
                       private var initializationSteps: Int,
                       private var epsilon: Double,
                       private var seed: Long) extends Serializable with Logging {

  /**  * Constructs a KMeans instance with default parameters: {k: 2, maxIterations: 20, runs: 1,  * initializationMode: "k-means||", initializationSteps: 5, epsilon: 1e-4, seed: random}.  */  //构造函数：
  //默认情况下：分2类，20次迭代，1个并行，输出化模型选择KMeans.K_MEANS_PARALLEL，初始steps为5
  //epsilon = 0.0001，
  @Since("0.8.0")
  def this() = this(2, 20, 1, KMeans.K_MEANS_PARALLEL, 5, 1e-4, Utils.random.nextLong())

  /**  * Number of clusters to create (k).  */  @Since("1.4.0")
  def getK: Int = k

  /**  * Set the number of clusters to create (k). Default: 2.  */  @Since("0.8.0")
  def setK(k: Int): this.type = {
    this.k = k
    this  }

  /**  * Maximum number of iterations allowed.  */  @Since("1.4.0")
  def getMaxIterations: Int = maxIterations

  /**  * Set maximum number of iterations allowed. Default: 20.  */  @Since("0.8.0")
  def setMaxIterations(maxIterations: Int): this.type = {
    this.maxIterations = maxIterations
    this  }

  /**  * The initialization algorithm. This can be either "random" or "k-means||".  */  @Since("1.4.0")
  def getInitializationMode: String = initializationMode

  /**  * Set the initialization algorithm. This can be either "random" to choose random points as  * initial cluster centers, or "k-means||" to use a parallel variant of k-means++  * (Bahmani et al., Scalable K-Means++, VLDB 2012). Default: k-means||.  */  @Since("0.8.0")
  def setInitializationMode(initializationMode: String): this.type = {
    KMeans.validateInitMode(initializationMode)
    this.initializationMode = initializationMode
    this  }

  /**  * :: Experimental ::  * Number of runs of the algorithm to execute in parallel.  */  @Since("1.4.0")
  @deprecated("Support for runs is deprecated. This param will have no effect in 2.0.0.", "1.6.0")
  def getRuns: Int = runs

  /**  * :: Experimental ::  * Set the number of runs of the algorithm to execute in parallel. We initialize the algorithm  * this many times with random starting conditions (configured by the initialization mode), then  * return the best clustering found over any run. Default: 1.  */  @Since("0.8.0")
  @deprecated("Support for runs is deprecated. This param will have no effect in 2.0.0.", "1.6.0")
  def setRuns(runs: Int): this.type = {
    internalSetRuns(runs)
  }

  // Internal version of setRuns for Python API, this should be removed at the same time as setRuns
  // this is done to avoid deprecation warnings in our build.
  private[mllib] def internalSetRuns(runs: Int): this.type = {
    if (runs <= 0) {
      throw new IllegalArgumentException("Number of runs must be positive")
    }
    if (runs != 1) {
      logWarning("Setting number of runs is deprecated and will have no effect in 2.0.0")
    }
    this.runs = runs
    this  }

  /**  * Number of steps for the k-means|| initialization mode  */  @Since("1.4.0")
  def getInitializationSteps: Int = initializationSteps

  /**  * Set the number of steps for the k-means|| initialization mode. This is an advanced  * setting -- the default of 5 is almost always enough. Default: 5.  */  @Since("0.8.0")
  def setInitializationSteps(initializationSteps: Int): this.type = {
    if (initializationSteps <= 0) {
      throw new IllegalArgumentException("Number of initialization steps must be positive")
    }
    this.initializationSteps = initializationSteps
    this  }

  /**  * The distance threshold within which we've consider centers to have converged.  */  @Since("1.4.0")
  def getEpsilon: Double = epsilon

  /**  * Set the distance threshold within which we've consider centers to have converged.  * If all centers move less than this Euclidean distance, we stop iterating one run.  */  @Since("0.8.0")
  def setEpsilon(epsilon: Double): this.type = {
    this.epsilon = epsilon
    this  }

  /**  * The random seed for cluster initialization.  */  @Since("1.4.0")
  def getSeed: Long = seed

  /**  * Set the random seed for cluster initialization.  */  @Since("1.4.0")
  def setSeed(seed: Long): this.type = {
    this.seed = seed
    this  }

  // Initial cluster centers can be provided as a KMeansModel object rather than using the
  // random or k-means|| initializationMode
  private var initialModel: Option[KMeansModel] = None

  /**  * Set the initial starting point, bypassing the random initialization or k-means||  * The condition model.k == this.k must be met, failure results  * in an IllegalArgumentException.  */  @Since("1.4.0")
  def setInitialModel(model: KMeansModel): this.type = {
    require(model.k == k, "mismatched cluster count")
    initialModel = Some(model)
    this  }

  /**  * Train a K-means model on the given set of points; `data` should be cached for high  * performance, because this is an iterative algorithm.  */  @Since("0.8.0")
  //训练模型的run方法
  //官方提示说，因为迭代最好选择将数据进行缓存
  def run(data: RDD[Vector]): KMeansModel = {

    if (data.getStorageLevel == StorageLevel.NONE) {
      logWarning("The input data is not directly cached, which may hurt performance if its"
        + " parent RDDs are also uncached.")
    }

    // Compute squared norms and cache them.
    //计算2范数，并且缓存
    val norms = data.map(Vectors.norm(_, 2.0))
    norms.persist()
    val zippedData = data.zip(norms).map { case (v, norm) =>
      new VectorWithNorm(v, norm)
    }
    //调用runAlgorithm函数，实现K-Means算法，
    val model = runAlgorithm(zippedData)
    norms.unpersist()

    // Warn at the end of the run as well, for increased visibility.
    if (data.getStorageLevel == StorageLevel.NONE) {
      logWarning("The input data was not directly cached, which may hurt performance if its"
        + " parent RDDs are also uncached.")
    }
    model//返回模型
  }

  /**  * Implementation of K-Means algorithm.  */  private def runAlgorithm(data: RDD[VectorWithNorm]): KMeansModel = {

    val sc = data.sparkContext

    val initStartTime = System.nanoTime()

    // Only one run is allowed when initialModel is given
    val numRuns = if (initialModel.nonEmpty) {
      if (runs > 1) logWarning("Ignoring runs; one run is allowed when initialModel is given.")
      1
    } else {
      runs
    }

    //聚类中心初始化
    val centers = initialModel match {
      case Some(kMeansCenters) => {
        Array(kMeansCenters.clusterCenters.map(s => new VectorWithNorm(s)))
      }
      case None => {
        if (initializationMode == KMeans.RANDOM) {
          initRandom(data)
        } else {
          initKMeansParallel(data)
        }
      }
    }

    val initTimeInSeconds = (System.nanoTime() - initStartTime) / 1e9
    logInfo(s"Initialization with $initializationMode took " + "%.3f".format(initTimeInSeconds) +
      " seconds.")

    val active = Array.fill(numRuns)(true)
    val costs = Array.fill(numRuns)(0.0)

    var activeRuns = new ArrayBuffer[Int] ++ (0 until numRuns)
    var iteration = 0

    val iterationStartTime = System.nanoTime()

    // Execute iterations of Lloyd's algorithm until all runs have converged
    //使用Lloyd算法
    //可以参考分析理论部分的5和6
    //同时可以对比一下matlab的算法
    //這里多了缓存，并行度的变量
    while (iteration < maxIterations && !activeRuns.isEmpty) {
      type WeightedPoint = (Vector, Long)
      def mergeContribs(x: WeightedPoint, y: WeightedPoint): WeightedPoint = {
        axpy(1.0, x._1, y._1)
        (y._1, x._2 + y._2)
      }

      val activeCenters = activeRuns.map(r => centers(r)).toArray
      val costAccums = activeRuns.map(_ => sc.accumulator(0.0))

      val bcActiveCenters = sc.broadcast(activeCenters)

      // Find the sum and count of points mapping to each center
      //理论分析的第五部分，对每个中心到各自的样本的距离进行计算
      val totalContribs = data.mapPartitions { points =>
        val thisActiveCenters = bcActiveCenters.value
        val runs = thisActiveCenters.length
        val k = thisActiveCenters(0).length
        val dims = thisActiveCenters(0)(0).vector.size

        val sums = Array.fill(runs, k)(Vectors.zeros(dims))
        val counts = Array.fill(runs, k)(0L)

        points.foreach { point =>
          (0 until runs).foreach { i =>
            val (bestCenter, cost) = KMeans.findClosest(thisActiveCenters(i), point)
            costAccums(i) += cost
            val sum = sums(i)(bestCenter)
            axpy(1.0, point.vector, sum)
            counts(i)(bestCenter) += 1
          }
        }

        //contribs = ((并行度，那个中心)，某个聚类中心到各自样本之和，那个并行度下的那个聚类中心)
        val contribs = for (i <- 0 until runs; j <- 0 until k) yield {
          ((i, j), (sums(i)(j), counts(i)(j)))
        }
        contribs.iterator
      }.reduceByKey(mergeContribs).collectAsMap()

      bcActiveCenters.unpersist(blocking = false)

      // Update the cluster centers and costs for each active run
      for ((run, i) <- activeRuns.zipWithIndex) {
        var changed = false  var j = 0
        while (j < k) {
          val (sum, count) = totalContribs((i, j))
          if (count != 0) {
            scal(1.0 / count, sum)
            val newCenter = new VectorWithNorm(sum)
            if (KMeans.fastSquaredDistance(newCenter, centers(run)(j)) > epsilon * epsilon) {
              changed = true  }
            centers(run)(j) = newCenter
          }
          j += 1
        }
        if (!changed) {
          active(run) = false  logInfo("Run " + run + " finished in " + (iteration + 1) + " iterations")
        }
        costs(run) = costAccums(i).value
      }

      activeRuns = activeRuns.filter(active(_))
      iteration += 1
    }

    val iterationTimeInSeconds = (System.nanoTime() - iterationStartTime) / 1e9
    logInfo(s"Iterations took " + "%.3f".format(iterationTimeInSeconds) + " seconds.")

    if (iteration == maxIterations) {
      logInfo(s"KMeans reached the max number of iterations: $maxIterations.")
    } else {
      logInfo(s"KMeans converged in $iteration iterations.")
    }

    val (minCost, bestRun) = costs.zipWithIndex.min

    logInfo(s"The cost for the best run is $minCost.")

    new KMeansModel(centers(bestRun).map(_.vector))
  }

  /**  * Initialize `runs` sets of cluster centers at random.  */  //随机的寻找K个聚类中心
  private def initRandom(data: RDD[VectorWithNorm])
  : Array[Array[VectorWithNorm]] = {
    // Sample all the cluster centers in one pass to avoid repeated scans
    val sample = data.takeSample(true, runs * k, new XORShiftRandom(this.seed).nextInt()).toSeq
    Array.tabulate(runs)(r => sample.slice(r * k, (r + 1) * k).map { v =>
      new VectorWithNorm(Vectors.dense(v.vector.toArray), v.norm)
    }.toArray)
  }

  /**  * Initialize `runs` sets of cluster centers using the k-means|| algorithm by Bahmani et al.  * (Bahmani et al., Scalable K-Means++, VLDB 2012). This is a variant of k-means++ that tries  * to find with dissimilar cluster centers by starting with a random center and then doing  * passes where more centers are chosen with probability proportional to their squared distance  * to the current cluster set. It results in a provable approximation to an optimal clustering.  *  * The original paper can be found at http://theory.stanford.edu/~sergei/papers/vldb12-kmpar.pdf.  */  //用K-Means++理论
  private def initKMeansParallel(data: RDD[VectorWithNorm])
  : Array[Array[VectorWithNorm]] = {
    // Initialize empty centers and point costs.
    val centers = Array.tabulate(runs)(r => ArrayBuffer.empty[VectorWithNorm])
    var costs = data.map(_ => Array.fill(runs)(Double.PositiveInfinity))

    // Initialize each run's first center to a random point.
    val seed = new XORShiftRandom(this.seed).nextInt()
    val sample = data.takeSample(true, runs, seed).toSeq
    val newCenters = Array.tabulate(runs)(r => ArrayBuffer(sample(r).toDense))

    /** Merges new centers to centers. */  def mergeNewCenters(): Unit = {
      var r = 0
      while (r < runs) {
        centers(r) ++= newCenters(r)
        newCenters(r).clear()
        r += 1
      }
    }

    // On each step, sample 2 * k points on average for each run with probability proportional
    // to their squared distance from that run's centers. Note that only distances between points
    // and new centers are computed in each iteration.
    var step = 0
    while (step < initializationSteps) {
      val bcNewCenters = data.context.broadcast(newCenters)
      val preCosts = costs
      costs = data.zip(preCosts).map { case (point, cost) =>
        Array.tabulate(runs) { r =>
          math.min(KMeans.pointCost(bcNewCenters.value(r), point), cost(r))
        }
      }.persist(StorageLevel.MEMORY_AND_DISK)
      val sumCosts = costs
        .aggregate(new Array[Double](runs))(
          seqOp = (s, v) => {
            // s += v
            var r = 0
            while (r < runs) {
              s(r) += v(r)
              r += 1
            }
            s
          },
          combOp = (s0, s1) => {
            // s0 += s1
            var r = 0
            while (r < runs) {
              s0(r) += s1(r)
              r += 1
            }
            s0
          }
        )

      bcNewCenters.unpersist(blocking = false)
      preCosts.unpersist(blocking = false)

      val chosen = data.zip(costs).mapPartitionsWithIndex { (index, pointsWithCosts) =>
        val rand = new XORShiftRandom(seed ^ (step << 16) ^ index)
        pointsWithCosts.flatMap { case (p, c) =>
          val rs = (0 until runs).filter { r =>
            rand.nextDouble() < 2.0 * c(r) * k / sumCosts(r)
          }
          if (rs.length > 0) Some((p, rs)) else None
        }
      }.collect()
      mergeNewCenters()
      chosen.foreach { case (p, rs) =>
        rs.foreach(newCenters(_) += p.toDense)
      }
      step += 1
    }

    mergeNewCenters()
    costs.unpersist(blocking = false)

    // Finally, we might have a set of more than k candidate centers for each run; weigh each
    // candidate by the number of points in the dataset mapping to it and run a local k-means++
    // on the weighted centers to pick just k of them
    val bcCenters = data.context.broadcast(centers)
    val weightMap = data.flatMap { p =>
      Iterator.tabulate(runs) { r =>
        ((r, KMeans.findClosest(bcCenters.value(r), p)._1), 1.0)
      }
    }.reduceByKey(_ + _).collectAsMap()

    bcCenters.unpersist(blocking = false)

    val finalCenters = (0 until runs).par.map { r =>
      val myCenters = centers(r).toArray
      val myWeights = (0 until myCenters.length).map(i => weightMap.getOrElse((r, i), 0.0)).toArray
      LocalKMeans.kMeansPlusPlus(r, myCenters, myWeights, k, 30)
    }

    finalCenters.toArray
  }
}

KMeans同名对象

/**  * Top-level methods for calling K-means clustering.  */ @Since("0.8.0")
object KMeans {

  // Initialization mode names
  @Since("0.8.0")
  val RANDOM = "random"
  @Since("0.8.0")
  val K_MEANS_PARALLEL = "k-means||"

  /**  * Trains a k-means model using the given set of parameters.  *  * @param data Training points as an `RDD` of `Vector` types.  * @param k Number of clusters to create.  * @param maxIterations Maximum number of iterations allowed.  * @param runs Number of runs to execute in parallel. The best model according to the cost  * function will be returned. (default: 1)  * @param initializationMode The initialization algorithm. This can either be "random" or  * "k-means||". (default: "k-means||")  * @param seed Random seed for cluster initialization. Default is to generate seed based  * on system time.  */   @Since("1.3.0")
  //输入分类数据：data，聚类中心数目：k,最大迭代次数： maxIterations
  //并行数：runs（默认是1），初始化算法：initializationMode，种子：seed
  //一共6个参数
  def train(
             data: RDD[Vector],
             k: Int,
             maxIterations: Int,
             runs: Int,
             initializationMode: String,
             seed: Long): KMeansModel = {
    new KMeans().setK(k)
      .setMaxIterations(maxIterations)
      .internalSetRuns(runs)
      .setInitializationMode(initializationMode)
      .setSeed(seed)
      .run(data)
  }

  /**  * Trains a k-means model using the given set of parameters.  *  * @param data Training points as an `RDD` of `Vector` types.  * @param k Number of clusters to create.  * @param maxIterations Maximum number of iterations allowed.  * @param runs Number of runs to execute in parallel. The best model according to the cost  * function will be returned. (default: 1)  * @param initializationMode The initialization algorithm. This can either be "random" or  * "k-means||". (default: "k-means||")  */  @Since("0.8.0")
  //输入分类数据：data，聚类中心数目：k,最大迭代次数： maxIterations
  //并行数：runs（默认是1），初始化算法：initializationMode
  //一共5个参数
  def train(
             data: RDD[Vector],
             k: Int,
             maxIterations: Int,
             runs: Int,
             initializationMode: String): KMeansModel = {
    new KMeans().setK(k)
      .setMaxIterations(maxIterations)
      .internalSetRuns(runs)
      .setInitializationMode(initializationMode)
      .run(data)
  }

  /**  * Trains a k-means model using specified parameters and the default values for unspecified.  */  //输入分类数据：data，聚类中心数目：k,最大迭代次数： maxIterations

  //一共3个参数
  @Since("0.8.0")
  def train(
             data: RDD[Vector],
             k: Int,
             maxIterations: Int): KMeansModel = {
    train(data, k, maxIterations, 1, K_MEANS_PARALLEL)
  }

  /**  * Trains a k-means model using specified parameters and the default values for unspecified.  */  //输入分类数据：data，聚类中心数目：k,最大迭代次数： maxIterations
  //并行数：runs（默认是1）
  //一共4个参数
  @Since("0.8.0")
  def train(
             data: RDD[Vector],
             k: Int,
             maxIterations: Int,
             runs: Int): KMeansModel = {
    train(data, k, maxIterations, runs, K_MEANS_PARALLEL)
  }

  /**  * Returns the index of the closest center to the given point, as well as the squared distance.  */  //找出点到所有聚类中心最近的一个聚类中心，返回：(bestIndex, bestDistance)
  private[mllib] def findClosest(
                                  centers: TraversableOnce[VectorWithNorm],
                                  point: VectorWithNorm): (Int, Double) = {
    var bestDistance = Double.PositiveInfinity  var bestIndex = 0
    var i = 0
    centers.foreach { center =>
      // Since `\|a - b\| \geq |\|a\| - \|b\||`, we can use this lower bound to avoid unnecessary
      // distance computation.
      var lowerBoundOfSqDist = center.norm - point.norm
      lowerBoundOfSqDist = lowerBoundOfSqDist * lowerBoundOfSqDist
      if (lowerBoundOfSqDist < bestDistance) {
        val distance: Double = fastSquaredDistance(center, point)
        if (distance < bestDistance) {
          bestDistance = distance
          bestIndex = i
        }
      }
      i += 1
    }
    (bestIndex, bestDistance)
  }
  /**  * Returns the K-means cost of a given point against the given cluster centers.  */  //计算样本点和和中心点之间的距离
  private[mllib] def pointCost(
                                centers: TraversableOnce[VectorWithNorm],
                                point: VectorWithNorm): Double =
    findClosest(centers, point)._2

  /**  * Returns the squared Euclidean distance between two vectors computed by  * [[org.apache.spark.mllib.util.MLUtils#fastSquaredDistance]].  */  //返回两个点的2范数（距离）
  private[clustering] def fastSquaredDistance(
                                               v1: VectorWithNorm,
                                               v2: VectorWithNorm): Double = {
    MLUtils.fastSquaredDistance(v1.vector, v1.norm, v2.vector, v2.norm)
  }
  //验证初始化模型
  private[spark] def validateInitMode(initMode: String): Boolean = {
    initMode match {
      case KMeans.RANDOM => true  case KMeans.K_MEANS_PARALLEL => true  case _ => false  }
  }
}
KMeansModel
/**  * A vector with its norm for fast distance computation.  *  * @see [[org.apache.spark.mllib.clustering.KMeans#fastSquaredDistance]]
  */ private[clustering]
//自己定义
class VectorWithNorm(val vector: Vector, val norm: Double) extends Serializable {

  def this(vector: Vector) = this(vector, Vectors.norm(vector, 2.0))

  def this(array: Array[Double]) = this(Vectors.dense(array))

  /** Converts the vector to a dense vector. */  def toDense: VectorWithNorm = new VectorWithNorm(Vectors.dense(vector.toArray), norm)
}

KMeansModel类

class KMeansModel @Since("1.1.0") (@Since("1.0.0") val clusterCenters: Array[Vector])
  extends Saveable with Serializable with PMMLExportable {

  /**  * A Java-friendly constructor that takes an Iterable of Vectors.  */  @Since("1.4.0")
  def this(centers: java.lang.Iterable[Vector]) = this(centers.asScala.toArray)

  /**  * Total number of clusters.  */  @Since("0.8.0")
  def k: Int = clusterCenters.length

  /**  * Returns the cluster index that a given point belongs to.  */  @Since("0.8.0")
  def predict(point: Vector): Int = {
    KMeans.findClosest(clusterCentersWithNorm, new VectorWithNorm(point))._1
  }

  /**  * Maps given points to their cluster indices.  */  @Since("1.0.0")
  def predict(points: RDD[Vector]): RDD[Int] = {
    val centersWithNorm = clusterCentersWithNorm
    val bcCentersWithNorm = points.context.broadcast(centersWithNorm)
    points.map(p => KMeans.findClosest(bcCentersWithNorm.value, new VectorWithNorm(p))._1)
  }

  /**  * Maps given points to their cluster indices.  */  @Since("1.0.0")
  def predict(points: JavaRDD[Vector]): JavaRDD[java.lang.Integer] =
    predict(points.rdd).toJavaRDD().asInstanceOf[JavaRDD[java.lang.Integer]]

  /**  * Return the K-means cost (sum of squared distances of points to their nearest center) for this  * model on the given data.  */  @Since("0.8.0")
  def computeCost(data: RDD[Vector]): Double = {
    val centersWithNorm = clusterCentersWithNorm
    val bcCentersWithNorm = data.context.broadcast(centersWithNorm)
    data.map(p => KMeans.pointCost(bcCentersWithNorm.value, new VectorWithNorm(p))).sum()
  }

  private def clusterCentersWithNorm: Iterable[VectorWithNorm] =
    clusterCenters.map(new VectorWithNorm(_))

  @Since("1.4.0")
  override def save(sc: SparkContext, path: String): Unit = {
    KMeansModel.SaveLoadV1_0.save(sc, this, path)
  }

  override protected def formatVersion: String = "1.0"
}

KMeansModel同名对象

object KMeansModel extends Loader[KMeansModel] {

  @Since("1.4.0")
  override def load(sc: SparkContext, path: String): KMeansModel = {
    KMeansModel.SaveLoadV1_0.load(sc, path)
  }

  private case class Cluster(id: Int, point: Vector)

  private object Cluster {
    def apply(r: Row): Cluster = {
      Cluster(r.getInt(0), r.getAs[Vector](1))
    }
  }

  private[clustering]
  object SaveLoadV1_0 {

    private val thisFormatVersion = "1.0"

    private[clustering]
    val thisClassName = "org.apache.spark.mllib.clustering.KMeansModel"

    def save(sc: SparkContext, model: KMeansModel, path: String): Unit = {
      val sqlContext = SQLContext.getOrCreate(sc)
      import sqlContext.implicits._
      val metadata = compact(render(
        ("class" -> thisClassName) ~ ("version" -> thisFormatVersion) ~ ("k" -> model.k)))
      sc.parallelize(Seq(metadata), 1).saveAsTextFile(Loader.metadataPath(path))
      val dataRDD = sc.parallelize(model.clusterCenters.zipWithIndex).map { case (point, id) =>
        Cluster(id, point)
      }.toDF()
      dataRDD.write.parquet(Loader.dataPath(path))
    }

    def load(sc: SparkContext, path: String): KMeansModel = {
      implicit val formats = DefaultFormats
      val sqlContext = SQLContext.getOrCreate(sc)
      val (className, formatVersion, metadata) = Loader.loadMetadata(sc, path)
      assert(className == thisClassName)
      assert(formatVersion == thisFormatVersion)
      val k = (metadata \ "k").extract[Int]
      val centroids = sqlContext.read.parquet(Loader.dataPath(path))
      Loader.checkSchema[Cluster](centroids.schema)
      val localCentroids = centroids.rdd.map(Cluster.apply).collect()
      assert(k == localCentroids.length)
      new KMeansModel(localCentroids.sortBy(_.id).map(_.point))
    }
  }
}

SparkML实验

note:为了方便处理，这个数据和只是Matlab中的3，4列，而且是纯数字

package Cluster

import org.apache.spark.mllib.clustering.{KMeans, KMeansModel}
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.{SparkConf, SparkContext}

 object myKmean {
  def main(args: Array[String]) {
    val conf = new SparkConf().setAppName("KMeansExample").setMaster("local")
    val sc = new SparkContext(conf)
    
    // Load and parse the data
    val data = sc.textFile("C:\\Users\\andrew\\Desktop\\kmeans\\IrisData.txt")
    println(data)
    data.collect.foreach(println)
    val parsedData = data.map(s => Vectors.dense(s.split('\t').map(_.toDouble)))
    parsedData.collect.foreach(println)
    
    // Cluster the data into two classes using KMeans
    val initMode = "K-means||"
    val numClusters = 3
    val numIterations = 20
    val clusters = KMeans.train(parsedData, numClusters, numIterations,1,initMode)
    clusters.clusterCenters.foreach(println)
    //聚类中心的坐标
    //[5.595833333333332,2.0374999999999988]
    //[1.462,0.24599999999999994]
    //[4.269230769230769,1.3423076923076924]
    
    // Evaluate clustering by computing Within Set Sum of Squared Errors
    val WSSSE = clusters.computeCost(parsedData)
    println("Within Set Sum of Squared Errors = " + WSSSE)
    //Within Set Sum of Squared Errors = 31.371358974359016

    // Save and load model
    clusters.save(sc, "target/org/apache/spark/KMeansExample/KMeansModel")
    val sameModel = KMeansModel.load(sc, "target/org/apache/spark/KMeansExample/KMeansModel")


    sc.stop()

  }
}

对比于matlab的聚合中心

centers =
    2.0478    5.6261
    0.2460    1.4620
    1.3593    4.2926

    //聚类中心的坐标
    [5.595833333333332,2.0374999999999988]
    [1.462,0.24599999999999994]
    [4.269230769230769,1.3423076923076924]