矩阵乘法的经典题目_源自Matrix67_

嘛，都刷一遍好辣。
矩阵 Am∗n 就是一个m行n列的数表。
考虑矩阵的乘法：

C=A∗B=∑aik∗bkj

那么对于矩阵A的要求就是：A为m * n的矩阵
对于矩阵B的要求就是：B为n * p的矩阵
乘得的矩阵C的规模：m * p的矩阵
矩阵乘法是不满足交换律的。但它满足结合律和分配律。

经典题目1 给定n个点，m个操作，构造O(m+n)的算法输出m个操作后各点的位置。操作有平移、缩放、翻转和旋转
然后盗图

考虑实际上这个变换对应着一个类似于线性变换的东西，我们显然是可以用矩阵来搞的。
而对于翻转，旋转和缩放都是线性变换。
然而这里冒出一个平移。。
来想一想，发现肯定是多一维常量，这样就好了。
我们考虑一个向量 a⃗  经过矩阵的变换：

a⃗ =OPi∗a⃗ 

考虑这个矩阵的操作次序，一定是需要 左乘。
先翻转再平移和先平移再翻转肯定是不一样的。

#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#define Rep(i,n) for(int i = 1;i <= n;i ++)
#define PI M_PI
using namespace std;
int n,m;
struct Mat{double a[4][4];}p[10005];
Mat operator*(Mat w,Mat ww)
{
    Mat c;
    Rep(i,3)Rep(j,3)c.a[i][j] = 0;
    Rep(i,3)Rep(k,3)Rep(j,3)c.a[i][j] += w.a[i][k] * ww.a[k][j];
    return c;
}
int main ()
{
    scanf("%d%d",&n,&m);
    Rep(i,n)
        scanf("%lf%lf",&p[i].a[1][1],&p[i].a[2][1]),p[i].a[3][1] = 1.0;
    Mat res;
    Rep(i,3)Rep(j,3)res.a[i][j] = (i == j);
    Rep(i,m)
    {
        getchar();
        char op;
        scanf("%c",&op);
        Mat ori;
        Rep(i,3)Rep(j,3)ori.a[i][j] = (i == j);
        if(op == 'M')
        {
            double x,y; 
            scanf("%lf%lf",&x,&y);
            ori.a[1][3] = x;ori.a[2][3] = y;
        }
        else if(op == 'X')ori.a[2][2] = -1;
        else if(op == 'Y')ori.a[1][1] = -1;
        else if(op == 'S'){double S;scanf("%lf",&S);ori.a[1][1] = ori.a[2][2] = S;}
        else 
        {
            double ang;
            scanf("%lf",&ang);
            ang = ang / 180.0 * PI;
            ori.a[1][1] = cos(ang);
            ori.a[1][2] = - sin(ang);
            ori.a[2][1] = sin(ang);
            ori.a[2][2] = cos(ang);
        }
        res = ori * res;
    }
    Rep(i,n)p[i] = res * p[i],printf("%.1f %.1f\n",p[i].a[1][1],p[i].a[2][1]);
    return 0;
}

经典题目2 给定矩阵A，请快速计算出A^n（n个A相乘）的结果，输出的每个数都mod p。
考虑快速幂，那么实际上和乘法运算无异。（代码肯定以后要用得上）

经典题目3:
给定矩阵A，求

∑i=1kAi mod M

其中 k<=109 。
分治思想的应用，你可以很简单的发现： Ap 这种形式是可以通过快速幂计算的。
根据分治的思想，我们把k个和拆成前后两部分。

#include <cstdio>
#include <cstring>
#include <algorithm>
#define Rep(i,n) for(int i = 1;i <= n;i ++)
using namespace std;
int n,m,K,clu;
struct Matrix{int w[55][55];Matrix(){Rep(i,clu)Rep(j,clu)w[i][j] = (i == j);}};
Matrix A;
Matrix operator+ (Matrix a,Matrix b)
{
    Rep(i,clu)Rep(j,clu)a.w[i][j] = (a.w[i][j] + b.w[i][j]) % m;
    return a;
}
Matrix operator* (Matrix a,Matrix b)
{
    Matrix c;
    memset(c.w,0,sizeof(c.w));
    Rep(i,clu)Rep(k,clu)Rep(j,clu)c.w[i][j] = (c.w[i][j] + 1ll * a.w[i][k] * b.w[k][j]) % m;
    return c;
}
void print(Matrix a)
{
    puts("PRINT");
    Rep(i,clu){Rep(j,clu - 1)printf("%d ",a.w[i][j]);printf("%d\n",a.w[i][clu]);}
    puts("END");
}
Matrix FP(Matrix a,int p)
{
    Matrix c = Matrix();
    while(p)
    {
        if(p & 1)c = c * a;
        p >>= 1;
        a = a * a;
    }
    return c;
}
Matrix solve(int r)
{
    if(r == 1)return A;
    int mid = r >> 1;
    Matrix lm,rm;
    lm = solve(mid);
    rm = FP(A,mid) * lm;
    return r & 1 ? lm + rm  + FP(A,r) : lm + rm;
}
int main ()
{
    scanf("%d%d%d",&clu,&K,&m);
    Rep(i,clu)Rep(j,clu)scanf("%d",&A.w[i][j]);
    Matrix ans = solve(K);
    Rep(i,clu){Rep(j,clu - 1)printf("%d ",ans.w[i][j]);printf("%d\n",ans.w[i][clu]);}
    return 0;
}

经典题目4：送给圣诞夜的礼品
题意：
n个物品分别标号为1-n。顺次给出m个置换，反复使用这m个置换对初始序列进行操作，问k次置换后的序列。n<= 100,m<=10, k<2^31。
考虑到我们可以用矩阵来写出变换的形式：
即如果i会变换到j那么在矩阵上就将 aji 设为 1 。
考虑这个矩阵左乘一个列向量 A={p1,p2,p3,p4,p5,...}
那么乘完之后会得到一个列向量，它就是变换之后的局面。
想一想为什么会得到那个变换后的列向量c:
cij=∑aik∗bkj其中，aik中只有一个值是一，设其对应的列为p。
则有 cij=∑aip∗bpj
并且j只能取1，所以会发现向量c的第i个值等于向量b的第p个值。
考虑朴素做法：
设当前局面为P，则经过 opi 之后会得到的局面 C=opi∗P
我们已知会对C再经过一次操作 opi+1，C′=opi+1∗C
这样的话我们对op分组。
即把m个分为1组，然后依次左乘操作序列。
剩下k mod m个我们暴力即可。

#include <cstdio>
#include <cstring>
#include <algorithm>
#define Rep(i,n) for(int i = 1;i <= n;i ++)
using namespace std;
const int N = 105;
struct Matrix{int cl,rw,w[N][N];Matrix(){memset(w,0,sizeof(w));rw = cl = 0;}}op[15];
Matrix I(int cl){Matrix c;c.cl = c.rw = cl;Rep(i,cl)c.w[i][i] = 1;return c;}
Matrix operator*(Matrix a,Matrix b)
{
 Matrix c;
 c.rw = a.rw,c.cl = b.cl;
 Rep(i,a.rw)
 Rep(k,a.cl)
 Rep(j,b.cl)
 c.w[i][j] += a.w[i][k] * b.w[k][j];
 return c;
}
Matrix operator+(Matrix a,Matrix b){Rep(i,a.rw)Rep(j,a.cl)a.w[i][j] += b.w[i][j];return a;}
Matrix FP(Matrix a,int p)
{
 Matrix c = I(a.cl);
 while(p)
 {
 if(p & 1)c = c * a;
 p >>= 1;
 a = a * a;
 }
 return c;
}
int n,m,K;
Matrix ans,A;
void print(Matrix c){printf("%d %d\n",c.rw,c.cl);Rep(i,c.rw){Rep(j,c.cl)printf("%d ",c.w[i][j]);puts("");}}
int main ()
{
 scanf("%d%d%d",&n,&m,&K);
 ans.cl = 1;ans.rw = n;
 A.cl = A.rw = n;
 A = I(n);
 Rep(i,n)ans.w[i][1] = i;
 int p = K / m;
 Rep(i,m)
 {
 Matrix c;
 c.cl = c.rw = n;
 Rep(j,n)
 {
 int ww;
 scanf("%d",&ww); //把ww放到j上 
 c.w[j][ww] = 1;
 }
 op[i] = c;
 A = c * A;
 }
 A = FP(A,p);
 p = K % m;
 Rep(i,p)A = op[i] * A;
 A = A * ans;
 Rep(i,n - 1)printf("%d ",A.w[i][1]);printf("%d ",A.w[n][1]);puts("");
 return 0;
}

经典题目5：
经典题目5 《算法艺术与信息学竞赛》207页（2.1代数方法和模型，[例题5]细菌，版次不同可能页码有偏差）
大家自己去看看吧，书上讲得很详细。解题方法和上一题类似，都是用矩阵来表示操作，然后二分求最终状态。
这个没法写了。。下一题

经典题目6 给定n和p，求第n个Fibonacci数mod p的值，n不超过2^31
我们考虑到Fibonacci数列的递推公式： Fn=Fn−1+Fn−2
递推的话肯定会死得很惨，但是仔细想想，我们可以认为：
我们想得到一个矩阵，使得：
[a,b] * A = [b + a,a]
然后我们肯定就能构造Fibonacci的转移矩阵了。。
我们发现对于任意的线性递推，都可以用矩阵乘法优化。
形如F(n) = qF(n - 1) + pF(n - 2) + k（k为常量）;
那么我们可以画出矩阵：

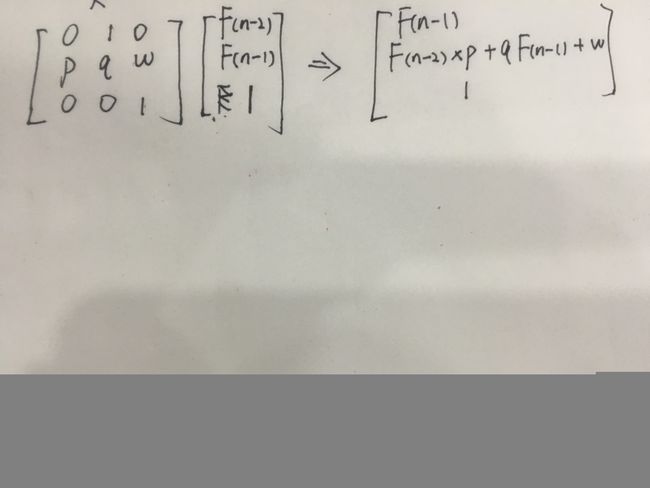
这样就可以优化线性递推了。
矩阵的构造方法为：在右上角的(k - 1)*(k - 1)的小矩阵中的主对角线上填1，矩阵第k行填对应的系数，其它地方都填0。
如果是加一个常量，那么就再扩大一行和一列，在(k - 1,k)这个位置写常量的系数，在(k,k)的位置写1，剩下都写0。

经典题目7 VOJ1067
dp转移很好写，再加上上面的矩阵乘法的优化知识，我们可以很轻松的做出这道题（早就做出来了）

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <queue>
#include <cmath>
#define Rep(i,n) for(int i = 1; i <= n ;i ++)
#define RD(i,l,r) for(int i = l;i <= r;i ++)
#define Repd(i,n) for(int i = n;i > 0 ;i --)
#define Rep_0(i,n) for(int i = 0;i < n;i ++)
#define RepG(i,x) for(int i = head[x]; ~ i;i = edge[i].next)
using namespace std;
typedef long long ll;
const int MOD = 7777777;
int n,m;
struct Matrix{ll f[12][12];};
Matrix operator*(Matrix a,Matrix b)
{
    int sz = m;
    Matrix c;memset(c.f,0,sizeof(c.f));
    Rep(i,sz)
        Rep(k,sz)
            Rep(j,sz)
                c.f[i][j] += a.f[i][k] * b.f[k][j],
                c.f[i][j] %= MOD;
    return c;
}
int read(){
    char ch = getchar();
    int x = 0;
    bool flag = 0;
    while(ch != '-' &&(ch < '0' || ch > '9'))ch = getchar();
    if(ch == '-')ch = getchar(),flag = 1;
    while(ch >= '0' && ch <= '9')x = 10 * x + ch - '0',ch = getchar();
    return flag ? -x : x;
}
/* f[n] = f[n - 1] + f[n - 2] + f[n - 3] + f[n - 4] + f[n - 5]; |0 1 0 0 0 | |f[n - 1]| |f[n - 2]| |0 0 1 0 0 | |f[n - 2]| |f[n - 3]| |0 0 0 1 0 | * |f[n - 3]| = |f[n - 4]| //左乘 |0 0 0 0 1 | |f[n - 4]| |f[n - 5]| |1 1 1 1 1 | |f[n - 5]| | f[ n ] | //正确性显然. //当然还有一种方法是倒着写: |1 1 1 1 1 | |f[n - 1]| | f[ n ] | |1 0 0 0 0 | |f[n - 2]| |f[n - 2]| |0 1 0 0 0 | * |f[n - 3]| = |f[n - 3]| //左乘 |0 0 1 0 0 | |f[n - 4]| |f[n - 4]| |0 0 0 1 0 | |f[n - 5]| |f[n - 5]| */

int main (){
    m = read(),n = read();
    Matrix a,b;
    memset(a.f,0,sizeof(a.f));
    memset(b.f,0,sizeof(b.f));
    a.f[1][1] = 1;
    RD(i,2,m)
        a.f[i][i - 1] = a.f[1][i] = 1;
    b.f[1][1] = 1;
    while(n)
    {
        if(n & 1)b = a * b;
        a = a * a;
        n >>= 1;
    }
    printf("%lld\n",b.f[1][1]);
    return 0;
}

经典题目8 给定一个有向图，问从A点恰好走k步（允许重复经过边）到达B点的方案数mod p的值
把给定的图转为邻接矩阵，即A(i,j)=1当且仅当存在一条边i->j。令 C=A∗A，那么C(i,j)=ΣA(i,k)∗A(k,j) ，实际上就等于从点i到点j恰好经过2条边的路径数（枚举k为中转点）。类似地，C*A的第i行第j列就表示从i到j经过3条边的路径数。同理，如果要求经过k步的路径数，我们只需要求出 Ak 即可。
首先这个正确性是很对的。
然后这样的话就根本不用讲了，快速幂解决即可。

经典题目9 用1 x 2的多米诺骨牌填满M x N的矩形有多少种方案，M<=5，N<2^31，输出答案mod p的结果

经典题目10 POJ2778
AC自动机+矩阵乘法优化，这里因为自己不会AC自动机。。。
所以留坑。