组合数学训练 (16.03.29)

复习组合数学的知识，本文主要涉及到母函数，catalan数，容斥原理，排列去重的内容。四道题：
hdu 1023 Train Problem II
hdu 5651 xiaoxin juju needs help
hdu 1023 Train Problem II
uva 11806 Cheerleaders

hdu 2082 找单词（母函数）

http://acm.hdu.edu.cn/showproblem.php?pid=2082
题目：假设有x1个字母A， x2个字母B,….. x26个字母Z，同时假设字母A的价值为1，字母B的价值为2,….. 字母Z的价值为26。那么，对于给定的字母，可以找到多少价值<=50的单词呢？单词的价值就是组成一个单词的所有字母的价值之和，比如，单词 ACM的价值是1+3+14=18，单词HDU的价值是8+4+21=33。(组成的单词与排列顺序无关，比如ACM与CMA认为是同一个单词）。

分析：
砝码背景问题：m=1g的砝码有2个，m=2的砝码有3个，那么组成总质量为6克的方案数有多少个？
   (1+x+x2)(1+x2+x4+x6)=1+x+2x2+x3+2x4+x5+2x6+x7+x8

同样，本题的解决方案是母函数。最终的结果就是母函数展开式中
 ∑i=150ai
其中 ai 是 xi 的对应系数

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int c1[55],c2[55];
int main()
{
    int t,p;
    cin>>t;
    while(t--){
        memset(c1,0,sizeof(c1));
        memset(c2,0,sizeof(c2));
        c1[0]=1;
        for(int i=1;i<=26;i++){
            scanf("%d",&p);
            if(p==0)  continue;
            for(int j=0;j<=50;j++){
                for(int k=0;k<=p&&k*i+j<=50;k++){  // k start at 0
                    c2[k*i+j]+=c1[j];  // dex is pow, value is constant
                }
            }
            for(int j=0;j<=50;j++) {
                c1[j]=c2[j];
                c2[j]=0;
            }
        }
        int ans=0;
        for(int i=1;i<=50;i++) ans=ans+c1[i];
        printf("%d\n",ans);
    }
    return 0;
}

hdu 5651 xiaoxin juju needs help（组合、去重）

http://acm.hdu.edu.cn/showproblem.php?pid=5651
大意：将一个字符串转化成回文字符串。方法——随意变化字符的位置
分析：
讨论不能构成回文字串的情况：
如果字符串长度是奇数，那么原串中出现次数是奇数的字符的个数只能有1个，否则不能构成回文字符。
如果字符串的长度是偶数，那么原串中出现次数是奇数的字符的个数必为0，否则不能构成回文字符。
有结果的情况：
把原串一刀切成两半，一半的长度是 ⌊length2⌋
设每一个字符的出现次数是 f(i)
那么由组合数学的知识（全排列和去重），答案就是： (∑f(i)2)!∏(f(i)2)!

可以使用逆元将除法转化成乘法。

#include <cstdio>
#include <iostream>
#include <cstring>
using namespace std;
typedef long long LL;
const LL mod=1e9+7,N=1e3+10;
char s[N];
LL f[30];
LL g[N];
void exgcd(LL a,LL b,LL &x,LL &y){
    if(b==0){
        x=1;  y=0;  return ;
    }
    exgcd(b,a%b,x,y);
    LL t=x;
    x=y;
    y=t-a/b*y;
}
int main(){
    g[0]=g[1]=1;
    for(LL i=2;i<N;i++) g[i]=g[i-1]*i%mod;
    int t;
    cin>>t;
    while(t--){
        scanf("%s",s);
         memset(f,0,sizeof(f));
        int L=0,odd=0;
        for(int i=0;s[i];i++){
            f[s[i]-'a']++;
            L++;
        }
        for(int i=0;i<26;i++){
            if(f[i]&1) odd++;
        }
        if((L&1)==1 && odd>1) puts("0");
        else if((L&1)==0 && odd>0) puts("0");
        else {
             LL ans=1,sum=0;
             for(int i=0;i<26;i++){
                     sum+=f[i];
                     LL ni,y;
                     exgcd(g[f[i]>>1],mod,ni,y);
                     ni=(ni%mod+mod)%mod;
                     ans=ans*ni%mod;
             }
             sum>>=1;
             ans=ans*g[sum]%mod;
             cout<<ans<<endl;
        }
    }
    return 0;
}

hdu 1023 Train Problem II（catalan 数）

http://acm.hdu.edu.cn/showproblem.php?pid=1023
大意：火车进出站第二种情况。我们把火车进出站的序列分成两部分考虑的话，结果就是

dp[n]=∑i=1ndp[i]×dp[n−i]

这相当于从二维图像的原点走到(n,n)的方案数。即

Cn2n−Cn−12n=(2n)!n!n!(1−nn+1)=(2n)!n!n!1n+1=Cn2nn+1

如果理解不了这句话，请看： http://blog.csdn.net/thearcticocean/article/details/50553848
答案数据特别大：
100：
896519947090131496687170070074100632420837521538745909320
用java写

uva 11806 Cheerleaders（容斥）

大意：题目要求在一个矩形范围内安排K个人，每一条边都要求存在至少一个人，每一个角如果有人的话，那么相邻的两条边都算有人。正着计算几乎算不出（反正我算不出），于是反着计算。求出边上没有人的并集：这样的话，可以避开角落问题。（读题很重要，英语。。。）

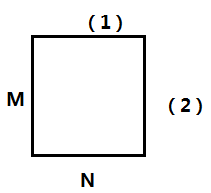
假设（1）没有人那么情况数有:
设一共k个人
L=M×N
sum=CkL−N
（2）近似分析 sum=CkL−M
设四条边没有人的情况数分别是 p1, p2, p3, p4
接下来用容斥原理求出所有边上无人的情况： p1⋃p2⋃p3⋃p4

p1=2ckL−m+2ckL−np2=ckL−2m+ckL−2n+4ckL−(m+n−1)p3=2ckL−(2m+n−2)+2ckL−(2n+m−2)p4=ckL−(2(m+n)−4)

并集用容斥原理求出。
最后用总的情况数减去这个并集即可。

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N=4e2+10,mod=1000007;
int c[N][N];
int main()
{
    memset(c,0,sizeof(c));
    c[0][0]=c[1][0]=c[1][1]=1;
    for(int i=2;i<N;i++) c[i][0]=c[i][i]=1;
    for(int i=2;i<N;i++){
        for(int j=1;j<i;j++){
            c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod;
        }
    }
    int t,ca=1;
    int m,n,k;
    cin>>t;
    while(t--){
        scanf("%d%d%d",&m,&n,&k);
        int ans=0,L=m*n;
        if(k>L || k==0) {
            printf("Case %d: 0\n",ca++);
            continue;
        }

        int p1=(2*c[L-m][k]%mod+2*c[L-n][k]%mod)%mod;
        int p2=(c[L-2*m][k]+c[L-2*n][k]+4*c[L-(m+n-1)][k]%mod)%mod;
        int p3=(2*c[L-(2*m+n-2)][k]%mod+2*c[L-(2*n+m-2)][k]%mod)%mod;
        int p4=c[L-(2*(m+n)-4)][k];

        ans=(c[L][k]-(p1-p2+p3-p4)%mod+mod)%mod;
        printf("Case %d: %d\n",ca++,ans);
    }
    return 0;
}

用二进制枚举写应该更加美。