笔试面试题目5
1. 删除字符分析: 转自《待字闺中》
删除字符串中的"b"和"ac",需要满足如下的条件:
1. 字符串只能遍历一次
2. 不能能够使用额外的空间
例如:
1. acbac ==> ""
2. aaac ==> aa
3. ababac ==> aa
4. bbbbd ==> d
进一步思考:如何处理aaccac呢,需要做那些改变?
思路:
使用状态机进行处理,我们有两个状态:ONE和TWO。TWO表示,前一个字符是'a'的状态,其他的都用ONE表示。
1. 如果当前状态为ONE,则拷贝:str[j]=str[i];但是如果当前字符满足以下两种状态中的任一个,则不进行拷贝
a. 当前字符是'b',因为我们要删除'b'
b. 当前字符是'a',我们要考虑下一个字符是c
2. 如果当前状态为TWO:
a. 当前字符不是'c',那么我们要首先拷贝前一个字符'a'
b. 然后考虑当前字符,如果不是'b'或者'a',则拷贝字符
状态转换非常简单,就是每次都检查是前一个字符为'a',基本代码如下:
void stringFilter( char * str)
{
// 初始状态为ONE,前一个字符不是'a'
int state = ONE;
int j = 0; // 初始化j为0
for(int i = 0; str[i] != '\0'; i++)
{
if(state == ONE && str[i] != 'a' && str[i] != 'b') // 当前状态为ONE的情况
{
str[j] = str[i];
j++;
}
if(state == TWO && str[i] != 'c') // 当前状态为ONE的情况
{
str[j] = 'a';
j++;
if(str[i] != 'a' && str[i] != 'b')
{
str[j] = str[i];
j++;
}
}
state = (str[i] == 'a') ? TWO : ONE;
}
if(state == TWO) // 这里容易忘记
{
str[j] = 'a';
j++;
}
str[j] = '\0';
}
进一步考虑aaccac时,最终得到ac,ac在题目中要求的也是要删除的。
如果题目要求将所有的ac删除,则需要做进一步的处理,对上述代码做一个简单修改即可。
在循环结束时,加入如下的代码:
if( j > 1 && str[j-2] == 'a' && str[j-1] == 'c')
{
j = j - 2;
}
例子代码:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
#define ONE 1
#define TWO 2
void stringFilter( char * str)
{
int state = ONE; // 初始状态为ONE,前一个字符不是'a'
int j = 0; // 初始化j为0
for(int i = 0; str[i] != '\0'; i++)
{
if(state == ONE && str[i] != 'a' && str[i] != 'b') // 当前状态为ONE的情况
{
str[j] = str[i];
j++;
}
if(state == TWO && str[i] != 'c') // 当前状态为TWO的情况
{
str[j] = 'a';
j++;
if(str[i] != 'a' && str[i] != 'b')
{
str[j] = str[i];
j++;
}
}
state = (str[i] == 'a') ? TWO : ONE;
// 根据题目要求,删除后再次组成ac是否需要删除
if( j > 1 && str[j-2] == 'a' && str[j-1] == 'c') // 删除后前后字符又组成了ac组合
{
j = j - 2;
}
}
if(state == TWO) // 这里容易忘记
{
str[j] = 'a';
j++;
}
str[j] = '\0';
}
int main()
{
char str[] = "acbac\0";
cout << str << " ==> ";
stringFilter(str);
cout << str << endl;
char str1[] = "aaccac\0";
cout << str1 << " ==> ";
stringFilter(str1);
cout << str1 << endl;
return 0;
}
运行结果:
acbac ==>
aaccac ==>
3. 不用除法求乘积:
两个数组,A[]与B[],其中B[]有如下的结果:
B[i] = A[0]*A[1]*...*A[i-1]*A[i+1]*...*A[n-1];
要求:
求B[i]的过程中,不允许使用除法,也不允许使用额外的空间。
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
void Multiply(int A[], int B[], int n)
{
int i = 0;
for( i = 0; i < n; i++)
{
B[i] = 1;
}
for( i = 1; i < n; i++)
{
B[i] = B[i-1]*A[i-1];
}
for( i = n-2; i >= 0; i--)
{
B[i] = B[i]*A[i+1];
A[i] = A[i]*A[i+1];
}
}
int main()
{
int A[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
int B[] = { 1, 1, 1, 1, 1, 1, 1, 1, 1, 1};
int multi = 1;
for(int i = 0; i < 10; i++)
{
multi *= A[i];
}
for(int i = 0; i < 10; i++)
{
cout << multi / A[i] << "\t";
}
Multiply(A, B, 10);
for(int i = 0; i < 10; i++)
{
cout << B[i] << "\t";
}
return 0;
} 输出结果:
3628800 1814400 1209600 907200 725760 604800 518400 453600 403200 362880
3628800 1814400 1209600 907200 725760 604800 518400 453600 403200 362880
4. 汽车加油是否可以回到出发点 转自:《待字闺中》
城市的环形路由n个加油站,第i个加油站的油量用gas[i]来表示,有如下的一辆车:
1. 它的油缸是无限量的,初始是空的。
2. 它从第i个加油站到i+1个加油站的消耗油量为cost[i]
现在你可以从任何加油站开始,路由加油站可以不断的加油,问是否能够走完环形路。如果可以返回开始加油站编号返回1,
否则返回-1.注意解决方案保证是唯一的。
其中一个问题需要理解:在第i站时,油缸中有的油量可以支撑你到第i+1站,对于每一站都要如此。而并不是你的总油量大于
总的耗油量就可以的。
暴力破解的方法:对每一个节点都试一下,然后找到每一站的油量都大于等于0的走法,返回开始的加油站。没有就返回-1。
时间复杂度为O(n^2)的时间复杂度。
优化:
上述的暴力破解方法中,我们可以看到有可以进行优化的地方。从第0个加油站开始,判断是否可以走完,然后从第1个加油站
开始判断,其实中间的计算已经做过了。反过来,我们用tank记录从0个站开始到某个站的油量。
考虑从第0个站开始,到该加油站的油量为 gas[i]-cost[i]+tank;这样时间复杂度可以是O(n),事实上确实如此:
tank表示当前车的油缸里的油量。
1. 从第0个站开始,tank+=gas[0]-cost[0],只要tank>=0,我们就继续到下一个加油站
2. 当不满足tank>=0时,顺着环路试着从下一个站开始,比如n-1: tank+=gas[n-1]-cost[n-1]。如果还小于0,继续实验再前一个
3. 知道满足tank>=0,在进行第一步依次类推。
4. 当一前一后这两个相遇了,算法也就结束了,tank>=0就成功,返回相遇的位置,否则失败,返回-1。
上述方法的时间复杂度是 O(n),作为一个整体来看,每一个阶段都直走了一次。
5. 连连看,判断两个图片之间是否可以连线(有条件)
对于连连看,当点击两个图标时,判断两个图标是否可以通过一条最多具有两个拐点的线连接起来,首先看一个例子。
如下图:
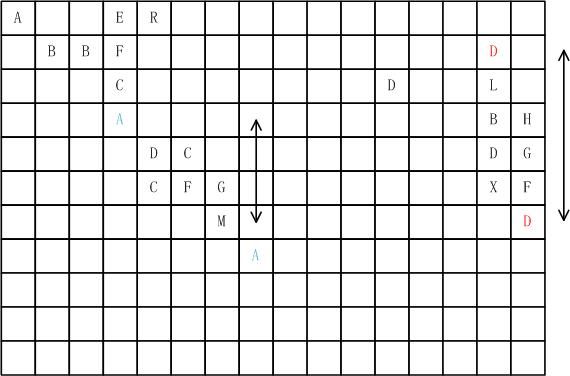
图中,两个绿色的A,我们可以通过两个途径测试是否两个A有满足条件的线存在。
以横坐标为例,在图中我们以两个A所在的位置(3,3)和(7,7)所在的位置纵坐标向两边扩展,如果是空白格则并进来,否则停止。
由此可以得到A(3,3)的空白格为[0-13],到A(7,7)的空白格为[0-15],以其中一个A(3,3)为基准,将其空白格集合逐格向外扩展,并与A(7,7)的空白格集合进行对比,例如(7,3)(7,7),分属两个集合的两个空白格之间有空白格通道,则说明找到了一条线。那么我们要得到的线就为 A(3,3) - (7,3) - A(7,7) ,中间经过了一个拐点(7,3)。
如果对于横坐标上没有想通空白格通道时,可以以相同的方法测试一下在纵坐标上是否有这样的通道。
对于出于边界的两个图片,如两个红色的D,我们可以通过箭头线所画路径连接消除。这里要做一个特殊的处理,就是在整个矩形周边留出一圈空白格,这样就可以很好地使用上述的方法进行解决。
6. 二叉树的sibling node:
有如下的结构体,其中的sibling字段指向本层节点的左边节点,如果没有则设置为NULL。
typedef struct _BiNode
{
struct _BiNode * left;
struct _BiNode * right;
struct _BiNode * sibling;
int value;
}BiNode; 例如:一个二叉树如下图所示,其对应的处理以后的如其下的图所示。
A
/ \
B C
/ \ \
D E G
/ / \
K J L
A
/ \
B <- C
/ \ \
D--E <- G
/ / \
K ---J <----- L
代码如下(未建立二叉树进行验证)
BiNode* ConnectSibling(BiNode * root)
{
if(root == NULL || (root->left == NULL && root->right == NULL))
{
return root;
}
BiNode* p = NULL;
vector<BiNode *> nodes;
nodes.push_back(root);
root->sibling = NULL;
int start = 0, end = 1, cur = 0;
while( start < end)
{
cur = start;
while(cur+1 < end)
{
nodes[cur+1]->sibling = nodes[cur];
cur ++;
}
cur = start;
while( cur < end)
{
p = nodes[cur]->left;
if( p != NULL)
{
nodes.push_back(p);
p->sibling = NULL;
}
p = nodes[cur]->right;
if( p != NULL)
{
nodes.push_back(p);
p->sibling = NULL;
}
cur++;
}
start = end; end = nodes.size();
}
return root;
} 7. 蛇形矩阵
输出蛇形矩阵,蛇形矩阵如下矩阵所示,使用两种方法实现蛇形矩阵的输出,空间复杂度分别为O(n^2) 和 O(1)
1 2 6 7
3 5 8 13
4 9 12 14
10 11 15 16
#define Num 5
void SnakeArray(int N)
{
int array[Num][Num];
int i = 0, j = 0, index = 1, n = 0;
for( int k = 0; k <= 2*(N-1); k++)
{
if( k > N-1)
{
n = k - (N-1);
}
if(k % 2 == 0)
{
i = k - n; j = k-i;
while( i >= n)
{
array[i][j] = index++;
i--; j++;
}
}
else if(k % 2 == 1)
{
j = k-n; i = k-j;
while( j >= n)
{
array[i][j] = index++;
j--; i++;
}
}
}
for(int i = 0; i < N; i++)
{
for(int j = 0; j < N; j++)
{
cout << array[i][j] << " ";
}
cout << endl;
}
return ;
} 8. N个有序单链表合并
有N个有序的单链表,将这N个有序的单链表合并为一个有序的单链表。
typedef struct _Node
{
struct _Node * next;
int value;
}Node;
Node * MergeLists(int N, Node* lists[])
{
if(N<=0 || lists == NULL)
return NULL;
if( N == 1)
{
return lists[0];
}
int k = 1;
Node * p = lists[0], *q = NULL, *r = NULL, *cur = NULL;
while( k < N)
{
q = p;
r = lists[k];
if( q->value < r->value)
{
p = cur = q;
q = q->next;
}
else
{
p = cur = r;
r = r->next;
}
while( q != NULL && p != NULL)
{
if( q->value < r->value)
{
cur->next = q;
cur = q;
q = q->next;
}
else
{
cur->next = r;
cur = r;
r = r->next;
}
}
if( q != NULL)
{
cur->next = q;
}
else if( r != NULL)
{
cur->next = r;
}
k++;
}
return p;
}
By Andy @ 2013年10月18日