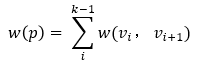图算法 单源最短路径 Dijkstra算法(邻接表/邻接矩阵+优先队列STL)
一、前言
最短路径算法,顾名思义就是求解某点到某点的最短的距离、消耗、费用等等,有各种各样的描述,在地图上看,可以说是图上一个地点到达另外一个地点的最短的距离。比方说,我们把地图上的每一个城市想象成一个点,从一个城市到另一个城市的花费是不一样的。现在我们要从上海去往北京,需要考虑的是找到一条路线,使得从上海到北京的花费最小。有人可能首先会想到,飞机直达啊,这当然是时间消耗最小的方法,但是考虑到费用的高昂,这条线路甚至还不如上海到北京的高铁可取。更有甚者,假设国家开通了从上海到西藏,再从西藏到兰州等等城市经过万般周折最后到达北京的一条线路,虽然要需要经历较长一段时间,但是价钱相比前二者非常实惠(假设只要一块钱,便能跑大半个中国,领略多省风光),单从省钱的角度看来,自然最后这条是可取的。这就是我们在这里所说的单源最短路径。我们接下来的篇幅中将去讲解所有边权值为非负的有向图的单源最短路径,由于无向图相当于变相的有向图,在这里就不做解释,留作读者自行推广。
二、概念
这里我们讲解最短路径,需要掌握几个基本的概念:
对于有向图G=(V,E),权值函数W: E→R(即每条边的权值都为一个实数)
1、路径
表示从v1到vk的一条路径,它的权值为:
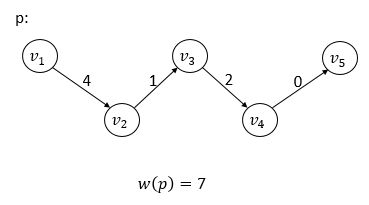
例:
2、最短路径:从u到v的一条路径,使w(p)最小,w(p)。
3、最短路径权值:
注意,最短路径可能不存在:
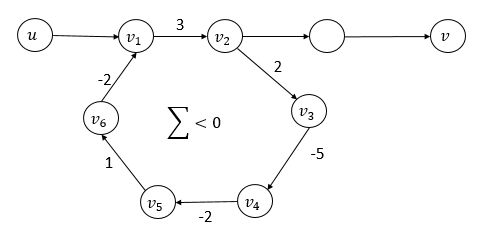
(1)存在负权回路,例如:
可以看出,存在v1到v6的负权回路,它的权值为-3,如果我们想找从u到v的最短路径,那么无限循环地走这个负权回路可以使最短路径越来越小,最后达到负无穷, 那么就说明找不到从u到v的最短路径。
(2)不存在从u到v的路径,这个是肯定不会存在最短路径的。
三、最优子结构
我们不难发现,求解源点到某一顶点的最短路径,其实不比求解源点到所有顶点的路径简单。这个时候我们要引入全局的概念,能不能找出所有的顶点的最短路径,然后再去查看到目标点的最短路径呢?很多人就会想到动态规划这一思想,说道动态规划,自然我们首先要考虑的问题是最优子结构。
最短路径满足最优子结构性质:最短路径的子路径是最短路径。
证明:(剪贴法)
前提:u到v是最短路径。
假设:x到y不是最短路径,那么存在一条更短的路径从x到y(假设为下面的弯箭头),这样,删去原路径中从x到y的路径,用新找到的路径替代(弯箭头),那么就得到 了一条比u到v的权值更短的路径,这与前提u到v是最短路径相矛盾,因而x到y是最短路径,即最短路径满足最优子结构性质。
引入三角不等式的概念:(从u到v的最短路径权值,小于等于从u到x的最短路径权值加上从x到v的最短路径权值)
这个性质根据最优子结构性质而来,非常重要。
四、单元最短路径问题
对于图G= (V, E),给定源点s,找到从s到所有顶点v的最短路径。
由于在本文中我们讲解Dijkstra算法,需要假设没有负权值,即:
![]()
因而,只要路径存在,便存在最短路径。
五、Dijkstra算法思想
Dijkstra是非常非常著名的计算机科学家,可能很多人对他的了解只在他的单元最短路径算法上,对操作系统了解的人可能还了解他的银行家算法,在方法学领域还有goto有害论等等。当然要讲他的其他杰出贡献,那就要把话题扯远了,今天我们只讲讲Dijkstra算法的思想,然后在后面给出它的实现过程,必要的给出其正确性的证明(Dijkstra在程序正确性证明领域发明了最弱前置谓词证明方法,不过我们不会用他的方法证明他老人家的程序的正确性,不然就扯到了十万八千里-。-)。
算法思想:
(1)在任意时刻,我们都要得到从源点到所有顶点的估算距离,并维持一个顶点集合S,若顶点v在S中,则说明从源点到v的最短路径已知;
(2)在每一次将不在S中的顶点v加到S中去时,总是选择从源点到v的估算距离最小的;
(3)顶点v加入S中之后,对于所有与v相邻的顶点(不属于S),更新它们的估算距离。
由(2),我们看到了贪心的影子,在每次选择时,我们总是想选择花费最小的,正常人都会这样去想,至于为什么这样选,这样选对不对,我们将在后面进行证明。
伪代码如下:
1 Dijkstra(G, W, s) //G表示图,W表示权值函数,s表示源顶点 2 d[s] ←0 //源点到源点最短路为0 3 for each v ∈ V - {s} //3-8行均为初始化操作 4 do d[v]←∞ 5 parent[v]←NIL 6 S←∅ 7 Q←V //此处Q为优先队列,存储未进入S的各顶点以及从源点到这些顶点的估算距离,采用二叉堆(最小堆)实现,越小越优先 8 while Q≠∅ 9 do u←Extract-Min(Q) //提取估算距离最小的顶点,在优先队列中位于顶部,出队列,放入集合S中 10 S←S∪{u} 11 for each v ∈ Adj(u) //松弛操作,对与u相邻的每个顶点v,进行维持三角不等式成立的松弛操作。 12 do if d[v] > d[u] + w(u, v) 13 then d[v] = d[u] + w(u, v) //这一步隐含了更新优先队列中的值,DECREASE。 14 parent[v]←u //置v的前驱结点为u
六、简单例子说明
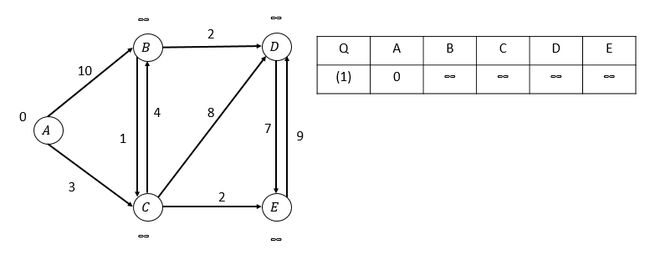
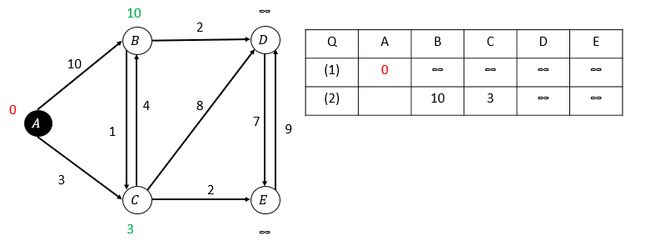
初始情况:
第一次松弛,选取A顶点:
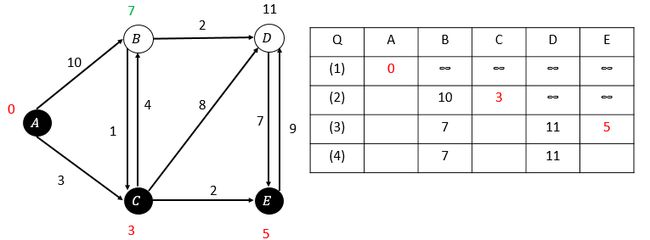
第二次松弛,C的估算距离最小,选取C顶点:
第三次松弛,E的估算距离最小,选取E:
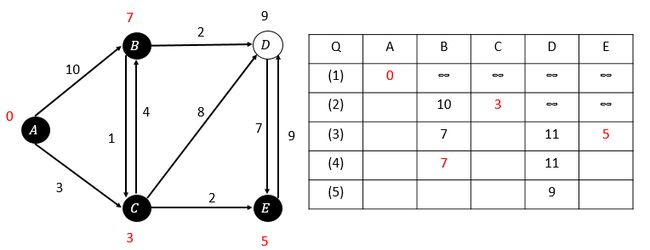
第四次松弛,B的估算距离最小,选取B:
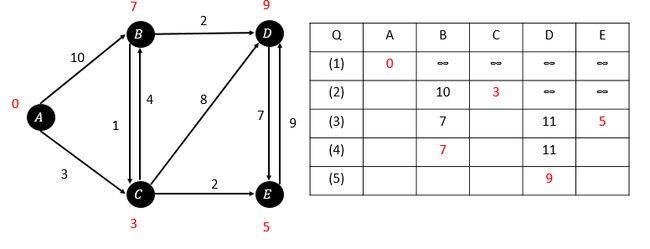
第五次松弛:(最后一个点,完成)
经过所有的松弛操作之后,我们就得到了所有顶点的最短路径(表格中红字部分)。
如果加上对parent[]进行的操作,我们还可以得到一棵最短路径树,这个读者可以自行推广。
七、代码实现
相比正确性,可能大家更加关注的是代码的实现,这里我们给出Dijkstra的实现代码,图结构的存储采用邻接矩阵和邻接表两种形式,有关图的表示方法,可以参看下面的博客:http://www.cnblogs.com/dzkang2011/p/graph_1.html。优先队列采用C++ 优先队列STL,priority_queue,由于无法直接更改队列中的值,我们需要对实现进行稍微的修改,这对最后结果不会产生影响,详情见代码。
1、邻接表C/C++:
#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
#define maxn 110 //最大顶点个数
int n; //顶点个数
struct arcnode //边结点
{
int vertex; //与表头结点相邻的顶点编号
int weight; //连接两顶点的边的权值
arcnode * next; //指向下一相邻接点
arcnode() {}
arcnode(int v,int w):vertex(v),weight(w),next(NULL) {}
};
struct vernode //顶点结点,为每一条邻接表的表头结点
{
int vex; //当前定点编号
arcnode * firarc; //与该顶点相连的第一个顶点组成的边
}Ver[maxn];
void Init() //建立图的邻接表需要先初始化,建立顶点结点
{
for(int i = 1; i <= n; i++)
{
Ver[i].vex = i;
Ver[i].firarc = NULL;
}
}
void Insert(int a, int b, int w) //尾插法,插入以a为起点,b为终点,权为w的边,效率不如头插,但是可以去重边
{
arcnode * q = new arcnode(b, w);
if(Ver[a].firarc == NULL)
Ver[a].firarc = q;
else
{
arcnode * p = Ver[a].firarc;
if(p->vertex == b)
{
if(p->weight > w)
p->weight = w;
return ;
}
while(p->next != NULL)
{
if(p->next->vertex == b)
{
if(p->next->weight > w);
p->next->weight = w;
return ;
}
p = p->next;
}
p->next = q;
}
}
void Insert2(int a, int b, int w) //头插法,效率更高,但不能去重边
{
arcnode * q = new arcnode(b, w);
if(Ver[a].firarc == NULL)
Ver[a].firarc = q;
else
{
arcnode * p = Ver[a].firarc;
q->next = p;
Ver[a].firarc = q;
}
}
struct node //顶点节点,保存id和到源顶点的估算距离,优先队列需要的类型
{
int id; //源顶点id和估算距离
int w;
friend bool operator<(node a, node b) //因要实现最小堆,按升序排列,因而需要重载运算符,重定义优先级,以小为先
{
return a.w > b.w;
}
};
#define INF 0xfffff //权值上限
int parent[maxn]; //每个顶点的父亲节点,可以用于还原最短路径树
bool visited[maxn]; //用于判断顶点是否已经在最短路径树中,或者说是否已找到最短路径
node d[maxn]; //源点到每个顶点估算距离,最后结果为源点到所有顶点的最短路。
priority_queue<node> q; //优先队列stl实现
void Dijkstra(int s) //Dijkstra算法,传入源顶点
{
for(int i = 1; i <= n; i++) //初始化
{
d[i].id = i;
d[i].w = INF; //估算距离置INF
parent[i] = -1; //每个顶点都无父亲节点
visited[i] = false; //都未找到最短路
}
d[s].w = 0; //源点到源点最短路权值为0
q.push(d[s]); //压入队列中
while(!q.empty()) //算法的核心,队列空说明完成了操作
{
node cd = q.top(); //取最小估算距离顶点
q.pop();
int u = cd.id;
if(visited[u]) //注意这一句的深意,避免很多不必要的操作
continue;
visited[u] = true;
arcnode * p = Ver[u].firarc;
//松弛操作
while(p != NULL) //找所有与他相邻的顶点,进行松弛操作,更新估算距离,压入队列。
{
int v = p->vertex;
if(!visited[v] && d[v].w > d[u].w+p->weight)
{
d[v].w = d[u].w+p->weight;
parent[v] = u;
q.push(d[v]);
}
p = p->next;
}
}
}
int main()
{
int m, a, b, c, st, ed;
printf("请输入顶点数和边数:\n");
scanf("%d%d", &n, &m);
printf("请输入边以及权值(a, b, c)\n");
Init(); //计算前必须初始化
while(m--)
{
scanf("%d%d%d", &a, &b, &c);
Insert2(a, b, c); //无向图注意存储两条边
Insert2(b, a, c);
}
printf("请输入起点和终点:\n");
scanf("%d%d", &st, &ed);
Dijkstra(st);
if(d[ed].w != INF)
printf("最短路径权值为:%d\n", d[ed].w);
else
printf("不存在从顶点%d到顶点%d的最短路径。\n", st, ed);
return 0;
}
2、邻接矩阵C/C++:
#include <iostream>
#include <cstdio>
#include <queue>
using namespace std;
#define maxn 110 //最大顶点个数
#define INF 0xffffff //权值上限
int w[maxn][maxn]; //邻接矩阵,存储权值
int n; //顶点个数
struct node //顶点节点,保存id和到源顶点的估算距离,优先队列需要的类型
{
int id, weight; //源顶点id和估算距离
friend bool operator<(node a, node b) //因要实现最小堆,按升序排列,因而需要重载运算符,重定义优先级,以小为先
{
return a.weight > b.weight;
}
};
priority_queue<node> q; //优先队列,最小堆,实现Dijkstra的重要数据结构,用stl实现
int parent[maxn]; //每个顶点的父亲节点,可以用于还原最短路径树
bool visited[maxn]; //用于判断顶点是否已经在最短路径树中,或者说是否已找到最短路径
node d[maxn]; //源点到每个顶点估算距离,最后结果为源点到所有顶点的最短路。
void Dijkstra(int s) //Dijkstra算法,传入源顶点
{
for(int i = 1; i <= n; i++) //初始化
{
d[i].id = i;
d[i].weight = INF; //估算距离置INF
parent[i] = -1; //每个顶点都无父亲节点
visited[i] = false;
}
d[s].weight = 0; //源点到源点最短路权值为0
q.push(d[s]); //压入队列中
while(!q.empty()) //算法的核心,队列空说明完成了操作
{
node cd = q.top(); //取最小估算距离顶点
q.pop();
int u = cd.id;
if(visited[u])
continue;
visited[u] = true;
//松弛操作
for(int v = 1; v <= n; v++) //找所有与他相邻的顶点,进行松弛操作,更新估算距离,压入队列。
{
if(v != u && !visited[v] && d[v].weight > d[u].weight+w[u][v])
{
d[v].weight = d[u].weight+w[u][v];
parent[v] = u;
q.push(d[v]);
}
}
}
}
int main()
{
int m, a, b, c, st, ed;
printf("请输入顶点数和边数:\n");
scanf("%d%d", &n, &m);
printf("请输入边以及权值(a, b, c)\n");
for(int i = 1; i <= n; i++) //邻接矩阵存储前需要初始化
for(int j = i; j <= n; j++)
w[i][j] = w[j][i] = INF;
while(m--)
{
scanf("%d%d%d", &a, &b, &c);
if(w[a][b] > c)
w[a][b]= w[b][a] = c;
}
printf("请输入起点和终点:\n");
scanf("%d%d", &st, &ed);
Dijkstra(st);
if(d[ed].weight != INF)
printf("最短路径权值为:%d\n", d[ed].weight);
else
printf("不存在从顶点%d到顶点%d的最短路径。\n", st, ed);
return 0;
}
八、时间复杂度分析
不管用什么方法,总共用时为O(V*T(EXTRACTION)+E*T(DECREASE))
(1)如果用数组来实现,总时间复杂度为O(V2)
(2)如果用二叉堆来实现,总时间复杂度为O(ElogV)
(3)如果使用斐波那契堆,总时间复杂度为O(E+VlogV)
上面的三种方法,越往下时间复杂度越好,但是实现难度越高,而且每次对最小优先队列的更新是非常麻烦的,那么,有没有一种方法,可以不更新优先队列也达到同样的 效果呢?
答案是:有。
其实只需要简单的操作就可以达到。首次只将根结点入队列。第一次循环,取出队列顶结点,将其退队列,之后找到队列顶的结点的所有相邻顶点,若有更新,则更新它们 的key值后,再将它们压入队列。重复操作直至队列空为止。因为对树的更新是局部的,所以只需将相邻顶点key值更新即可。push操作的复杂度为O(logV),而且省去了之前 将所有顶点入队列的时间,因而总复杂度为O(ElogV)。