ZOJ 3329 One Person Game (概率DP)
http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3329
题目:抛掷3个骰子(分别共有k1,k2,k3个点),如果对应的点数分别是a,b,c那么就变成0,累加加上点数之和,直到score>n时结束。问投掷3个骰子的次数。
做完这题发现,原来,一般的概率DP的设计都是从后向前推导。
设dp[i]是分数为i的次数期望,
p[i]是相关概率,有:
( i+k!=0 ) (1)
抽象成: (2)
(dp[i+k]含有dp[0],所以不能简单地认为a[0]就是p[0])
将 带入(1)计算,得到:
联系(2)得到:
这样一带一比就找到了a[i]和b[i]的递推式,很神奇啊有木有
当i=0时,有
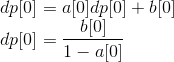
因为dp(i>n)=0,所以有 a[i>n]=b[i>n]=0。
最后求得dp[0]即可。
( i+k!=0 ) (1)
抽象成: (2)
(dp[i+k]含有dp[0],所以不能简单地认为a[0]就是p[0])
将 带入(1)计算,得到:
联系(2)得到:
这样一带一比就找到了a[i]和b[i]的递推式,很神奇啊有木有
当i=0时,有
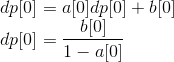
因为dp(i>n)=0,所以有 a[i>n]=b[i>n]=0。
最后求得dp[0]即可。
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int n,k1,k2,k3,A,B,C;
double a[505],b[505];
double p[20];
int main()
{
int t;
cin>>t;
while(t--){
scanf("%d%d%d%d%d%d%d",&n,&k1,&k2,&k3,&A,&B,&C);
double one=1.0/k1/k2/k3;
memset(p,0,sizeof(p));
for(int i=1;i<=k1;i++){
for(int j=1;j<=k2;j++){
for(int k=1;k<=k3;k++){
if(i==A&&j==B&&k==C) continue;
p[i+j+k]+=one;
}
}
}
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
for(int i=n;i>=0;i--){
a[i]=one; //p0
b[i]=1.0;
for(int j=3;j<=(k1+k2+k3);j++){
a[i]+=p[j]*a[i+j];
b[i]+=p[j]*b[i+j];
}
}
printf("%.15lf\n",b[0]/(1-a[0]));
}
return 0;
}