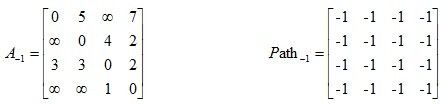Dijkstra算法总结
单源最短路径问题,即在图中求出给定顶点到其它任一顶点的最短路径。在弄清楚如何求算单源最短路径问题之前,必须弄清楚最短路径的最优子结构性质。
一.最短路径的最优子结构性质
该性质描述为:如果P(i,j)={Vi....Vk..Vs...Vj}是从顶点i到j的最短路径,k和s是这条路径上的一个中间顶点,那么P(k,s)必定是从k到s的最短路径。下面证明该性质的正确性。
假设P(i,j)={Vi....Vk..Vs...Vj}是从顶点i到j的最短路径,则有P(i,j)=P(i,k)+P(k,s)+P(s,j)。而P(k,s)不是从k到s的最短距离,那么必定存在另一条从k到s的最短路径P'(k,s),那么P'(i,j)=P(i,k)+P'(k,s)+P(s,j)<P(i,j)。则与P(i,j)是从i到j的最短路径相矛盾。因此该性质得证。
二.Dijkstra算法
由上述性质可知,如果存在一条从i到j的最短路径(Vi.....Vk,Vj),Vk是Vj前面的一顶点。那么(Vi...Vk)也必定是从i到k的最短路径。为了求出最短路径,Dijkstra就提出了以最短路径长度递增,逐次生成最短路径的算法。譬如对于源顶点V0,首先选择其直接相邻的顶点中长度最短的顶点Vi,那么当前已知可得从V0到达Vj顶点的最短距离dist[j]=min{dist[j],dist[i]+matrix[i][j]}。根据这种思路,
假设存在G=<V,E>,源顶点为V0,U={V0},dist[i]记录V0到i的最短距离,path[i]记录从V0到i路径上的i前面的一个顶点。
1.从V-U中选择使dist[i]值最小的顶点i,将i加入到U中;
2.更新与i直接相邻顶点的dist值。(dist[j]=min{dist[j],dist[i]+matrix[i][j]})
3.知道U=V,停止。
代码实现:
Dijkstra算法详解:
在解决单源点最短路径的问题时,常常用到经典的Dijkstra算法,其算法的本质思想是: 按路径长度递增依次产生最短路径。
下面给出算法的大致流程:
1.初始化所有结点并将起始点设为标记,进入以下循环
2.在到达某点的最短路径中找最小且未标记的点(可以用一维数组表示)
如:
数组下标:0 1 2 3 4 5
Len :- 0 5 10 2 -
这个数组表示 1号节点为初始节点,1号节点到达2号节点的最短路径为5,到3号为10,无法到达5号(具体可以以较大的数表示其路径)。
从中找到一个未标记且Len最短的一个,未标记用另一数组记录
如:
数组下标:0 1 2 3 4 5
标记 :0 1 0 0 1 0
此数组表示从初始节点到达4号节点的最短路径已找到
从以上两个数组中可以得出:此次循环找到的点为2号节点,进入下一步
3.标记找到的点,以此标记点为中间点重新计算所有未标记点的最短路径(更新最短路径表)
4.循环1.2步至n-1次(n为顶点数,若最后还有未被标记的,说明无法到达此点)
下面是核心代码:
<span style="font-size:32px;color:#3333ff;"> while(count<n)
{
tempmin=INFINITE;
for(i=1;i<=n;i++)
{
if(in[i]==0&&Len[i]<tempmin) //find the smallest one
{
tempmin=Len[i];
si=i;
}
}
in[si]=1;
count++;
for(i=1;i<=n;i++) //updata the length
{
if(in[i]==0&&(tempmin+mGraph.matrix[si][i])<Len[i])
{
Len[i]=tempmin+mGraph.matrix[si][i];
}
}
}</span>
核心部分是上面的两个for循环,第一个for循环遍历所有结点,找到未标记并且长度最短的路径;第二个for循环也是遍历所有结点以上面找到的最短路径结点为中间点更新最短路径表;注意在第一个for循环之后要标记找到的点(说明到达此点的最短路径已找到)
下面用一个实例来具体说明:
若有这样一张有向图(此图为《数据结构》严蔚敏 p188页,书中没有详细讲解,现以此为实例)
V0-V5 共6个节点,节点间路径已标出,现要求从V0到其余各节点的最短路径;
有上面的算法流程可知,在使用Dijkstra算法时需要几个结构来保存我们想要的信息:
1.保存这张图的结构体
2.记录V0到其余各节点最短路径的数组(这里设为Len[n+1])
3.记录某节点是否已找到最短路径的数组(这里设为in[n+1])
接下来就是算法实现部分:
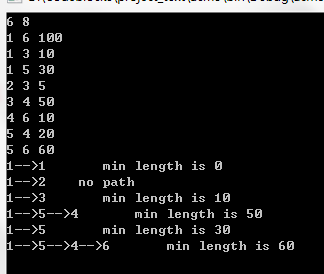
1.标记V0 -- in[1]=1 初始化 Len[]={INFINITE , 0 , INFINITE , 10, INFINITE , 30 , 100} 这里数组首元素未用到,数组下标从1开始表示V0以此类推
2.第一次循环与V0相邻的有V2、V4、V5,其中V2距离最短为10,标记V2,并且以V2为中间点(路径为V0->V2->Vx)更新最短路表,此时V3被更新为10+50=60,。
3.进入第二次循环,此时未被标记的有V1、V3、V4、V5,,其中从V0到这些的临时最短路分别为INFINITE、60、30、100,从中找到最小的即V4,将V4标记为1,以V4为中间点(路径为V0->V4->Vx)更新最短路表,此时V3被更新为50,V5被更新为90。
4.进入第三次循环,此时未被标记的有V1、V3、V5,其中临时最短路分别为INFINITE、50、90,从中找到最小的即V3,将V3标记为1,以V3为中间点(路径为V0->V4->V3->Vx)更新最短路表,此时V5被更新成60。
5.进入第四次循环,此时未被标记的有V1、V5,其中临时最短路分别为INFINITE、60,找到V5,标记为1,以V5为中间点更新最短路表,此时没有元素被更新
6.进入第五次循环,这次循环没找到任何东西
7.退出循环,Len表中即为V0到其余各个节点的最短路径。
以上就是Dijkstra算法最基本的思想,当然,在找最短路时我们常常会需要求出到达某点的最短路径,那么下面,我们就来看看要怎样记录下到达某点的最短路径:
在Dijkstra算法的前提下加入查询最短路径其实很简单,只要在每次更新最短路时保存在该顶点的父节点序号即可,最后输出时回退中间节点然后用堆栈输出即可
最后直接给出完整代码(写的很一般,还望指教):
<span style="font-size:32px;color:#3333ff;">#include <stdio.h>
#include <string.h>
#define MAX_LEN 100
#define INFINITE 1000
typedef struct graph
{
int nodenum;
int edgenum;
int matrix[MAX_LEN][MAX_LEN];
}Graph;
typedef struct stack
{
int bottom;
int top;
int printout[MAX_LEN];
}mstack;
int in[MAX_LEN];
int Len[MAX_LEN];
int path[MAX_LEN];
void InitStack(mstack *s)
{
s->bottom=0;
s->top=0;
memset(s->printout,0,sizeof(int)*MAX_LEN);
}
void push(mstack *s,int m)
{
s->printout[s->top++]=m;
}
int pop(mstack *s)
{
return s->printout[--s->top];
}
void InitGraph(Graph *g,int n)
{
int i,j;
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
{
if(i==j)g->matrix[i][j]=0;
else g->matrix[i][j]=INFINITE;
}
for(i=1;i<=n;i++)
{
in[i]=0;
Len[i]=INFINITE;
path[i]=0;
}
}
int main()
{
int n,m,i,A,B,templen,count,min,tempmin,si,temp;
while(scanf("%d %d",&n,&m))
{
count=0;
Graph mGraph;
mGraph.edgenum=m;
mGraph.nodenum=n;
InitGraph(&mGraph,n);
for(i=0;i<m;i++)
{
scanf("%d %d %d",&A,&B,&templen);
mGraph.matrix[A][B]=templen;
}
in[1]=1;
path[1]=1; //sava path
Len[1]=0;
for(i=2;i<=n;i++)
{
Len[i]=mGraph.matrix[1][i]; //Init the len
if(Len[i]!=INFINITE)path[i]=1;
}
min=0;
si=1;
while(count<n-1)
{
tempmin=INFINITE;
for(i=1;i<=n;i++)
{
if(in[i]==0&&Len[i]<tempmin) //find the smallest one
{
tempmin=Len[i];
si=i;
}
}
in[si]=1;
for(i=1;i<=n;i++) //updata the length
{
if(in[i]==0&&(tempmin+mGraph.matrix[si][i])<Len[i])
{
Len[i]=tempmin+mGraph.matrix[si][i];
path[i]=si;
}
}
count++;
}
mstack s;
for(i=1;i<=n;i++)
{
temp=i;
InitStack(&s);
if(path[temp]==0)
{
printf("no path\n");
continue;
}
while(path[temp]!=1)
{
push(&s,path[temp]);
temp=path[temp];
}
printf("1-->");
while(s.bottom!=s.top)
{
printf("%d-->",pop(&s));
}
printf("%d min length is %d\n",i,Len[i]);
}
}
return 0;
}</span>
附上上面那张图的结果(V0节点为1,V1节点为2.。。。以此类推)
====================================================================
Dijkstra算法
1.定义概览
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法是很有代表性的最短路径算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。注意该算法要求图中不存在负权边。
问题描述:在无向图 G=(V,E) 中,假设每条边 E[i] 的长度为 w[i],找到由顶点 V0 到其余各点的最短路径。(单源最短路径)
2.算法描述
1)算法思想:设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
2)算法步骤:
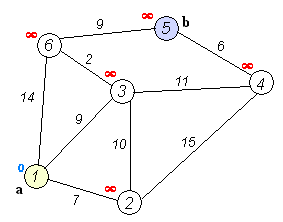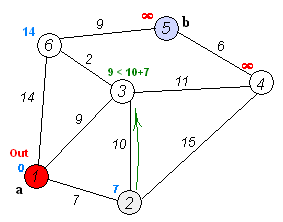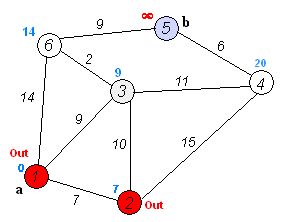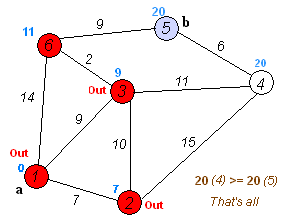
a.初始时,S只包含源点,即S={v},v的距离为0。U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u有边,则<u,v>正常有权值,若u不是v的出边邻接点,则<u,v>权值为∞。
b.从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
c.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
d.重复步骤b和c直到所有顶点都包含在S中。
执行动画过程如下图
3.算法代码实现:
const int MAXINT = 32767; const int MAXNUM = 10; int dist[MAXNUM]; int prev[MAXNUM]; int A[MAXUNM][MAXNUM]; void Dijkstra(int v0) { bool S[MAXNUM]; // 判断是否已存入该点到S集合中 int n=MAXNUM; for(int i=1; i<=n; ++i) { dist[i] = A[v0][i]; S[i] = false; // 初始都未用过该点 if(dist[i] == MAXINT) prev[i] = -1; else prev[i] = v0; } dist[v0] = 0; S[v0] = true; for(int i=2; i<=n; i++) { int mindist = MAXINT; int u = v0; // 找出当前未使用的点j的dist[j]最小值 for(int j=1; j<=n; ++j) if((!S[j]) && dist[j]<mindist) { u = j; // u保存当前邻接点中距离最小的点的号码 mindist = dist[j]; } S[u] = true; for(int j=1; j<=n; j++) if((!S[j]) && A[u][j]<MAXINT) { if(dist[u] + A[u][j] < dist[j]) //在通过新加入的u点路径找到离v0点更短的路径 { dist[j] = dist[u] + A[u][j]; //更新dist prev[j] = u; //记录前驱顶点 } } } }
4.算法实例
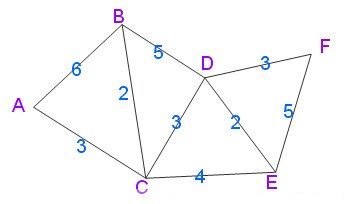
先给出一个无向图
用Dijkstra算法找出以A为起点的单源最短路径步骤如下
Floyd算法
1.定义概览
Floyd-Warshall算法(Floyd-Warshall algorithm)是解决任意两点间的最短路径的一种算法,可以正确处理有向图或负权的最短路径问题,同时也被用于计算有向图的传递闭包。Floyd-Warshall算法的时间复杂度为O(N3),空间复杂度为O(N2)。
2.算法描述
1)算法思想原理:
Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话,首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题,我们需要为这个目标重新做一个诠释(这个诠释正是动态规划最富创造力的精华所在)
从任意节点i到任意节点j的最短路径不外乎2种可能,1是直接从i到j,2是从i经过若干个节点k到j。所以,我们假设Dis(i,j)为节点u到节点v的最短路径的距离,对于每一个节点k,我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立,如果成立,证明从i到k再到j的路径比i直接到j的路径短,我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j),这样一来,当我们遍历完所有节点k,Dis(i,j)中记录的便是i到j的最短路径的距离。
2).算法描述:
a.从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。
b.对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。
3).Floyd算法过程矩阵的计算----十字交叉法
方法:两条线,从左上角开始计算一直到右下角 如下所示
给出矩阵,其中矩阵A是邻接矩阵,而矩阵Path记录u,v两点之间最短路径所必须经过的点
相应计算方法如下:
最后A3即为所求结果
3.算法代码实现
typedef struct { char vertex[VertexNum]; //顶点表 int edges[VertexNum][VertexNum]; //邻接矩阵,可看做边表 int n,e; //图中当前的顶点数和边数 }MGraph; void Floyd(MGraph g) { int A[MAXV][MAXV]; int path[MAXV][MAXV]; int i,j,k,n=g.n; for(i=0;i<n;i++) for(j=0;j<n;j++) { A[i][j]=g.edges[i][j]; path[i][j]=-1; } for(k=0;k<n;k++) { for(i=0;i<n;i++) for(j=0;j<n;j++) if(A[i][j]>(A[i][k]+A[k][j])) { A[i][j]=A[i][k]+A[k][j]; path[i][j]=k; } } }
算法时间复杂度:O(n3)
=========================================================================
Dijkstra(迪杰斯特拉)算法是典型的最短路径路由算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。
Dijkstra算法是很有代表性的最短路算法,在很多专业课程中都作为基本内容有详细的介绍,如数据结构,图论,运筹学等等。
其基本思想是,设置顶点集合S并不断地作贪心选择来扩充这个集合。一个顶点属于集合S当且仅当从源到该顶点的最短路径长度已知。
初始时,S中仅含有源。设u是G的某一个顶点,把从源到u且中间只经过S中顶点的路称为从源到u的特殊路径,并用数组dist记录当前每个顶点所对应的最短特殊路径长度。Dijkstra算法每次从V-S中取出具有最短特殊路长度的顶点u,将u添加到S中,同时对数组dist作必要的修改。一旦S包含了所有V中顶点,dist就记录了从源到所有其它顶点之间的最短路径长度。
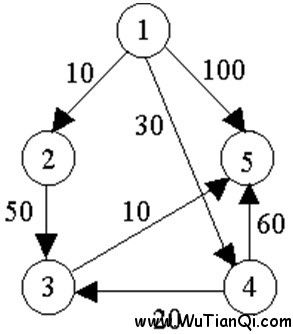
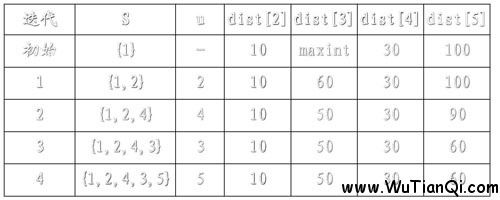
例如,对下图中的有向图,应用Dijkstra算法计算从源顶点1到其它顶点间最短路径的过程列在下表中。
主题好好理解上图!
以下是具体的实现(C/C++):
#include <iostream>
#include<fstream>
using namespace std;
const int maxnum = 100;
const int maxint = 999999;
void Dijkstra(int n, int v, int *dist, int *prev, int c[maxnum][maxnum])
{
bool s[maxnum]; // 判断是否已存入该点到S集合中
for(int i=1; i<=n; ++i)
{
dist[i] = c[v][i];
s[i] = 0; // 初始都未用过该点
if(dist[i] == maxint)
prev[i] = 0;
else
prev[i] = v;
}
dist[v] = 0;
s[v] = 1;
// 依次将未放入S集合的结点中,取dist[]最小值的结点,放入结合S中
// 一旦S包含了所有V中顶点,dist就记录了从源点到所有其他顶点之间的最短路径长度
for(i=2; i<=n; ++i)
{
int tmp = maxint;
int u = v;
// 找出当前未使用的点j的dist[j]最小值
for(int j=1; j<=n; ++j)
if((!s[j]) && dist[j]<tmp)
{
u = j; // u保存当前邻接点中距离最小的点的号码
tmp = dist[j];
}
s[u] = 1; // 表示u点已存入S集合中
// 更新dist
for( j=1; j<=n; ++j)
if((!s[j]) && c[u][j]<maxint)
{
int newdist = dist[u] + c[u][j];
if(newdist < dist[j])
{
dist[j] = newdist;
prev[j] = u;
}
}
}
}
void searchPath(int *prev,int v, int u)
{
int que[maxnum];
int tot = 1;
que[tot] = u;
tot++;
int tmp = prev[u];
while(tmp != v)
{
que[tot] = tmp;
tot++;
tmp = prev[tmp];
}
que[tot] = v;
for(int i=tot; i>=1; --i)
if(i != 1)
cout << que[i] << " -> ";
else
cout << que[i] << endl;
}
int main()
{
freopen("input.txt", "r", stdin);
// 各数组都从下标1开始
int dist[maxnum]; // 表示当前点到源点的最短路径长度
int prev[maxnum]; // 记录当前点的前一个结点
int c[maxnum][maxnum]; // 记录图的两点间路径长度
int n, line; // 图的结点数和路径数
// 输入结点数
cin >> n;
// 输入路径数
cin >> line;
int p, q, len; // 输入p, q两点及其路径长度
// 初始化c[][]为maxint
for(int i=1; i<=n; ++i)
for(int j=1; j<=n; ++j)
c[i][j] = maxint;
for(i=1; i<=line; ++i)
{
cin >> p >> q >> len;
if(len < c[p][q]) // 有重边
{
c[p][q] = len; // p指向q
c[q][p] = len; // q指向p,这样表示无向图
}
}
for(i=1; i<=n; ++i)
dist[i] = maxint;
for(i=1; i<=n; ++i)
{
for(int j=1; j<=n; ++j)
printf("%8d", c[i][j]);
printf("\n");
}
Dijkstra(n, 1, dist, prev, c);
// 最短路径长度
cout << "源点到最后一个顶点的最短路径长度: " << dist[n] << endl;
// 路径
cout << "源点到最后一个顶点的路径为: ";
searchPath(prev, 1, n);
return 0;
}
/*
输入数据:
5
7
1 2 10
1 4 30
1 5 100
2 3 50
3 5 10
4 3 20
4 5 60
输出数据:
999999 10 999999 30 100
10 999999 50 999999 999999
999999 50 999999 20 10
30 999999 20 999999 60
100 999999 10 60 999999
源点到最后一个顶点的最短路径长度: 60
源点到最后一个顶点的路径为: 1 -> 4 -> 3 -> 5
*/
最短路
Time Limit: 5000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 13799 Accepted Submission(s): 5874
#include<iostream> #include<stdio.h> #include<iomanip> using namespace std; #define N 10000 #define MAX 100000099 int a[N][N]; int dist[N]; void input (int n,int m) { int p,q,len,i,j; for( i=1;i<=n;i++) { for(j=1;j<=n;j++) a[i][j]=MAX; dist[i]=MAX; } for(i=0;i<m;i++) { cin>>p>>q>>len; if(len<a[p][q]) { a[p][q]=len; a[q][p]=len; } } } void dijkstra(int n) { int s[N],newdist; for(int i=1;i<=n;i++) { dist[i]=a[1][i]; s[i]=0; } dist[1]=0; s[1]=1; for(i=2;i<=n;i++) { int j,tem=MAX; int u=1; for(j=2;j<=n;j++) if(!s[j]&&dist[j]<tem) { u=j; tem=dist[j]; } s[u]=1; for(j=2;j<=n;j++) { if(!s[j]&&a[u][j]<MAX) { newdist=dist[u]+a[u][j]; if(newdist<dist[j]) dist[j]=newdist; } } } } int main() { int n,m; while(scanf("%d%d",&n,&m),m||n) { input(n,m); dijkstra(n); cout<<dist[n]<<endl; } return 0; }
//又捡回来了 #include <iostream> #include<string.h> using namespace std; const int Nmax = 104; int a[Nmax][Nmax]; bool visit[Nmax]; int prev[Nmax]; int n; void dijkstra(int v)//不需要打印路径的dijkstra { int cnt=n-1,j,mindis,minid; memset(visit,0,sizeof(visit)/sizeof(bool)); for(j=1; j<=n; j++) { if(a[v][j]==INT_MAX||v==j) prev[j]=0; //路径打印停止的标志 else prev[j]=v; } visit[v]=1; while(cnt--) //n-1次就可以将所有定点加入S中 { //找到距离v点最近的点k mindis=INT_MAX; for(j=1; j<=n; j++) { if(!visit[j]&&a[v][j]<mindis) { mindis=a[v][j]; minid=j; } } visit[minid]=1; //更新集合U中的点 for(j=1; j<=n; j++) { //a[v][minid]+a[minid][j]<a[v][j]会溢出尼玛!!装逼失败早知道不用INT_MAX if(!visit[j]&&a[v][minid]<INT_MAX&&a[minid][j]<INT_MAX&&a[v][minid]+a[minid][j]<a[v][j]) { a[v][j]=a[v][minid]+a[minid][j]; prev[j]=minid; } } } } void printPath(int u) { int path[Nmax]; int tmp=u; while(tmp) { path[prev[tmp]]=tmp; tmp=prev[tmp]; } while(tmp!=u) { cout<<path[tmp]; tmp=path[tmp]; if(tmp!=u) cout<<"->"; } cout<<endl; }int main() { int i,j,w,m; while(cin>>n>>m,n||m) { for(i=1; i<=n; i++) for(j=1; j<=n; j++) { if(i==j) a[i][j]=0; else a[i][j]=INT_MAX; } while(m--) { cin>>i>>j>>w; //a[i][j]=w<a[i][j]?w:a[i][j];有向图重边考虑 a[i][j]=a[j][i]=w<a[i][j]?w:a[i][j];//无向图重边考虑 } dijkstra(1); cout<<a[1][n]<<endl; //printPath(n); } return 0; }