模式识别中Fisher分类器的Matlab实现及测试

Fisher分类器用于解决二类线性可分问题。

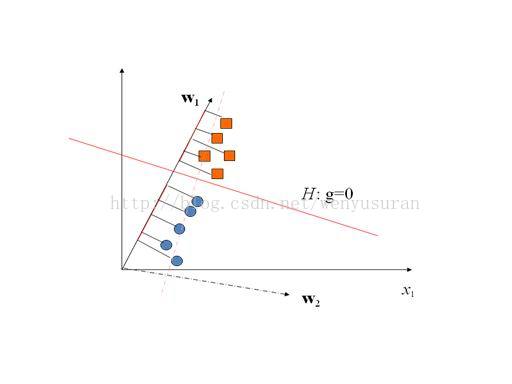
Fisher准则基本原理：找到一个最合适的投影轴，使两类样本在该轴上投影之间的距离尽可能远，而每一类样本的投影尽可能紧凑，从而使分类效果为最佳。

例如上图中：通过将方块点和圆点向w1投影，然后再在设置合适的阈值即可将方块和圆点分离。

 

Matlab程序如下：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%By Shelley from NCUT，April 2nd 2011
%Email:[email protected]
%本m文件实现fisher算法，并对两个二维正态分布随机序列
%进行训练，进而可在屏幕上任意取点，程序可输出属于第一类
%还是第二类
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%分别产生x轴和y轴都为正态分布的随机序列
%假设x轴和y轴序列相互独立，可产生二维正态分布随机序列
%w1、w2分别用来保存两个训练集的横坐标和纵坐标
%用normrnd函数产生正态分布函数
%normrnd（mean,omega,[row,column]）
%mean:均值;omega:标准差
%row:产生随机序列的行数;column:产生随机序列的列数
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 X1 = normrnd(40,10,[200,1]);
 Y1 = normrnd(40,10,[200,1]);
 w1=[X1, Y1];
 X2 = normrnd(5 ,10,[100,1]);
 Y2 = normrnd(0 ,10,[100,1]);
 w2=[X2, Y2];
 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%以下部分为fisher算法的实现
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%计算样本均值
m1=mean(w1)';
m2=mean(w2)';
%s1、s2分别代表表示第一类、第二类样本的类内离散度矩阵
s1=zeros(2);
[row1,colum1]=size(w1);
for i=1:row1
    s1 = s1 + (w1(i,:)'-m1)*(w1(i,:)'-m1)';
end;
s2=zeros(2);
[row2,colum2]=size(w2);
for i=1:row2
    s2 = s2 + (w2(i,:)' - m2)*(w2(i,:)' - m2)';
end;
%计算总类内离散度矩阵Sw
Sw=s1+s2;
%计算fisher准则函数取极大值时的解w
w=inv(Sw)*(m1-m2);
%计算阈值w0
ave_m1 = w'*m1;
ave_m2 = w'*m2;
w0 = (ave_m1+ave_m2)/2;
%画出两类训练样本点
figure(1)
plot(X1,Y1,'.r',X2,Y2,'.b');%画出两类样本点
hold on;grid;
%画出取极大值时的解w
x = [-40:0.1:40];
y = x*w(2)/w(1);
plot(x,y,'g')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%以下为测试部分
%利用ginput随机选取屏幕上的点（可连续取10个点）
%程序可根据点的位置自动地显示出属于那个类
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:10
 

  [x,y]=ginput(1);
   plot(x,y,'m*');
   sample=[x,y];
    holdall
    if(sample*w- w0>0)
        disp('it belong to the first class');
    else
        disp('it belong to the second class');
    end;
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

代码二：

function fisher
x1=[0.2331 1.5207 0.6499 0.7757 1.0524 1.1974
    0.2908 0.2518 0.6682 0.5622 0.9023 0.1333
    -0.5431 0.9407 -0.2126 0.0507 -0.0810 0.7315
    0.3345 1.0650 -0.0247 0.1043 0.3122 0.6655
    0.5838 1.1653 1.2653 0.8137 -0.3399 0.5152
    0.7226 -0.2015 0.4070 -0.1717 -1.0573 0.2099];
x2=[2.3385 2.1946 1.6730 1.6365 1.7844 2.0155
    2.0681 2.1213 2.4797 1.5118 1.9692 1.8340
    1.8704 2.2948 1.7714 2.3939 1.5648 1.9329
    2.2027 2.4568 1.7523 1.6991 2.4883 1.7259
    2.0466 2.0226 2.3757 1.7987 2.0828 2.0798
    1.9449 2.3801 2.2373 2.1614 1.9235 2.2604];
x3=[0.5338 0.8514 1.0831 0.4164 1.1176 0.5536
    0.6071 0.4439 0.4928 0.5901 1.0927 1.0756
    1.0072 0.4272 0.4353 0.9869 0.4841 1.0992
    1.0299 0.7127 1.1024 0.4576 0.8544 1.1275
    0.7705 0.4129 1.0085 0.7676 0.8418 0.8784
    0.9751 0.7840 0.4158 1.0315 0.7533 0.9548];
%将x1,x2,x3变为列向量
x1=x1(:);
x2=x2(:);
x3=x3(:);
%计算第一类的样本均值向量
m1(1)=mean(x1);
m1(2)=mean(x2);
m1(3)=mean(x3);
%计算第一类样本类内散度矩阵S1
S1=zeros(3,3);
for i=1:36
    S1=S1+[-M1(1)+X1(I)-m1(2)+x2(i)-m1(3)+x3(i)]'*[-m1(1)+x1(i)-m1(2)+x2(i)-m1(3)+x3(i)];
end
x4=[1.4010 1.2301 2.0814 1.1655 1.3740 1.1829
    1.7632 1.9739 2.4152 2.5890 2.8472 1.9539
    1.2500 1.2864 1.2614 2.0071 2.1831 1.7909
    1.3322 1.1466 1.7087 1.5920 2.9353 1.4664
    2.9313 1.8349 1.8340 2.5096 2.7198 2.3148
    2.0353 2.6030 1.2327 2.1465 1.5673 2.9414];
x5=[1.0298 0.9611 0.9154 1.4901 0.8200 0.9399
    1.1405 1.0678 0.8050 1.2889 1.4601 1.4334
    0.7091 1.2942 1.3744 0.9387 1.2266 1.1833
    0.8798 0.5592 0.5150 0.9983 0.9120 0.7126
    1.2833 1.1029 1.2680 0.7140 1.2446 1.3392
    1.1808 0.5503 1.4708 1.1435 0.7679 1.1288];
x6=[0.6210 1.3656 0.5498 0.6708 0.8932 1.4342
    0.9508 0.7324 0.5784 1.4943 1.0915 0.7644
    1.2159 1.3049 1.1408 0.9398 0.6197 0.6603
    1.3928 1.4084 0.6909 0.8400 0.5381 1.3729
    0.7731 0.7319 1.3439 0.8142 0.9586 0.7379
    0.7548 0.7393 0.6739 0.8651 1.3699 1.1458];
x4=x4(:);
x5=x5(:);
x6=x6(:);
%计算第二类的样本均值向量m2
m2(1)=mean(x4);
m2(2)=mean(x5);
m2(3)=mean(x6);
%计算第二类样本类内散度矩阵S2
S2=zeros(3,3);
for i=1:36
    S2=S2+[-m2(1)+x4(i)-m2(2)+x5(i)-m2(3)+x6(i)]'*[-m2(1)+x4(i)-m2(2)+x5(i)-m2(3)+x6(i)];
end
%总类内散度矩阵
Sw=zeros(3,3);
Sw=S1+S2;
%样本类间散度矩阵Sb
Sb=zeros(3,3);
Sb=(m1-m2)'*(m1-m2);
%最优解W
W=S^-1*(m1-m2)'
%将W变为单位向量以方便计算投影
W=W/sqrt(sum(W.^2));
%计算一维Y空间中的各类样本均值M1及M2
for i=1:36
    y(i)=W'*[x1(i) x2(i) x3(i)]';
end
M1=mean(y)
for i=1:36
    y(i)=W'*[x4(i) x5(i) x6(i)]';
end
M2=mean(y)
%利用当P(w1)与P（w2）已知的公式计算wo
p1=0.6;p2=0.4;
W0=-(M1+M2)/2+(log(p2/p1))/(36+36-2);
%计算将样本投影到最佳方向上以后的新坐标
X1=[x1*W(1)+x2*W(2)+x3*W(3)]';
X2=[x4*W(1)+x5*W(2)+x6*W(3)]';%计算投影得到的长度
XX1=[W(1)*X1;W(2)*X1;W(3)*X1];
XX2=[W(1)*X2;W(2)*X2;W(3)*X2];%得到新坐标
%绘制样本点
figure(1)
plot3(x1,x2,x3,'r*') %第一类
hold on
plot3(x4,x5,x6,'bp') %第二类
legend('第一类点','第二类点')
title('Fisher线性判别函数')
W1=5*W;
%画出最佳方向
line([-W1(1),W1(1)],[-W1(2),W1(2)],[-W1(3),W1(3)],'color','b');
%判别已给点的分类
a1=[1,1,5,0.6]';
a2=[1.2,1.0,0.55]';
a3