编程之美 - 一排石头游戏及扩展问题
问题:一堆石头排成一排,两个人轮流从其中抓取一块或两块石头(两块石头必须是挨着的),谁拿到了最后的石头,谁就是赢家,编写算法保证先抓的人一定能赢。
思路:
假设有三块石头,甲先拿中间的
一块,这样无论乙怎么拿甲都会赢。
如果有四块石头,甲先拿中间的
两块,这样无论乙怎么拿甲也会赢。
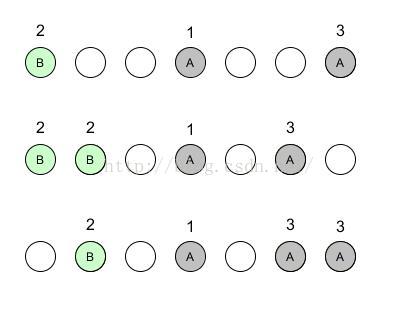
再扩展一下,如果有五块石头,甲先拿中间的一块,如果下面乙拿一块,甲就拿和乙中心对称的一块,这样甲还是会赢。
规律就是如果是奇数块石头,先拿的就拿中间的一块;如果是偶数块先拿的就先拿中间的两块。剩下的只要和对方的基于中心点对称就一定会赢。
程序实现:
#include <iostream>
using namespace std;
bool take_stone(char *stones, int len, int start, int num)
{
bool bRet = true;
if ((start < 0) || ((start+num) > len) || (num < 1 || num > 2))
return false;
if (((num == 1) && (stones[start] != 'O'))
|| ((num == 2) && ((stones[start] != 'O') || (stones[start+1] != 'O'))))
return false;
if (num == 1)
stones[start] = 'x';
else if (num == 2)
{
stones[start] = 'x'; stones[start+1] = 'x';
}
return bRet;
}
bool scan(char *stones, int len, int start, int num, int round)
{
int i = 0, mid = 0;
bool bRet = false;
mid = (len+1)/2;
if (round == 0)
{
if (len%2 == 1)
{
mid = (len-1)/2;
stones[mid] = 'x';
}
else
{
mid = len/2 - 1;
stones[mid] = 'x'; stones[mid+1] = 'x';
}
}
else
{
mid = len - 1 - start;
stones[mid] = 'x';
mid = mid - (num-1);
stones[mid] = 'x';
}
for (i=0; i < len; i++)
{
if (stones[i] == 'O')
{
bRet = true;
break;
}
}
if (!bRet)
{
cout << "PROGRAM WIN!!" << endl;
bRet = false;
}
return bRet;
}
void print(char *stones, int len)
{
int i = 0;
for (i=0; i < len; i++)
{
cout << stones[i] << " ";
}
cout << endl;
}
void play(char *stones, int len)
{
int nStart=0, nNum=0;
int round = 0;
while(scan(stones, len, nStart, nNum, round))
{
print(stones, len);
cout << "please input the start stone and will take how many(max is 2)" << endl;
cin >> nStart >> nNum;
while (!take_stone(stones, len, nStart, nNum))
{
cout << "please re-input your choose" <<endl;
cin >> nStart >> nNum;
}
round++;
}
print(stones, len);
}
void main()
{
char test[]={'O','O','O','O','O','O','O','O'};
int len = 8;
play(test, len);
cin >> len;
}
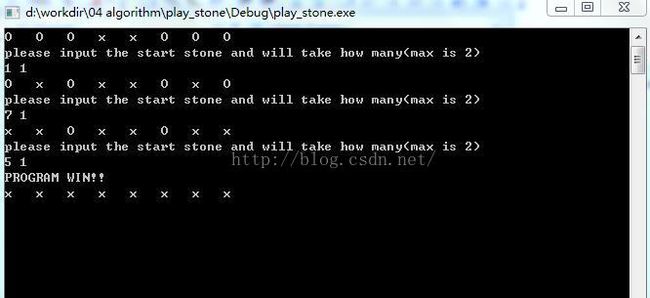
测试结果:
---------------------------------------------------------------------------------------------------------------------------------------------------
---------------------------------------------------------------------------------------------------------------------------------------------------
扩展问题
,如果把规则变为抓到最后一个石头的人输呢?
思路:
还是从头开始一块,两块的开始分析
1 块: 先抓必输 把这种情况定义为 0
First Lose
FL
2 块: 先抓必赢 把这种情况定义为 1
First Win
FW
3 块: 先抓必赢
FW
4 块:
1 + 3 先抓 1 块,剩3块,那后抓的人一定会赢 FL
2 + 2 先抓 2 块,剩2块,那后抓的人一定会赢
---------------------------------------------------------------------------------------------------------------------------------------------------
前三种情况很明显,从第 5 块开始需要分解
5 块:
A可以选择取一块或取两块
那么
取完 1 块后
,B可能面临的情况:
1) 4 B 输
2) 1 || 3 B 赢
3) 2 || 2 B 输
那么取完
2
块后,B可能面临的情况:
4) 3 B 赢
5) 1 || 2 B 赢
A可以选择方案 1 或 3 必胜
6 块:
那么
取完 1 块后,B可能面临的情况:
1) 5
B 赢
2) 1 || 4 B 赢
3) 2 || 3
B 赢
那么
取完
2
块后,B可能面临的情况:
4) 4 B 输
5) 1 || 3 B 赢
6) 2 || 2
B 输
A可以选择方案 4 或 6
必胜
7 块:
那么
取完 1 块后,B可能面临的情况:
1) 6
B 赢
2) 1 || 5 B 输
3) 2 || 4
B
赢
4) 3 || 3
B
输
那么
取完
2
块后,B可能面临的情况:
5) 5
B 赢
6)
1 || 4
B
赢
7)
2 || 3
B
赢
A可以选择方案 2 或 4
必胜
8 块:
那么
取完 1 块后,B可能面临的情况:
1) 7
B 赢
2) 1 || 6 B
赢
3) 2 || 5
B
赢
4) 3 || 4
B
输
那么
取完
2
块后,B可能面临的情况:
5) 6
B 赢
6)
1 || 5
B
输
7)
2 || 4
B
赢
8)
3 || 3
B
输
A可以选择方案 4,6,8
必胜
9 块:
那么
取完 1 块后,B可能面临的情况:
1) 8
B 赢
2) 1 || 7 B
赢
3) 2 || 6
B
赢
4) 3 || 5
B
赢
5) 4 || 4 B 赢
那么
取完
2
块后,B可能面临的情况:
6) 7
B 赢
7)
1 || 6
B
赢
8)
2 || 5
B
赢
9)
3 || 4
B
赢
当 9块石头时A
一定会输
因为当 N = 4 或 9时先取的一定会输,N = 5,6,7,8先取一定会赢
可以看出基于这个规则,先取无法保证一定会赢。
总结一下规律
规律 1:
对于目标数字进行分解,如果发现
分解后的一个组合可以让对方必输的,则可以把当前的分解看做是
先手必胜的。
如果,发现一个数字的
所有分解都是
FW(first win) 的,那当前这个组合是
必输的。例如 9,分解后都是对方赢的,那面对 9 时就是必输的了。
规律 2:
1:N ==> 有奇数个1时先取的输,偶数时先取的赢
2:N ==> 有奇数个key时先取的赢,偶数时先取的输
当1 和 2 有组合时
1 || 2 ==> FW
1 || 1 || 2 ==> FW
1 || 2 || 2 ==> FW
1 || 1 || 2 || 2 ==> FL
1 || 2 || 2 || 2 ==> FW
1 || 1 || 2 || 2 || 2 ==> FW
当有
奇数个2时,不用考虑 1 的个数,
先手都会
赢。
当有
偶数个2时,如果有奇数个 1,
先手会
赢。
当有
偶数个2时,如果有偶数个 1,
后手会
赢。
算法描述:
1)扫描当前石头情况,得到当前分解的情况:
例如:
O O O O O : seq = 5
O X O O O : seq = 1 | | 3
2)如果当前分解中有大于 2 的数字就需要继续分解得到子序列,此处需要用到递归
例如:
O O O O O : seq = 5
可以分解为:
X O O O O : sub_seq = 0 || 4
O X O O O : sub_seq = 1 || 3
O O X O O : sub_seq = 2 || 2
4 和 1 || 3需要继续分解
3)当完全分解完全到位后,可根据上面的规律2可以知道它的序列是 FW(First Win) 或 FL(First Lose)
序列中没有大于2的数字
4)通过子序列的 FW和FL属性可以得父序列是 FW(First Win) 或 FL(First Lose)
- 如果子序列全是 FW,则父序列是 FL
- 如果子序列中有一个是FL,则父序列是 FW
5)当得到最原始序列的FW(First Win) 或 FL(First Lose)属性后,如果是FW则自己先选,如果是FL的则可以让对手先选