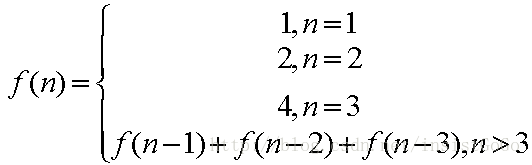每日一题(30)- 斐波那契数列以及应用
题目来自剑指offer
题目:
说明:
形成的斐波那契数列为:0,1,2,3,5,8...
思路:
可以直接使用递归,但是有重复子问题。可以使用迭代。
递归代码:
long Fibonacci(unsigned int n)
{
if (n == 1)
{
return 1;
}
if (n == 2)
{
return 2;
}
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
迭代代码:
long Fibonacci(long n)
{
long One = 1;
long Two = 2;
long Sum = 0;
for (long i = 3;i <= n;i++)
{
Sum = One + Two;
One = Two;
Two = Sum;
}
return Sum;
}
斐波那契数列的应用
1、兔子繁殖问题
2、矩形覆盖问题
3、青蛙跳台阶问题
---------------------------------------------
1、兔子繁殖问题
题目:兔子在出生两个月后,就有繁殖能力,一对兔子每个月能生出一对小兔子(一公一母)来。如果所有兔子都不死,那么一年以后可以繁殖多少对兔子?
思路:详细见百度百科:斐波那契数列
2、矩形覆盖问题
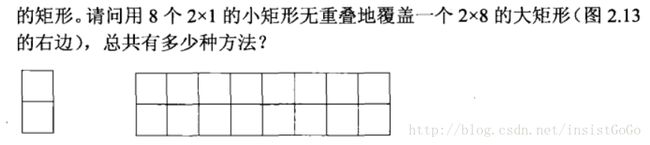
题目:
分析:
假设f(n)表示覆盖2 * n的矩形的总放法,其中2表示行,n表示列,我们要求f(8)。
f(1):只有一种方法。就是找一个2*1的矩形竖着放
f(2):两种方法,找两个2*1矩形竖着放,或者两个2*1矩形横着放
f(3):三种方法,找三个2*1矩形都是竖着放(一种),找一个2*1矩形竖着放,两个2*1矩形竖着放(2种)
。。。之后会发现是一个斐波那契数列。。。
3、青蛙跳台阶问题
题目(1):一个台阶总共有n级,一个青蛙一次可以跳1级,也可以跳2级。求青蛙跳上n级台阶总共有多少总跳法?
分析:
如果只有1个台阶,那么只有一种跳法;
如果只有2级台阶,那么有2种跳法。
对于一个n级台阶的楼梯来说,设跳法为 f(n) :
假如我们先跳1个台阶,则剩下有 n-1 个台阶,跳法为 f(n-1) 次,
假如我们先跳2个台阶,则剩下 n-2 阶,跳法为 f(n-2);
由此可以推出,对于一个n阶的楼梯,有以下这个跳台阶的公式:
题目(2):一个台阶总共有n级,一个青蛙一次可以跳1级,也可以跳2级,也可以跳三级。求青蛙跳上n级台阶总共有多少总跳法?
分析:
如果只有1个台阶,那么只有一种跳法;
如果只有2级台阶,那么有2种跳法。
如果只有3级台阶,那么有4种跳法。
对于一个n级台阶的楼梯来说,设跳法为 f(n) :
假如我们先跳1个台阶,则剩下有 n-1 个台阶,跳法为 f(n-1) 次,
假如我们先跳2个台阶,则剩下 n-2 阶,跳法为 f(n-2);
假如我们先跳3个台阶,则剩下 n-3 阶,跳法为 f(n-3);
由此可以推出,对于一个n阶的楼梯,有以下这个跳台阶的公式:
题目(3):一个台阶总共有n级,一个青蛙一次可以跳1级,也可以跳2级......它也可以跳上n级。此时该青蛙跳上一个n级的台阶总共有多少种跳法?
分析:
如果只有1个台阶,那么只有一种跳法;(1)
如果只有2级台阶,那么有2种跳法。(1,1)(2)
如果只有3级台阶,那么有4种跳法。(1,1,1)(1,2)(2,1),(3)
对于一个n级台阶的楼梯来说,设跳法为 f(n) :
假如我们先跳1个台阶,则剩下有 n-1 个台阶,跳法为 f(n-1) 次,
假如我们先跳2个台阶,则剩下 n-2 阶,跳法为 f(n-2);
假如我们先跳3个台阶,则剩下 n-3 阶,跳法为 f(n-3);
....
假如我们先跳n - 1个台阶,则剩下1阶,跳法为 f(1);
假如我们先跳n个台阶,则剩下1阶,跳法为 f(0);
由此可以推出,对于一个n阶的楼梯,有以下这个跳台阶的公式:
f(n) = f(0) + f(1) + f(2) + ... +f(n - 1)
同理有:
f(n - 1) = f(0) + f(1) + f(2) + ... +f(n - 2)
两个式子作差得到
f(n) - f(n - 1) = f(n - 1)
即,f(n) = 2f(n - 1)
则递推式子为: